7.1: El concepto de energía potencial
- Page ID
- 85098
Desde la física de secundaria debes recordar dos ecuaciones
\[E = \frac{1}{2} Mv^2 \quad \text{ kinematic energy}\]
\[W = mgH \quad \text{ potential energy} \]
donde\(H\) es la altura de una masa\(m\) desde cierto nivel de referencia\(H_o\), y\(g\) representa la aceleración terrestre. El nivel de referencia podría ser el centro de la tierra, el nivel del mar o cualquier superficie a partir de la cual\(H\) se mida.
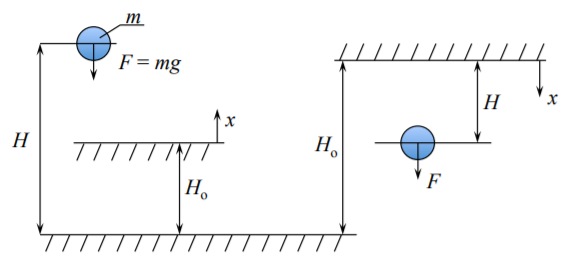
Rara vez medimos\(H\) desde el centro de la tierra. Por lo tanto, lo que podemos medir fácilmente es el cambio de la energía potencial
\[\Delta W = (mg)(H − H_o) \label{7.1.3}\]
La energía siempre es positiva. Puede e cero pero no puede ser negativo. La fuerza de gravedad\(F = mg\) se dirige hacia el centro de la tierra. Por lo tanto, existe la necesidad del signo negativo en la Ecuación\ ref {7.1.3}). En el sistema de coordenadas de la Figura (\(\PageIndex{1}\)), la fuerza de gravedad es negativa (opuesta al sentido de coordenada\(x\)). La fuerza\(F\) está actuando en el sentido de\(x\) pero la diferencia\(H − H_o\) es negativa.
Extendiendo el concepto de la energía potencial al haz, la fuerza es\(F = q dx\) y la\(w = H − H_o\) es la deflexión del haz.
\[W \equiv + \int_{0}^{l} qw dx \]
Una expresión análoga para las placas es
\[W \equiv + \int_{S} pw ds \]
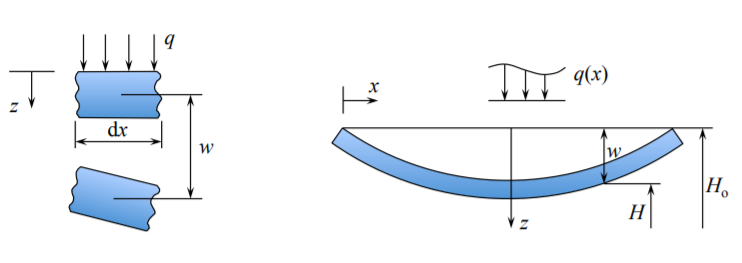
En la definición anterior\(W\) es negativa.
El concepto de la energía almacenada elásticamente se\(U\) ha introducido anteriormente. Para un cuerpo 3-D
\[U = \int_{V} \frac{1}{2} \sigma_{ij}\epsilon_{ij} dv \]
y para una viga
\[U = \int_{0}^{l} \frac{1}{2} MK dx + \int_{0}^{l} \frac{1}{2} N \epsilon^{\circ} dx \]
Para las placas, las energías de flexión y membrana están dadas por las Ecuaciones (3.6.25), (3.6.26) y (3.6.41), (3.6.42).
La energía potencial total\(\prod\) es un concepto nuevo, y se define como la suma de la energía de drenaje y la energía potencial
\[\prod = U + (−W) = U − W \]
Considera por un tiempo que el material es rígido, para lo cual\(U \equiv 0\). Imagínese que una bola rígida es desplazada por una cantidad infinitesimal sobre una\((\theta \neq 0)\) superficie plana\((\theta = 0)\) e inclinada, Figura (\(\PageIndex{3}\)).
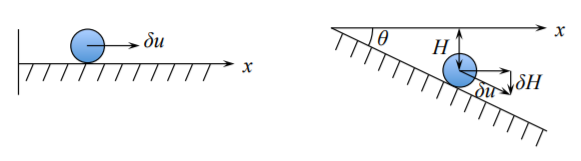
Tenemos\(H = u \sin \theta\) y\(\delta H = \delta u \sin \theta\). La energía potencial total y su cambio es
\[\prod = −W = −F u \sin \theta \]
\[\delta \prod = −\delta W = −(F \sin \theta) \delta u \]
En la superficie plana,\(\theta = 0\) y\(\delta \prod = 0\), y la pelota está en equilibrio estático (neutro). Si\(\theta > 0\),\(\delta \prod \neq 0\) y la pelota no está en equilibrio estático. Tenga en cuenta que si se agrega la fuerza de inercia d'Alambert en la dirección del movimiento, la pelota seguirá estando en equilibrio dinámico. En esta conferencia, sólo se considera el equilibrio estático. Ahora podemos extender la prueba de equilibrio anterior e introducir el siguiente principio:
Se dice que el sistema está en equilibrio, si un cambio infinitesimal del argumento\(a\) de la energía potencial total\(\prod = \prod(a)\) no cambia la energía potencial total
\[\delta \prod (a) = \frac{\partial \prod}{\partial a} \delta a = 0 \]
Porque\(\delta a \neq 0\) (\(\delta a = 0\)es un caso trivial en el que no se realiza ninguna prueba de equilibrio), la condición necesaria y suficiente para la estabilidad es
\[\frac{\partial \prod}{\partial a} = 0\]
En caso de que el funcional\(\prod\) sea una función de muchas (digamos\(N\)) variables\(\prod = \prod(a_i)\), el incremento
\[\delta \prod = \frac{\partial \prod}{\partial a_i} \delta a_i, \quad i = 1, \dots, N\]
El sistema está en equilibrio si la derivada de\(\prod\) con respecto a cada variable a la vez desaparece
\[\frac{\partial \prod (a_i)}{\partial a_i} = 0, \quad i = 1, \dots, N \]
A continuación se explicará el significado del argumento o argumentos\(a_i\), o variables independientes.


