7.6: Teorema de Castigliano
- Page ID
- 85103
Este teorema se aplica a estructuras y sistemas determinados estáticamente sometidos a fuerzas o momentos concentrados. La distribución de los momentos de flexión se puede determinar de manera única a partir del equilibrio global como función de las fuerzas,\(U = U(P)\). La energía potencial total es
\[\prod = U(P) − P w_o\]
Para una amplitud de deflexión dada\(w_o\), la magnitud de la carga se ajusta para hacer que la energía potencial total sea estacionaria. Matemáticamente
\[\delta [\prod (P)] = \delta [U(P) − P w_o] = \frac{dU}{dP} \delta P − w_o \delta P = \left[ \frac{dU(P)}{dP} − w_o \right] \delta P = 0\]
Hemos demostrado que el desplazamiento bajo la fuerza en la dirección de la fuerza es igual a la derivada de la energía elástica almacenada con respecto a la fuerza.
Para interpretar la propiedad estacionaria de\(\prod\), considere una viga en voladizo con la fuerza\(P\) en su punta. La distribución del momento de flexión es\(M(x) = P(l − x)\). Escojamos la formulación de fuerza de la energía potencial total, Ecuación (?? ). La energía potencial total es
\[[\prod = \frac{P^2}{2EI} \int_{0}^{l} (l − x)^2 dx − P w_o \label{8.49}\]
Después de la integración
\[\prod(P) = P \left( \frac{Pl^3}{6EI} − w_o \right) \]
La gráfica de esta función se muestra en la Fig (\(\PageIndex{1}\)).
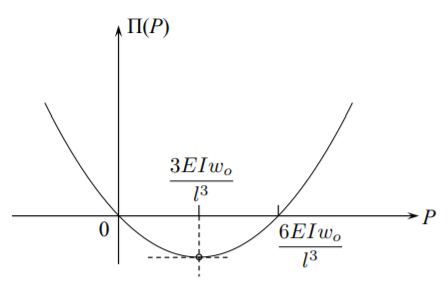
La parábola tiene dos raíces en\(P_1 = 0\) y en\(P_2 = \frac{6EIw_o}{l^3}\). El punto estacionario está en
\[P = \frac{3EIw_o}{l^3} \label{8.51}\]
que es la solución exacta del problema.
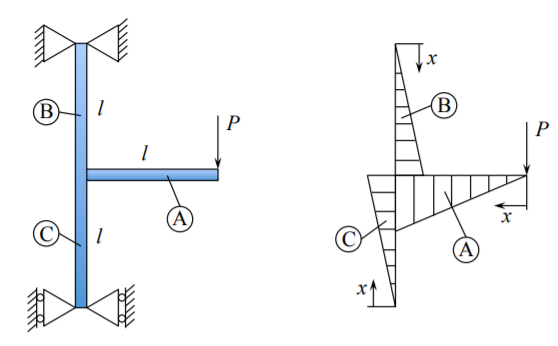
Como ilustración, considere dos sistemas estructurales simples. El primer sistema de dos vigas se muestra en la Figura (\(\PageIndex{2}\)).
Este problema se resolvió anteriormente utilizando desplazamientos y continuidad de taludes. Sigue una solución muy simple. Las distribuciones de momento de flexión son
\[\text{ Beam (A) } \; M(x) = −P x \; 0 < x < l \\ \text{ Beam (B) } \; M(x) = \frac{1}{2} P x \; 0 < x < l \\ \text{ Beam (C) } \; M(x) = − \frac{1}{2} P x \; 0 < x < l \]
La energía de deformación por flexión es
\[U(P) = \int_{0}^{l} \frac{1}{2EI} \left[ P^2 + \left(\frac{P}{2}\right)^2 + \left(\frac{P}{2}\right)^2 \right] x^2 dx = \frac{3}{2} P^2 \frac{l^3}{3} = \frac{1}{2} P^2 l^3 \]
De las contribuciones relativas de las tres vigas en la Ecuación (7.5.13), se observa que el voladizo horizontal contribuye dos veces a la deflexión de la punta en comparación con la viga vertical.
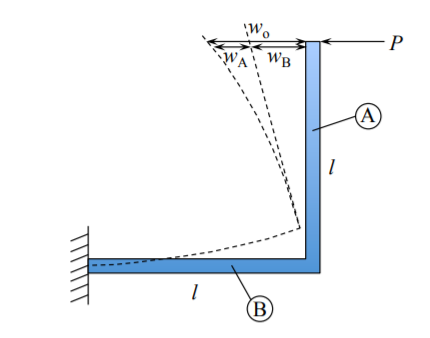
El segundo sistema consiste en un codo. De la Figura (\(\PageIndex{3}\)), la distribución del momento de flexión es
\[\text{ Beam (A) } \; M(x) = P x \\ \text{ Beam (B) } \; M(x) = Pl \]
La energía de flexión elástica del sistema es
\[U(P) = \frac{1}{2EI} \int_{0}^{l} (P x)^2 dx + \frac{1}{2EI} \int_{0}^{l} (P l)^2 dx = \frac{P^2}{2EI} \frac{4l^3}{3} \]
La deflexión total en la dirección de la fuerza es
\[w_o = \frac{dU}{dP} = \frac{4}{3} \frac{Pl^3}{EI} \]
Prueba del Teorema de Castigliano para un sistema de cargas puntuales,\(P_i\)
Los desplazamientos correspondientes se denotan por\(w_i\), ver Figura (\(\PageIndex{4}\)).
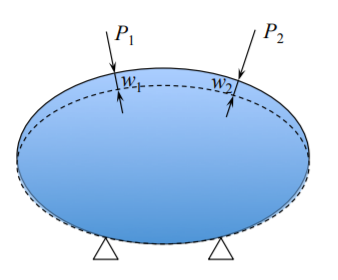
El trabajo de las fuerzas externas es
\[W = \sum_{i} P_iw_i = P_iw_i \]
Se supone que la energía almacenada puede expresarse en términos de todas las fuerzas puntuales,\(U = U(P_i)\). Mantengamos todas las fuerzas puntuales en valores fijos y variemos solo una, digamos\(P_k\). Para el equilibrio, la energía potencial total del sistema debe ser estacionaria con respecto a este cambio. Por lo tanto,
\[\delta \prod = \delta (U - W) = \frac{dU}{dP_k} \delta P_k − w_k \delta P_k \\ = \left( \frac{dU}{dP_k} − w_k \right) \delta P_k = 0\]
El teorema extendido de Castigliano es
\[w_k = \frac{\partial U(P_i)}{\partial P_k} \]
Por ejemplo, si se aplican dos cargas puntuales,
\[w_2 = \frac{\partial U(P_1, P_2)}{\partial P_2} \]
Por lo general, el teorema de Castigliano da solo deflexión en un punto dado pero no la forma desviada. El teorema extendido puede usarse para predecir la forma desviada.
Ilustración
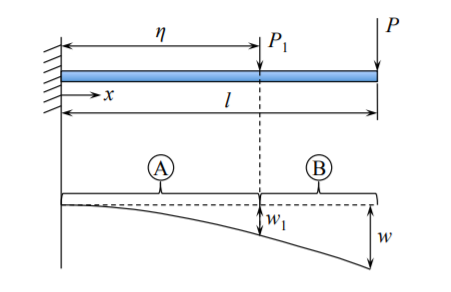
Considera una viga en voladizo cargada por dos fuerzas puntuales. Una fuerza\(P\) se aplica en la punta y la otra fuerza\(P_1\) actúa a cierta\(\eta\) distancia del soporte.
La distribución del momento de flexión es
\[\begin{array}{lcl} M_A(x) = P(l − x) + P_1(\eta − x) & \text{ for } & 0 < x < \eta \\ M_B(x) = P(l − x) & \text{ for } & \eta< x < l \end{array}\]
La energía de deformación por flexión es
\[U(P, P_1) = \frac{1}{2EI} \int_{0}^{\eta} M^2_{A} dx + \frac{1}{2EI} \int_{\eta}^{l} M^2_B dx \]
Según la ecuación\ ref {8.49}, la deflexión bajo la carga puntual\(P_1\) es
\[w_1 = \frac{\partial U(P, P_1)}{\partial P_1} = \frac{1}{EI} \int_{0}^{\eta} M_A \frac{\partial M_A}{\partial P_1} dx + \frac{1}{EI} \int_{\eta}^{l} M_B \frac{\partial M_B}{\partial P_1} dx\]
Los derivados de los momentos de flexión son
\[\frac{\partial M_A}{\partial P_1} = \eta − x \]
\[\frac{\partial M_B}{\partial P_1} = 0 \]
Sustituyendo ecuaciones\ ref {8.51} y (?? ) en (?? ), uno obtiene
\[w_1 = \frac{1}{EI} \int_{0}^{\eta} [P(l − x) + P_1(\eta − x)](\eta − x) dx \]
Esta ecuación es válida para cualquier combinación de\(P\) y\(P_1\). Por lo tanto, podemos suponer que\(P_1\) es una fuerza “ficticia” y se puede establecer igual a cero. Entonces, Ecuación (?? ) reduce a
\[w_1 = \frac{1}{EI} \int_{0}^{\eta} [P(l − x)(\eta − x) dx \]
lo que da, después de la integración,
\[w_1(\eta) = \frac{Pl^3}{3EI} \left[ \frac{3}{2} \left(\frac{\eta}{l}\right)^2 − \frac{1}{2} \left(\frac{\eta}{l}\right)^3 \right] \]
En la solución anterior\(\eta\) se encuentra una posición arbitraria a lo largo de la viga y\(w_1(\eta)\) es la deflexión correspondiente. Cambiando las variables
\[\eta \rightarrow x \\ w_1(\eta) = w(x) \]
podemos recuperar la forma exacta desviada de la viga voladiza
\[w_1(\eta) = \frac{Pl^3}{3EI} \left[ \frac{3}{2} \left(\frac{x}{l}\right)^2 − \frac{1}{2} \left(\frac{x}{l}\right)^3 \right] \]
El ejemplo anterior ilustró una gran flexibilidad del método Castigliano para resolver problemas estáticamente determinados.


