7.5: Solución por expansión Taylor

Última actualización
Guardar como PDF

Page ID: 85095

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Considere el mismo problema de muestra de la viga en voladizo bajo la fuerza del punto de punta. Asumir la solución como una serie de potencia

\[w(x) = \sum^{N}_{n=1} a_n x^n \label{7.5.1}\]

Para ilustración, trunca la serie tomando los cuatro primeros términos

\[w(x) = a_0 + a_1x + a_2x^2 + a_3x^3 \]

Las condiciones de contorno cinemático son

\[w(x = 0) = 0; \quad w^{\prime}(x = 0) = 0 \]

Es fácil ver que se cumplen las condiciones de contorno de desplazamiento si\(a_o = a_1 = 0\). Los desplazamientos, pendientes y curvatura se convierten

\[w(x) = a_2x^2 + a_3x^3 \]

\[w^{\prime}(x) = 2a_2x + 3a_3x^2 \]

\[w^{\prime\prime}(x) = 2a_2 + 6a_3x \]

El desplazamiento de la punta es

\[w(x = l) = w_o = a_2l^2 + a_3l^3 \]

La expresión de la energía potencial total es

\[\prod = \frac{EI}{2} \int_{0}^{l} (2a + 6a_3x)^2 dx − P(a_2l^2 + a_3l^3 ) \]

o después de la integración

\[\prod = \frac{EI}{2} (4a^2_2 l + 12a_2a_3l^2 + 12a^2_3 l^3 ) − P(a_2l^2 + a_3l^3 ) \]

Lo estacionario de\(\prod(a_2, a_3)\) implica que

\[\frac{\partial \prod}{\partial a_2} = 0, \quad \frac{\partial \prod}{\partial a_3} = 0 \]

lo que lleva a dos ecuaciones algebraicas lineales para\(a_2, a_3\)

\[4a_2 + 6a_3l = \frac{Pl}{EI} \]

\[6a_2 + 12a_3l = \frac{Pl}{EI} \]

donde está la solución

\[a_2 = \frac{Pl}{2EI}, a_3 = − \frac{P}{6EI} \]

La deflexión de la viga es entonces

\[w(x) = \frac{P}{EI} \left( \frac{lx^2}{2} − \frac{x^3}{6} \right) \]

Se obtiene la deflexión de la punta

\[w_o = w(x = l) = \frac{Pl^3}{3EI} \]

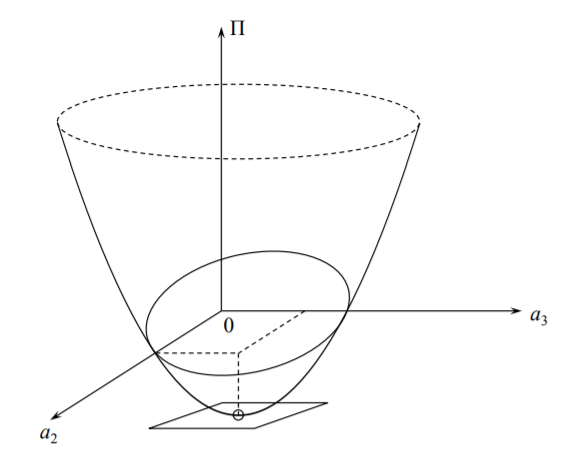
Esta es la solución exacta del problema. La solución exacta se obtuvo en este caso debido a que los primeros cuatro términos de la expansión de Taylor contenían la forma desviada real. Obsérvese que la solución exacta se obtuvo por el método Ritz sin imponer las condiciones de límite estático en la punta\(V = −P\) y\(M = 0\). La interpretación gráfica de la condición estacionaria con dos grados de libertad se obtiene trazando la Ecuación\ ref {7.5.1} en el espacio\((\prod, a_2, a_3)\), Figura (\(\PageIndex{1}\)).

7.5.1.png — Figura\(\PageIndex{1}\): La energía potencial como paraboloide.