8.1: Preludio a la Estabilidad de Estructuras Elásticas
- Page ID
- 85130
En el Capítulo 7 hemos formulado la condición de equilibrio estático de cuerpos y estructuras mediante el estudio de un pequeño cambio (variación) de la energía potencial total. Se dijo que el sistema estaba en equilibrio si la primera variación de la energía potencial total desaparece. El análisis no dijo nada sobre la estabilidad del equilibrio. La presente conferencia dará una respuesta a esa pregunta al examinar con más atención lo que está sucediendo en las proximidades del estado de equilibrio.
Para ilustrar el concepto, considere un cuerpo rígido (una bola) ubicado en un paraboloide axisimétrico. mostrado en la Figura (\(\PageIndex{1}\)).
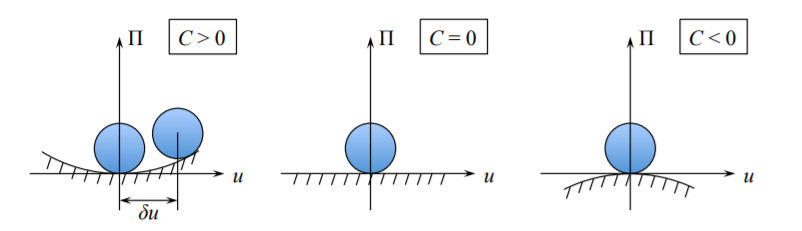
En el caso de un cuerpo rígido la energía potencial total es solo la energía potencial
\[\prod = mgh = Cu^2 \]
donde u es el desplazamiento horizontal de la pelota desde la posición de reposo. Calculemos la primera y segunda variación de la función\(\prod (u)\)
\[\delta \prod = \frac{\partial\prod}{\partial u} \delta u = 2Cu \delta u \]
\[\delta^2 \prod = \delta (\delta \prod) = 2C \delta u \delta u \]
En el origen del sistema de coordenadas\(u = 0\), por lo que la primera variación de\(\prod\) es cero sin importar cuál sea el signo del coeficiente\(C\). En la expresión para la segunda variación, el producto siempre\(\delta u \delta u = (\delta u)^2\) es no negativo. Por lo tanto, el signo de la segunda variación depende del signo del coeficiente\(C\). De la Figura\(\PageIndex{1}\) inferimos que\(C > 0\) corresponde a una configuración estable. El balón desplazado en una pequeña cantidad\(\delta u\) volverá a la posición original. Por el contrario, para\(C < 0\), la pelota, cuando se desplaza en una pequeña cantidad\(\delta u\), rodará hacia abajo y desaparecerá. A esto lo llamamos un comportamiento inestable. El caso\(C = 0\) corresponde al equilibrio neutro.
Se puede formalizar la consideración anterior al cuerpo elástico (estructura), donde la energía potencial total es una función de un parámetro escalar, como una amplitud de desplazamiento\(u\). La función se\(\prod (u)\) puede ampliar en la serie Taylor alrededor del punto de referencia\(u_o\)
\[\prod (u) = \prod (u_o) + \left. \frac{d\prod}{du} \right|_{u=u_o} (u − u_o) + \frac{1}{2} \left. \frac{d^2\prod}{du^2}\right|_{u=u_o} (u − u_o)^2 + \dots \]
El cambio incremental de la energía potencial\(\Delta \prod = \prod (u) − \prod (u_o)\) tras una pequeña variación del argumento\(\delta u = u − u_o\) es
\[\Delta \prod = \frac{d\prod}{du} \delta u + \frac{1}{2} \frac{d^2 u}{du^2} (\delta u)^2 = \delta \prod + \delta^2 \prod + \dots \]
Para el sistema en equilibrio la primera variación debe ser cero. Por lo tanto, a la expansión de segundo término, el signo del incremento de\(\prod\) depende del signo de la segunda variación de la energía potencial. Ahora podemos distinguir tres casos
\[\delta^2 \prod \begin{cases} > 0, & \text{ Positive (stable equilibrium)} \\ = 0, & \text{ Zero (neutral equilibrium)} \\ < 0, & \text{ Negative (unstable equilibrium)} \end{cases} \nonumber \]


