8.2: Condición Trefftz para Estabilidad
- Page ID
- 85142
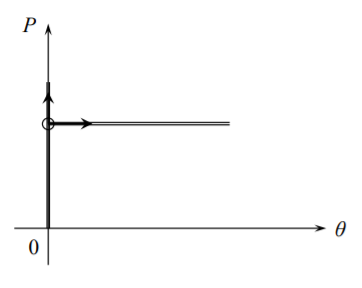
En 1933 el científico alemán Erich Trefftz propuso el criterio energético para la determinación de la estabilidad de las estructuras elásticas. Explicaremos este criterio sobre un ejemplo sencillo de una estructura de un grado de libertad. Considera una columna rígida libre en un extremo y articulada en el otro. Hay un resorte torsional montado en la bisagra. Al girar un ángulo\(\theta\), se desarrolla un momento de flexión en la bisagra, resistiendo el movimiento
\[M = K \theta\]
donde\(K\) es la constante del resorte rotacional. La columna se encuentra inicialmente en posición vertical y es cargada por una carga compresiva\(P\), Figura (\(\PageIndex{1}\)). En la configuración deformada, la fuerza\(P\) ejerce un trabajo sobre el desplazamiento\(u\)
\[u = l(1 − \cos \theta) \cong l \frac{\theta^2}{2} \label{8.2.2}\]
La energía potencial total del sistema es
\[\prod = \frac{1}{2} M \theta − P u = \frac{1}{2} K \theta^2 − \frac{1}{2} Pl \theta^2 \]
Tras la aplicación de carga, la columna es, por supuesto, rígida y permanece recta hasta el punto crítico\(P = P_c\). El camino\(\theta = 0\) se llama el camino de equilibrio primario. Si la columna fuera elástica en lugar de rígida, solo habría compresión axial a lo largo de esa trayectoria. Esta etapa a menudo se conoce como una configuración de prepandeo. En la carga crítica\(P_c\) la estructura tiene dos opciones. Puede seguir resistiendo la fuerza\(P > P_c\) y permanecer recto. O puede bifurcarse a la configuración vecina y continuar girando a una fuerza constante. El punto de bifurcación es el punto de pandeo. Se dice que la estructura se abrocha desde la etapa puramente compresiva hasta la etapa de una compresión y flexión combinadas.
El análisis anterior ha demostrado que considerando el equilibrio con términos geométricos no lineales, la Ecuación\ ref {8.2.2} predice dos trayectorias de equilibrio distintas y un punto de bifurcación (pandeo). Ahora vamos a explorar un poco más la noción de estabilidad y calcular la segunda variación de la energía potencial total
\[\delta^2 \prod = (K − Pl) \delta \theta \delta \theta \]
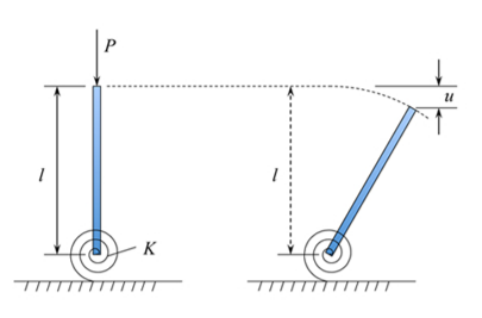
La gráfica de la segunda variación normalizada\(\delta^2 \prod / \delta \theta \delta \theta \) se muestra en la Figura (\(\PageIndex{1}\)).
Se ve que en el rango\(0 < P < P_c\), la segunda variación de la energía potencial total es positiva. En el rango\(P > P_c\), esa función es negativa. Una transición del comportamiento estable al inestable ocurre en\(\delta^2 \prod = 0\). Por lo tanto, la fuga de la segunda variación de la energía potencial total identifica el punto de inestabilidad estructural o pandeo.
Físicamente, la prueba de estabilidad se ve así. Llevamos la fuerza de compresión al valor\(P^*\), aún por debajo de la carga crítica. Luego aplicamos una pequeña rotación\(\pm \delta\theta\) en cualquier dirección del plano de pandeo. El producto\(\delta\theta\delta\theta\) es siempre no negativo.
Para el equilibrio debe desterrar la primera variación de la energía potencial total,\(\delta\theta = 0\), lo que da
\[(K − Pl) \theta \delta \theta = 0 \]
Hay dos soluciones de la ecuación anterior, que corresponde a dos caminos de equilibrio distintos:
- \(\theta = 0 - \text{ primary equilibrium path}\)
- \(P = P_c = \frac{K}{l} - \text{ secondary equilibrium path}\)
Y así es la segunda variación de la energía potencial total (longitud AB en la Figura (\(\PageIndex{1}\))). Cuando se libera la carga lateral necesaria para desplazar la\(\delta\theta\) columna, el sistema de muelles volverá a la posición recta sin deformar.
Repetimos la misma prueba bajo la fuerza compresiva\(p^{**} > P_c\). La aplicación de la rotación infinitesimal\(\delta\theta\) hará que la función sea\(\delta^2/\delta\theta\delta\theta\) negativa. Este es un rango de comportamiento inestable. Al liberar la fuerza transversal, la columna no volverá a la posición vertical, sino que permanecerá en la configuración deformada. Cabe señalar que el análisis anterior se refiere al problema de la estabilidad del camino de equilibrio primario. El camino de equilibrio secundario es estable, como se mostrará a continuación.
Para expresar el potencial total, se puede construir con la ecuación exacta para el desplazamiento\(u\) en lugar de la primera expansión de dos términos, Ecuación\ ref {8.2.2}
\[\prod = \frac{1}{2} K\theta^2 − lP(1 − \cos \theta) \]
El camino de equilibrio secundario obtenido de\(\delta \prod = 0\) es
\[\frac{P}{P_c} = \frac{\theta}{\sin \theta}\]
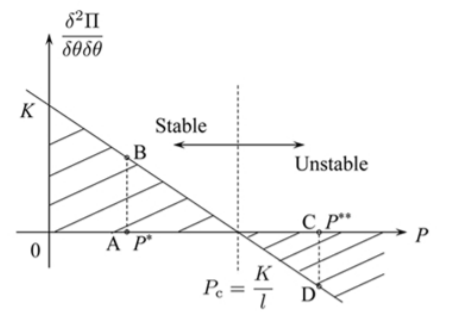
La gráfica de la función anterior se muestra en Figura (\(\PageIndex{4}\)).
Para valores pequeños de la rotación de la columna, la fuerza\(P\) es casi constante, como lo predice la expansión a dos términos de la función coseno. Para rotaciones más grandes, la resistencia de la columna aumenta con el ángulo\(\theta\). Tal comportamiento es inherentemente estable. La fuerza está aumentando monótonamente y alcanza el infinito en\(\theta \rightarrow \pi\).