8.7: Transición de modo (Avanzada)
- Page ID
- 85149
Ecuación de equilibrio de momento
Para una columna soportada por pasador, la forma de la imperfección\(\bar{w}(x)\) y la deformación\(w(x)\) satisfacen la ecuación de equilibrio de momento
\[EIw^{\prime \prime} + P w = EI\bar{w}^{\prime \prime} \label{9.77}\]
Las soluciones deben satisfacer las condiciones de límite
\[\begin{align*} w(0) &= 0 \\[4pt] w^{\prime \prime}(0) &= 0 \\[4pt] w(l) &= 0 \\[4pt] w^{\prime \prime}(l) &= 0 \end{align*}\]
Por supuesto, las soluciones también deben satisfacer las condiciones continuas:\(w(x)\) y\(w^{\prime}(x)\) son continuas a lo largo de toda la longitud de la columna, es decir, no se produce ningún paso o doblez en las soluciones.
Podemos ampliar la imperfección\(\bar{w}(x)\) en series de Fourier como
\[\bar{w}(x) = \sum^{\infty}_{n=1} A_n \sin \frac{n \pi x}{l} \label{9.79}\]
Los coeficientes\(A_n\) pueden ser determinados por la transformación de Fourier de\(\bar{w}\):
\[A_n = \frac{2}{l} \int_{0}^{l} \bar{w}(x) \sin \frac{n \pi x}{l} dx \]
La deformación\(w(x)\) bajo una carga se\(P\) puede escribir como una suma de un conjunto completo de series de Fourier
\[w(x) = \sum^{\infty}_{n=1} B_n \sin \frac{n \pi x}{l} \label{9.81}\]
donde se\(B_n\) puede determinar por la Ecuación\ ref {9.77}.
La ecuación\ ref {9.77} ahora se convierte
\[ -\sum^{\infty}_{n=1} B_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l} + \frac{P}{EI} \sum^{\infty}_{n=1} B_n \sin \frac{n \pi x}{l} = - \sum^{\infty}_{n=1} A_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l}\]
Para que la ecuación se mantenga, los coeficientes deben satisfacer
\[−B_n \frac{n^2 \pi^2} {l^2} + \frac{P}{EI} B_n = −A_n \frac{n^2 \pi^2} {l^2} \]
Resolver para\(B_n\), obtenemos
\[B_n = A_n \frac{1}{1 − \bar{P}/n^2} \]
aquí, definimos\(\bar{P} = P/P_c\) y\(P_c = \frac{\pi^2 EI}{l^2}\). Entonces, la deformación\(w(x)\) es
\[w(x) = \sum^{\infty}_{n=1} A_n \frac{1}{1 − \bar{P}/n^2} \sin \frac{n \pi x}{l} \]
La solución nos dice cuál es la forma de la deformación, pero no nos dice nada sobre la estabilidad de la forma de equilibrio. Si queremos estudiar la estabilidad, tenemos que utilizar el método de energía potencial.
Método de energía potencial
Bajo una carga\(P\), la energía potencial total del sistema de columnas es (debido a la Ecuación (9.2.1) en el Capítulo 9):
\[\prod = \frac{EI}{2} \int_{0}^{l} (w^{\prime \prime} − \bar{w}^{\prime \prime})^2 dx − \frac{P}{2} \int_{0}^{l} (w^{\prime 2} − \bar{w}^{\prime 2}) dx \]
Ecuaciones sustitutas\ ref {9.79} y\ ref {9.81} en ella, tenemos
\[\begin{align*} \prod &= \frac{EI}{2} \int_{0}^{l} (w^{\prime \prime} − \bar{w}^{\prime \prime})^2 dx − \frac{P}{2} \int_{0}^{l} (w^{\prime 2} − \bar{w}^{\prime 2}) dx \\[4pt] &= \frac{EI}{2} \int_{0}^{l} \left[ -\sum^{\infty}_{n=1} B_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l} + \sum^{\infty}_{n=1} A_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l} \right]^2 dx - \frac{P}{2} \int_{0}^{l} \left\{ \left[ \sum^{\infty}_{n=1} B_n \left(\frac{n \pi} {l} \right) \cos \frac{n \pi x}{l} \right]^2 - \left[ \sum^{\infty}_{n=1} A_n \left(\frac{n \pi} {l} \right) \cos \frac{n \pi x}{l} \right]^2 \right\} dx \\[4pt] &= \frac{\pi^4 EI}{4l^3} \sum^{\infty}_{n=1} (B_n - A_n)^2 n^4 - \frac{\pi^2 P}{4l} \sum^{\infty}_{n=1} B_n^2 n^2 + \frac{\pi^2 P}{4l} \sum^{\infty}_{n=1} A_n^2 n^2 \\[4pt] &= \frac{\pi^2 P_c}{4l} \left\{ \sum^{\infty}_{n=1} [(B_n - A_n)^2 n^4 - \bar{P} (b_n^2 - a_n^2) n^2] \right\} \end{align*}\]
La ortogonalidad de las series de Fourier se utiliza para simplificar la integración.
Para obtener la solución de equilibrio, necesitamos la primera derivada de la energía potencial
\[\frac{\partial \prod}{\partial B_n} = 0 \quad \rightarrow \quad B_n = A_n \frac{1}{1 − \bar{P}/n^2} \label{9.88}\]
que es exactamente la misma que la solución dada al resolver la ecuación de equilibrio.
Para ver la estabilidad de la solución, necesitamos la segunda derivada de la energía potencial
\[\frac{\partial^ \prod}{\partial B_n^2} > 0 \quad \rightarrow \quad \bar{P} < n^2 \label{9.89}\]
Podemos ver los siguientes puntos directamente de Ecuaciones\ ref {9.88} y\ ref {9.89}:
- La carga crítica de pandeo para el\(n^{th}\) modo es\(P_c = \frac{n^2\pi^2 EI}{l^2}\).
- Los modos que satisfacen\(n^2 > \bar{P}\) están en equilibrio estable.
- Para los modos que satisfacen\(n^2 < \bar{P}\), todavía podemos resolver por un valor de\(B_n\), pero esos modos son inestables y se adaptarán al infinito más o menos.
Ejemplo\(\PageIndex{1}\)
La imperfección\(\bar{w}(x)\) consiste solo en los dos primeros modos, a saber
\[\bar{w}(x) = A_1 \sin \frac{\pi x}{l} + \sin \frac{2 \pi x}{l} \]
Si\(A_1 = 0\), el punto cero está en el centro de la columna. Si\(A_1 \neq 0\), el punto cero se desplaza una distancia\(u\). \(u\)está dado por
\[u = \frac{\sin^{−1} \frac{A_1}{2}}{\pi} l , \quad 0 \leq A_1 \leq 2 \]
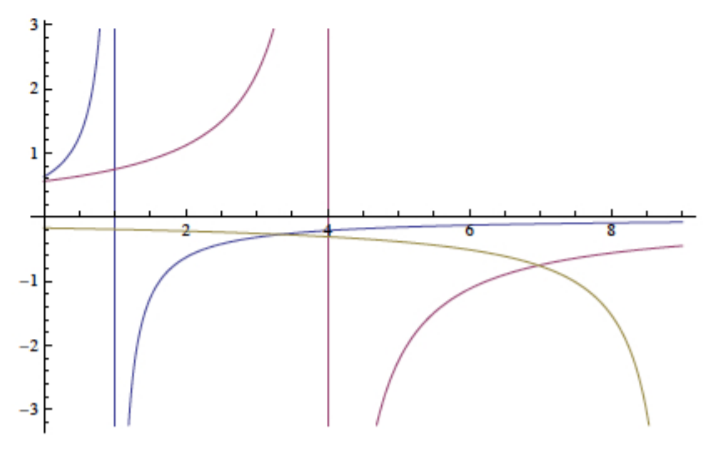
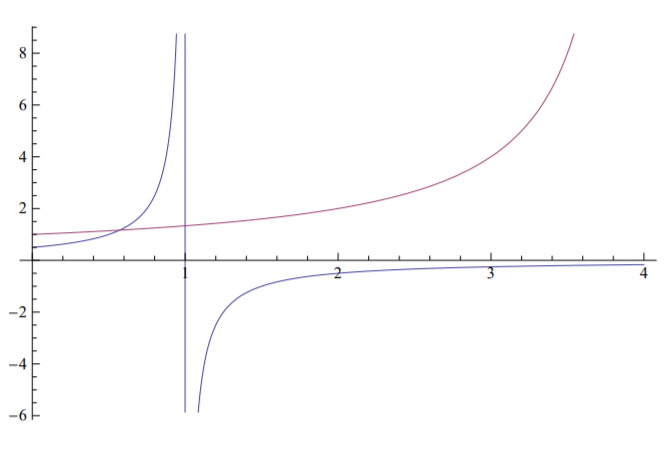
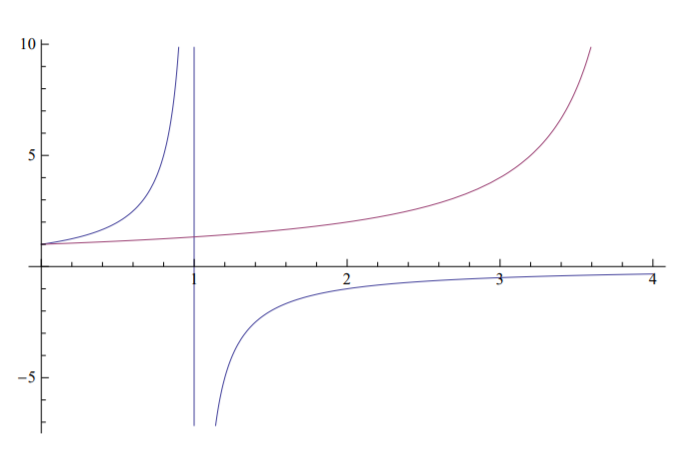
Las amplitudes de deformación frente a las curvas de carga se representan en la Figura (\(\PageIndex{1}\)) para el caso\(A_1 = 0.5\), la Figura (\(\PageIndex{2}\)) para\(A_1 = 1\) y la Figura (\(\PageIndex{3}\)) para\(A_1 = 1.5\).
Ejemplo\(\PageIndex{2}\)
La imperfección está en tal forma que el punto cero se desplaza mientras que ambas secciones son autosimétricas. Tal forma puede describirse como
\[\bar{w}(x) = \begin{cases} \sin \frac{\pi x}{\eta l} & 0 < x < \eta l \\ − \frac{1 − \eta}{\eta} \sin \frac{\pi(x − \eta l)}{(1 − \eta)l} & \eta l < x < l \end{cases} \label{9.92}\]
donde\(0.5 \leq \eta \leq 1\). Cuando\(\eta = 0.7\), se\(\bar{w}(x)\) puede expandir en series de Fourier como:
\[\bar{w}(x) = 0.634 \sin \frac{\pi x}{l} + 0.563 \sin \frac{2 \pi x}{l} − 0.174 \sin \frac{3 \pi x}{l} + 0.071 \sin \frac{4 \pi x}{l} + \dots \]
Como era de esperar, en este caso, dominan los dos primeros modos, pero aún hay modos superiores en la expansión.
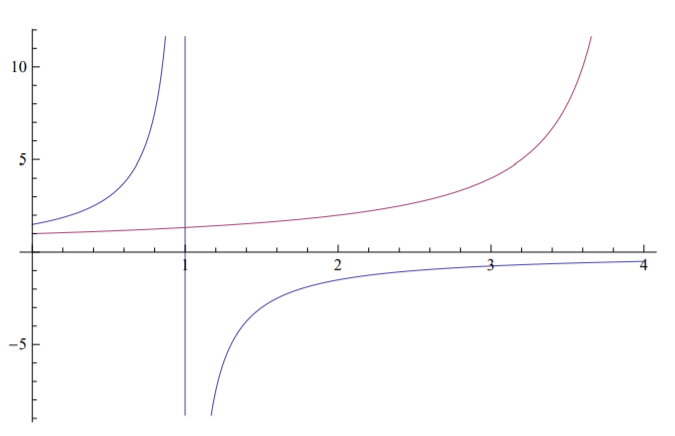
Trazamos las amplitudes de modo vs. carga en la Figura (\(\PageIndex{4}\)). Si la carga\(\bar{P} > 4\), por ejemplo,\(\bar{P} = 7.5\), la amplitud del modo III llega a ser mayor. Entonces, la forma de deformación resuelta se parece más al modo III, aunque la imperfección inicial parece no tener nada que ver con el modo III. Sin embargo, esta forma es muy inestable\(\bar{P} > 2^2\), ya que tanto el modo I como el modo II están en equilibrio inestable. Bajo tal carga, el modo I y el modo II se amplificarán exponencialmente.