9.1: La Columna Más Alta

En 1757 el matemático suizo Leonard Euler presentó la famosa solución para el pandeo de una columna de alfiler bajo carga compresiva en su extremo. También formuló y resolvió el problema mucho más difícil de una columna sin almejas cargada por su propio peso. La pregunta práctica era qué tan alta podría ser la columna prismática antes de que se abroche bajo su propio peso. Para formular este problema, se debe volver a visitar la ecuación de equilibrio de una viga/columna en la dirección axial. En cambio la ecuación\(N^{\prime} = 0\) o\(N = \) const, debemos asumir que hay una fuerza corporal\(q\) por unidad de longitud\(q = A\rho\), donde\(A\) está el área transversal de la columna y\(\rho\) es su densidad de masa. Entonces, el equilibrio en la dirección axial requiere que

\[N^{\prime} = q \quad \text{ or } \quad N = qx + C \]

En el sistema de coordenadas mostrado en la Figura (\(\PageIndex{1}\)), la fuerza axial debe ser cero en\(x = l\).

Figura\(\PageIndex{1}\): Columna cargada en su punta (izquierda) y cargada por su propio peso (derecha).

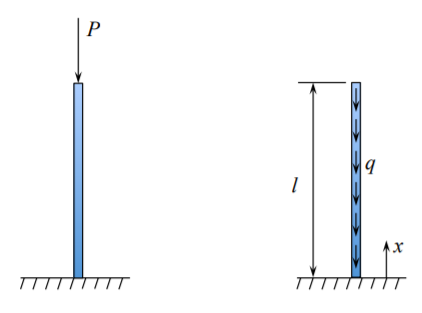
La distribución de la fuerza axial a lo largo de la longitud de la columna es

\[N(x) = −q(l − x) \]

donde el signo menos indica que\(N\) es la fuerza compresiva. Como antes, los parámetros de entrada del problema son\(E\),\(I\)\(q\) y lo desconocido es la longitud crítica\(l_c\).

La derivación del problema de pandeo para una columna clásica presentada en el Capítulo 8 sigue siendo válida pero la fuerza axial en la Ecuación (8.3.11) ya no es constante y por lo tanto debe mantenerse dentro de la integral.

Para el presente problema la primera variación de la energía potencial total es

\[\delta \prod = − \int_{0}^{l} M \delta w^{\prime\prime} dx + \int_{0}^{l} q(l − x)w^{\prime} \delta w^{\prime} dx \label{10.3}\]

Integrando el lado derecho de la ecuación\ ref {10.3} por parte, se obtiene

\[\int_{0}^{l} M^{\prime\prime} + q(l − x)w^{\prime} \delta w dx + \text{ Boundary terms } = 0 \]

donde

\[\text{ Boundary terms } = −\left. M \delta w^{\prime} \right|^{l}_{0} + \left. M^{\prime} \delta w \right|^{l}_{0} + q(l − x) w^{\prime} \delta w \]

en\(x = 0\),\(\delta w = \delta w^{\prime} = 0\); y en\(x = l\),\(M = 0\),\(V = M^{\prime} = 0\) y\(l − x = 0\). Por lo tanto, los términos límite desaparecen (ver la dedicación en la Sección 2.5). Usando la ley de elasticidad,\(M = −EIw^{\prime\prime}\), la ecuación de equilibrio local para el autopandeo de la columna se convierte

\[EI \frac{d^4w}{dx^4} + \frac{d}{dx} \left[ q(l − x) \frac{dw}{dx} \right] = 0 \]

Integrando una vez, obtenemos

\[EI \frac{d^3w}{dx^3} + q(l − x)dw = 0 \label{10.7}\]

La constante de integración es cero debido a que la fuerza de corte desaparece en el extremo libre\(x = l\). La ecuación gobernante es la ecuación diferencial lineal de tercer orden con un coeficiente variable. La solución ya no está representada por la función armónica. La forma de resolver el problema es introducir dos nuevas variables

\[\xi = \frac{2}{3} \sqrt{ \frac{q(l − x)^3}{EI}}, \quad u = \frac{dw}{d\xi} \]

Luego, la ecuación\ ref {10.7} se transforma en la ecuación de Bessel

\[\frac{d^2 u}{d\xi^2} + \frac{1}{\xi} \frac{du}{d\xi} + (1 − \frac{1}{9\xi^2} )u = 0 \]

Omitiendo los detalles del cálculo, se encuentra que la longitud crítica de la columna es

\[l^3_c = \frac{9EI}{4q} j^2_{\frac{1}{3}} \]

donde\(j_{\frac{1}{3}} = 1.866\) está la raíz de la función Bessel del tercer tipo. Por último

\[l^3_c = 7.837 \frac{EI}{q} \]

El peso total del material de la columna es\(N_c = l_cq\). En cuanto al peso total, la longitud crítica es

\[l^2_c = 7.84 \frac{EI}{N_c} \label{10.12}\]

A modo de comparación, la longitud de la columna de sujeción libre al pandeo cargada por el mismo peso es

\[l^2_c = \frac{\pi^2}{4} \frac{EI}{N_c} = 2.47 \frac{EI}{N_c} \]

La parte inferior de ambas columnas ve el mismo peso, pero la longitud crítica de la columna sometida a autopandeo es\(\sqrt{\frac{7.84}{2.47}} = 1.78\) veces más alta que una columna de sección transversal similar cargada en su punta.

Ejemplo\(\PageIndex{1}\)

Un mástil tubular de acero incorporado sólidamente en la base y está libre en su parte superior. El cilindro es\(t = 3\) mm de espesor y tiene un radio de\(R = 50\) mm. ¿Cuál es la longitud crítica del mástil para abrocharse bajo su propio peso?

El peso total del mástil es

\[N_c = Al \rho\]

donde\(A\) está el área de la sección transversal,\(A = 2\pi Rt\). El segundo momento de inercia del tubo de pared delgada es\(I = \pi R^3 t\). De la ecuación\ ref {10.12}

\[l^2_c = 7.84 \frac{E \pi R^3 t}{2 \pi Rtl_c \rho} \]

de la cual se obtiene

\[l_c = \sqrt[3]{\frac{3.92ER^2}{\rho}} = 65 m \]

La solución anterior se aplica a una columna prismática de sección transversal constante.

La solución aproximada se puede derivar de la condición Trefftz\(\delta^2 \prod = 0\). Partiendo de la ecuación\ ref {10.3} y realizando la segunda variación se obtiene

\[EI \int_{0}^{l} \delta w^{\prime\prime} \delta w^{\prime} dx + \int_{0}^{l} q(l − x)\delta w^{\prime} \delta w dx \]

La fuerza crítica del cuerpo compresivo es entonces

\[q = EI \frac{\int_{0}^{l} \phi^{\prime\prime} \phi^{\prime\prime} dx}{\int_{0}^{l} (l − x)\phi^{\prime}\phi^{\prime} dx} \label{10.18}\]

En comparación con la fórmula estándar de Trefftz para columna cargada con punta, existe el término\((l − x)\) en el denominador. Como ejemplo, considere la forma de deflexión parabólica más simple

\[\phi = x^2 \]

\[\phi^{\prime} = 2x \]

\[\phi^{\prime\prime} = 2 \]

Introduciendo la expresión anterior en la Ecuación\ ref {10.18}, el peso crítico de pandeo por unidad de longitud es

\[q = \frac{12EI}{l^3} \]

El error en esta aproximación es\(\frac{12 − 7.837}{7.837} = 53\%\) que no es bueno. Como segundo ensayo, considere una función de forma de potencia con un exponente fraccionario\(\alpha\)

\[\phi = x^{\alpha} \]

\[\phi^{\prime} = \alpha x^{\alpha−1} \]

\[\phi^{\prime\prime} = \alpha(\alpha − 1)x^{\alpha−2} \]

La solución resultante es

\[q = \frac{2EI}{l^3} \frac{\alpha(\alpha − 1)(2\alpha − 1)}{2\alpha − 3} \]

El parámetro crítico de pandeo alcanza un mínimo en\(\alpha = 1.75\). La carga mínima de pandeo es

\[q_{\text{min}} = 9.8 \frac{EI}{l^3} \]

El error se corta a la mitad pero sigue siendo grande al 25%. En el tercer intento, consideremos la función trigonométrica

\[\phi = 1 − \cos \frac{\pi x}{2l} \label{10.24a}\]

\[\phi^{\prime} = \left(\frac{\pi}{2l}\right) \sin \frac{\pi x}{2l} \]

\[\phi^{\prime\prime} = \left( \frac{\pi}{2l} \right)^2 \cos \frac{\pi x}{2l} \label{10.24c}\]

Además de satisfacer la condición cinemática sujeta en\(x = 0\), la forma del coseno da el momento de flexión cero en la parte superior. Sustituyendo Ecuaciones\ ref {10.24a} -\ ref {10.24c} en la condición Trefftz, Ecuación (10.18), se obtiene la siguiente solución de forma cerrada

\[q = \frac{EI}{l^3} \frac{\pi^4}{2(\pi^2 − 4)} = 8.29 \frac{EI}{l^3} \]

que difiere en solo 6% de la solución exacta. La verdadera forma de la columna que se abrocha por su propio peso es la función Bessel pero la función trigonométrica proporciona una muy buena aproximación.

Por más de 200 años la solución de Euler de pandeo de una columna bajo su propio peso permanece incuestionable. En 1960 Keller y Niordson se preguntaron por cuánto se puede aumentar la altura de la columna. Si el mismo volumen de material se distribuye como una estructura prismática de sección transversal constante del radio\(r = 0.1\) m, la longitud de la columna sería

\[l = \frac{V}{\pi r^2} = \frac{1}{\pi 0.1^2} = 32 m \nonumber \]

y el peso por unidad de longitud de una columna fija será

\[q = \frac{V}{l} = \frac{7.8 \times 10^4}{32} = 24 N/m \nonumber \]

Usando la ecuación\ ref {10.12} podemos verificar si dicha columna permanecerá o se doblará bajo su propio peso

\[l^2_c = 7.84 \frac{EI}{N} \nonumber \]

dónde\(I = \frac{\pi r^4}{4}\),\(N = V \rho\) y\(E = 2.1 \times 10^{11} N/m^2\). Sustituyendo los valores anteriores, la longitud crítica se convierte en\(l_c = 26\) m. Esto significa que la columna prismática de 32 m se doblará y no se podrá erigir. Al dar forma a la columna de acuerdo con la Figura (\(\PageIndex{2}\)) su longitud se puede aumentar por un factor de\(86/26 = 3.3\).

Si la sección transversal es variable, esta pregunta ha llevado a un problema matemático muy complejo. Algunos aspectos de esta solución todavía están estudiados hasta ahora. El problema está bien planteado si se busca la solución óptima bajo un volumen constante, dado del material. No existe una solución simple de forma cerrada al problema por lo que la respuesta se obtiene a través de la optimización numérica, ver Figura (\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): La forma de la columna más alta.

Tenga en cuenta que la altura de la columna se redujo para que quepa en la página. Para que te hagas una idea, la columna de acero del volumen total de 1.0 m\(^3\) y el radio desnudo de 10 cm podrían ser tan altos como\(l = 86 \) m.