9.2: Comportamiento de deflexión para viga con cargas axiales de compresión y cargas transversales

Figura\(\PageIndex{1}\): Viga simplemente soportada con carga transversal intermedia.

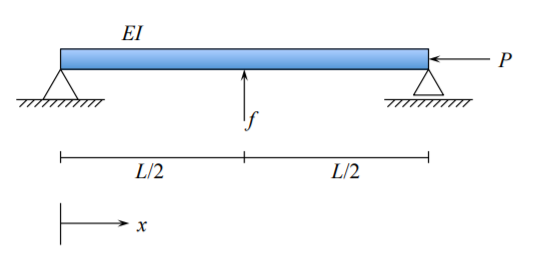
Considere una viga simplemente soportada con una carga fija\(f\) aplicada en el centro como se muestra en la Figura (\(\PageIndex{1}\)). Adicionalmente, la viga está sometida a una carga axial compresiva\(P\). La energía potencial total para este sistema mecánico es

\[\left. \prod \right._{\text{total}} = \int_{0}^{L} \frac{1}{2} EI(v^{\prime\prime})^2 dx − \int_{0}^{L} \frac{1}{2} (v^{\prime})^2 dx − fv \left(\frac{L}{2}\right) \]

Si\(f = 0\), estamos ante un problema clásico de pandeo; es decir, la viga permanece recta hasta que se alcanza una carga crítica después de lo cual la viga se dobla repentinamente. La carga crítica para la configuración mostrada es\(P_{cr} = \pi^2 EI/L^2\). Investiguemos el comportamiento para\(f \neq 0\).

Los puntos estacionarios de la energía potencial aún dan las soluciones\(v(x)\) que satisfacen el equilibrio. Calculemos una solución aproximada usando el formulario

\[ v(x) \approx C \sin \left(\pi \frac{x}{L}\right) \]

Las derivadas de esta función son

\[ v^{\prime}(x) = C \frac{\pi}{L} \cos \left(\pi \frac{x}{L}\right) \nonumber \]

\[v^{\prime\prime}(x) = - C \left(\frac{\pi}{L}\right)^2 \sin \left(\pi \frac{x}{L}\right) \nonumber\]

Inserción de estos en los rendimientos potenciales de energía

\[\left. \prod \right._{\text{total}} = \int_{0}^{L} \frac{1}{2} EI \left(\frac{\pi}{L}\right)^4 C^2 \sin^2 \left(\pi \frac{x}{L}\right) dx \\ − P \int_{0}^{L} \frac{1}{2} \left(\frac{\pi}{L}\right)^2 C^2 \cos^2 \left(\pi \frac{x}{L}\right) dx - fC \sin \left(\pi \frac{L/2}{L}\right) \\ = \int_{0}^{L} \frac{1}{2} EI \left(\frac{\pi}{L}\right)^4 C^2 \left[ \frac{1}{2} - \frac{1}{2} \cos \left(\frac{2 \pi x}{L}\right) \right] dx \\ − P \int_{0}^{L} \frac{1}{2} \left(\frac{\pi}{L}\right)^2 C^2 \left[ \frac{1}{2} + \frac{1}{2} \cos \left(\frac{2 \pi x}{L}\right) \right] dx - fC \\ = \frac{1}{4} EI \left(\frac{\pi}{L}\right)^4 C^2L − P \frac{1}{4} \left(\frac{\pi}{L}\right)^2 C^2L - fC \nonumber\]

La condición estacionaria rinde

\[0 = \frac{d \prod_{\text{total}}}{dC} = \frac{1}{2} EI \left(\frac{\pi}{L}\right)^4 CL − P \frac{1}{2} \left(\frac{\pi}{L}\right)^2 CL - f = C \left[ \frac{1}{2} EI \left(\frac{\pi}{L}\right)^4 L − P \frac{1}{2} \left(\frac{\pi}{L}\right)^2 L \right] − f = 0 \]

y por lo tanto

\[C = \frac{f}{\frac{EI \pi^4}{2L^3} − P\frac{\pi^2}{2L}} \\ = \frac{f2L/\pi^2}{\frac{EI\pi^2}{L^2} − P} \\ = \frac{2L}{\pi^2}\frac{f}{P_{cr} − P}\]

La solución aproximada tiene la forma

\[v(x) \approx \frac{2L}{\pi^2}\frac{f}{P_{cr} − P} \sin \left( \pi \frac{x}{L}\right)\]

La deflexión central\(w_o = v(x = \frac{l}{2}) \) es

\[w_o = \frac{fl^3}{48.7EI}\frac{1}{1 − \frac{P}{P_c}} \label{10.31}\]

Para carga axial cero, la ecuación\ ref {10.31} predice una relación lineal entre la carga de punto lateral y la deflexión\(w_o\). El coeficiente aproximado\(\frac{\pi^4}{2} \cong 48.7\) es muy cercano al valor exacto 48 para la columna pin-pin cargada por la fuerza puntual\(f\). La relación lineal se mantiene también para cualquier valor constante de\(P/P_c\). Se obtiene una imagen mucho más interesante fijando la carga lateral y cambiando la carga axial. La ecuación\ ref {10.31} se puede escribir como

\[w_o = \frac{\eta}{1 − \frac{P}{P_c}}, \text{ where } \eta = \frac{fl^3}{48.7EI} \]

que se representa en la Figura (9.3.1). Tenga en cuenta que la fuerza positiva está en compresión mientras que la negativa en tensión. La aplicación de la fuerza lateral desvía la viga por la cantidad\(\eta\). Entonces, al aplicar la carga compresiva en el plano, la viga-columna se comporta como una columna imperfecta. Al invertir el signo de la carga en el plano de compresión a tensión, la deflexión central se vuelve más pequeña y desaparece con\(P/P_c \rightarrow \infty\). Esto es totalmente consistente con nuestra experiencia diaria de que al apretar la cuerda/cable, su deflexión se reduce.