11.4: Condición de Rendimiento
- Page ID
- 85195
De la sección anterior, la condición de rendimiento uniaxial bajo tensión/compresión en la dirección x es
\[\sigma_{11} = \pm \sigma_y \]
En el 3-D general, los seis componentes del tensor de tensión contribuyen al rendimiento del material. La condición de rendimiento de von Mises toma la forma
\[\frac{1}{2} [(\sigma_{11} − \sigma_{22})^2 + (\sigma_{22} − \sigma_{33})^2 + (\sigma_{33} − \sigma_{11})^2 ] + 3(\sigma^2_{12} + \sigma^2_{23} + \sigma^2_{31})] = \sigma^2_y \]
o en una notación de mano corta
\[F(\sigma_{ij}) = \sigma_y \nonumber \]
La derivación paso a paso de la ecuación anterior se da en la siguiente sección. Aquí se consideran varios casos especiales.
Sistema de coordenadas de principio
Todos los componentes no diagonales del tensor de tensión desaparecen,\(\sigma_{12} = \sigma_{23} = \sigma_{31} = 0\). Entonces, la Ecuación (11.3.8) reduce a
\[ (\sigma_1 − \sigma_2)^2 + (\sigma_2 − \sigma_3)^2 + (\sigma_3 − \sigma_1)^2 = 2\sigma^2_y \]
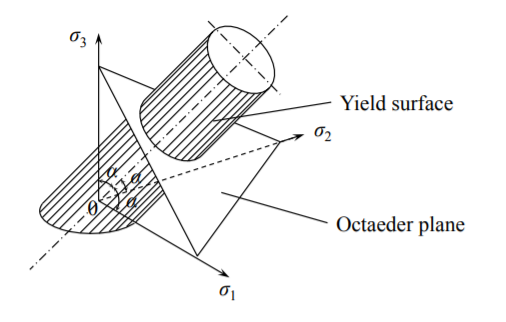
donde\(\sigma_{1}\),\(\sigma_{2}\)\(\sigma_{3}\) son tensiones principales. La representación gráfica de la Ecuación (?? ) es el cilindro de extremo abierto normal al plano octaédrico, Figura (\(\PageIndex{1}\)).
La ecuación de la línea recta normal al plano octaédrico y que pasa por el origen es
\[\sigma_1 + \sigma_2 + \sigma_3 = 3p \]
donde\(p\) esta la presión hidrostatica. Dado que la presión hidrostática no tiene ningún efecto sobre el rendimiento, la superficie elástica es un cilindro abierto.
Estrés plano
Sustituyendo\(\sigma_{13} = \sigma_{23} = \sigma_{33} = 0\) en la Ecuación (11.3.8), la condición de rendimiento por esfuerzo plano se convierte
\[\sigma^2_{11} − \sigma_{11} \sigma_{22} + \sigma^2_{22} + 3\sigma^2_{12} = \sigma^2_y \]
En particular, en cizallamiento puro\(\sigma_{11} = \sigma_{22} = 0\) y\(\sigma_{12} = \sigma_y/\sqrt{3}\). En la literatura\(\sigma_y/\sqrt{3} = k\) se denomina límite elástico en cizallamiento correspondiente a la condición de fluencia de von Mises. En el sistema de coordenadas principal\(\sigma_{12} = 0\) y la condición de rendimiento toma una forma simple
\[\sigma^2_1 − \sigma_1\sigma_2 + \sigma^2_2 = \sigma^2_y \]
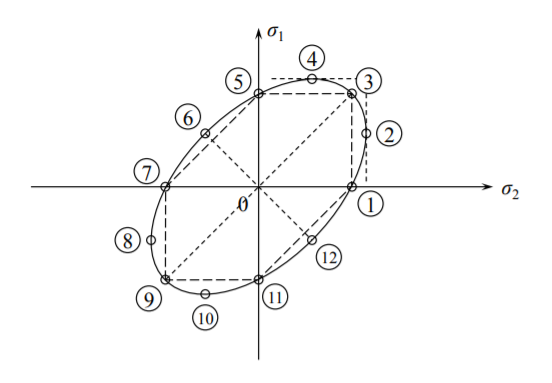
La representación gráfica de la Ecuación (?? ) es la elipse mostrada en la Figura (\(\PageIndex{2}\)). En la Figura (\(\PageIndex{2}\)) se pueden identificar varios estados de estrés importantes.
- Punto 1 y 2: Tensión uniaxial,\(\sigma_{1} = \sigma_{2} = \sigma_{y}\)
- Punto 7 y 11: Compresión uniaxial,\(\sigma_{1} = \sigma_{2} = -\sigma_{y}\)
- Punto 3: Tensión equi-biaxial,\(\sigma_{1} = \sigma_{2}\)
- Punto 9: Compresión equi-biaxial,\(-\sigma_{1} = -\sigma_{2} \)
- Puntos 2, 4, 8 y 10: Tensión simple,\(\sigma_{1} = \frac{2}{\sqrt{3}}\sigma_{y}\)
- Puntos 6 y 12: Cizalla pura,\(\sigma_{1} = -\sigma_{2}\)
El concepto de la deformación plana se explicará en la sección que trata de la regla de flujo.
Tensión equivalente y tasa de deformación equivalente
En el análisis de elementos finitos se utiliza el concepto de la tensión equivalente\(\bar{\sigma}\) o la tensión de von Mises. Se define por en términos de tensiones principales
\[\bar{\sigma} = \frac{1}{2} [(\sigma_{11} − \sigma_{22})^2 + (\sigma_{22} − \sigma_{33})^2 + (\sigma_{33} − \sigma_{11})^2 ] \]
El esfuerzo equivalente\(\bar{\sigma} (\sigma_{ij})\) es la raíz cuadrada del lado izquierdo de la Ecuación (11.3.8). Una vez definida la tensión equivalente, la tasa de deformación equivalente del conjugado de energía se puede evaluar a partir de
\[\bar{\sigma} \bar{\dot{\epsilon}} = \sigma_{ij} \dot{\epsilon_{ij}} \]
y es dada por
\[ \bar{\dot{\epsilon}} = \left\{ \frac{2}{9} [(\dot{\epsilon}_{11} − \dot{\epsilon}_{22})^2 + (\dot{\epsilon}_{22} − \dot{\epsilon}_{33})^2 + (\dot{\epsilon}_{33} − \dot{\epsilon}_{11})^2 ] \right\}^{1/2} \]
La cepa equivalente se obtiene integrando en el tiempo la tasa de deformación equivalente
\[\bar{\epsilon} = \int \bar{\dot{\epsilon}} dt \]


