11.5: Endurecimiento Isotrópico y Cinemático

Última actualización
Guardar como PDF

Page ID: 85180

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Cabe señalar que en el caso de la tensión uniaxial,\(\sigma_2 = \sigma_3 = 0\) y la Ecuación (11.3.10) reduce a\(\bar{\sigma} = \sigma_1\). Asimismo, para la tensión uniaxial\(\dot{\epsilon}_2 = −0.5\epsilon_1\) y\(\dot{\epsilon}_3 = −0.5\epsilon_1\) y la tasa de deformación equivalente se vuelve igual a\(\bar{\dot{\epsilon}} = \dot{\epsilon}_1\). Entonces, según la Ecuación (?? ),\(\bar{\epsilon}_1 = \epsilon_1\). La hipótesis del endurecimiento isotrópico es que el tamaño de la condición de rendimiento instantáneo, representada por el radio del cilindro (Figura (11.4.1)) es una función de la intensidad de la deformación plástica definida por la deformación plástica equivalente\(\bar{\epsilon}\). Así

\[\bar{\sigma} = \sigma_y(\bar{\epsilon}) \]

La función de endurecimiento\(\sigma_y(\bar{\epsilon})\) se determina a partir de una sola prueba, como una tensión uniaxial. En este caso

\[\bar{\sigma} = \sigma_1 = \sigma_y(\bar{\epsilon}) = \sigma_y(\epsilon_1) \]

Así, la forma de la función\(\sigma_y(\bar{\epsilon})\) es idéntica a la curva de endurecimiento obtenida del experimento de tracción. Si la prueba de tracción se ajusta según la ley de endurecimiento por potencia, la tensión equivalente es una función de potencia de la deformación equivalente

\[\bar{\sigma} = A\bar{\epsilon}^n \]

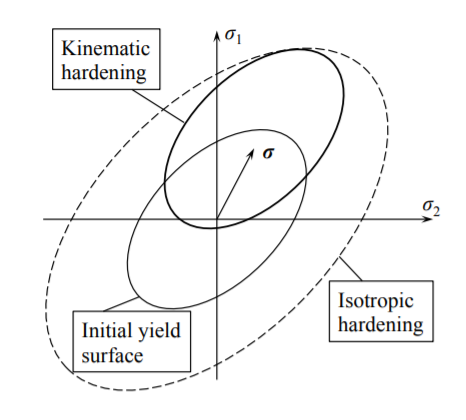
11.5.1.png — Figura\(\PageIndex{1}\): Comparación del endurecimiento isotrópico y cinemático bajo tensión plana.

La función anterior a menudo sirve como entrada a muchos códigos de elementos finitos de propósito general. Una representación gráfica de la regla de endurecimiento 3-D es un crecimiento uniforme de la elipse de rendimiento inicial con deformación equivalente\(\bar{\epsilon}\), Figura (\(\PageIndex{1}\)).

En el caso del endurecimiento cinemático el tamaño de la superficie de rendimiento inicial sigue siendo el mismo, pero el centro de la elipse se desplaza, ver Figura (\(\PageIndex{1}\)). Las coordenadas del centro de la elipse se llama tensión de espalda. El concepto de endurecimiento cinemático es importante para la carga inversa y cíclica. No se seguirá persiguiendo en las presentes notas de conferencia.