11.8: Condición de Rendimiento Tresca

Última actualización
Guardar como PDF

Page ID: 85210

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El estado de tensión en tensión uniaxial de una barra depende de la orientación del plano en el que se resuelven las tensiones. En el Capítulo 2 se demostró que el esfuerzo cortante\(\tau\) en el plano inclinado al plano horizontal por el ángulo\(\alpha\) es

\[\tau = \frac{1}{2} \sigma_{11} \sin 2\alpha \]

donde\(\sigma_{11}\) está el esfuerzo de tracción uniaxial, ver Figura (\(\PageIndex{1}\)).

11.8.1.png — Figura\(\PageIndex{1}\): Esfuerzos cortantes y normales en un corte arbitrario.

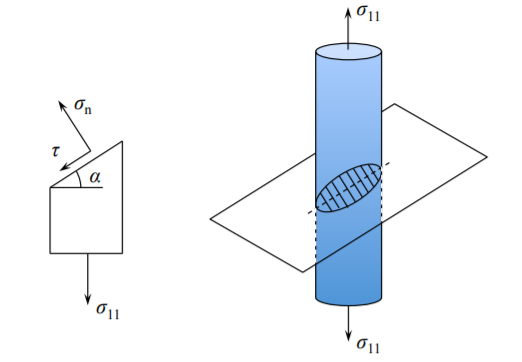
El cizallamiento máximo ocurre cuando\(\sin 2\alpha = 1\) o\(\alpha = \frac{\pi}{4}\). Así, en tensión uniaxial

\[\tau_{\text{max}} = \frac{\sigma_{11}}{2} \]

Extendiendo el análisis al caso 3-D (ver por ejemplo Fung), las tensiones máximas de cizallamiento en tres planos de cizallamiento son

\[\tau_1 = \frac{|\sigma_1 − \sigma_2|}{2}, \quad \tau_2 = \frac{|\sigma_2 − \sigma_1|}{2}, \quad \tau_3 = \frac{|\sigma_3 − \sigma_1|}{2} \]

donde\(\sigma_1\),\(\sigma_2\),\(\sigma_3\) son tensiones principales. En 1860 el científico e ingeniero francés Henri Tresca planteó la hipótesis de que el rendimiento del material se produce cuando el esfuerzo cortante máximo alcanza un valor crítico

\[\tau_o = \text{ max } \left\{ \frac{|\sigma_1 − \sigma_2|}{2}, \frac{|\sigma_2 − \sigma_3|}{2}, \frac{|\sigma_3 − \sigma_1|}{2} \right\} \]

La constante desconocida se puede calibrar a partir de la prueba uniaxial para la que se mantiene la Ecuación (11.4.9). Por lo tanto, al rendimiento\(\tau_o = \sigma_y/2\) y la condición de rendimiento de Tresca toma la forma

\[\text{ max } \{|\sigma_1 − \sigma_2|, |\sigma_2 − \sigma_3|, |\sigma_3 − \sigma_1|\} = \sigma_y \]

En el espacio de tensiones principales la condición de rendimiento de Tresca está representada por un tubo prismático abierto, cuya intersección con el plano octaédrico es un hexágono regular, ver Figura (\(\PageIndex{2}\)).

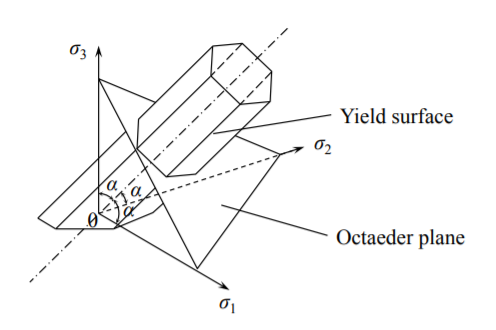
11.8.2.png — Figura\(\PageIndex{2}\): Representación de la condición de rendimiento de Tresca en el espacio de tensiones principales.

Para la tensión plana, la intersección del tubo prismático con el plano\(\sigma_3 = 0\) forma un hexágono familiar de Tresca, mostrado en la Figura (\(\PageIndex{3}\)).

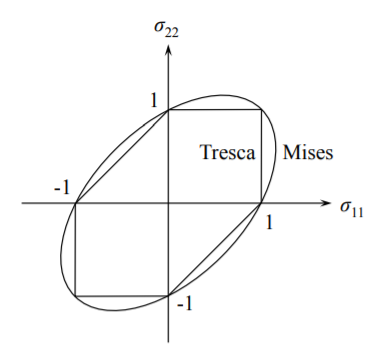
11.8.3.png — Figura\(\PageIndex{3}\): Hexágono de Tresca inscrito en la elipse de von Mises.

El efecto de la presión hidrostática sobre el rendimiento se puede evaluar fácilmente considerando\(\sigma_1 = \sigma_2 = \sigma_3 = p\). Entonces

\[\sigma_1 − \sigma_2 = 0 \]

\[\sigma_2 − \sigma_3 = 0 \]

\[\sigma_3 − \sigma_1 = 0 \]

Bajo este estado de tensión tanto von Mises criterio de rendimiento (Ecuación (?? )) y el criterio de Tresca (Ecuación (?? )) predicen que no habrá rédito.