1.1: Introducción a la Respuesta Elástica

Introducción

Este módulo describe la mecánica básica de la respuesta elástica, un fenómeno físico que los materiales a menudo (pero no siempre) exhiben. Un material elástico es aquel que se deforma inmediatamente después de la carga, mantiene una deformación constante siempre que la carga se mantenga constante, y vuelve inmediatamente a su forma original no deformada cuando se retira la carga. Este módulo también introducirá dos conceptos esenciales en Mecánica de Materiales: estrés y deformación.

Resistencia a la tracción y tensión de tracción

Quizás la prueba más natural de las propiedades mecánicas de un material es la prueba de tensión, en la que una tira o cilindro del material, que tiene longitud L y área transversal A, se ancla en un extremo y se somete a una carga axial P —una carga que actúa a lo largo del eje largo del espécimen- en el otro. (Ver Figura 1). A medida que la carga se incrementa gradualmente, la deflexión axial δ del extremo cargado aumentará también. Finalmente, la muestra de prueba se rompe o hace otra cosa catastrófica, a menudo fracturándose repentinamente en dos o más pedazos. (Los materiales pueden fallar mecánicamente de muchas maneras diferentes; por ejemplo, recuerde cómo se rompen la tiza de pizarra, un trozo de madera fresca y Silly Putty). Como ingenieros, naturalmente queremos entender asuntos tales como cómo δ se relaciona con P, y qué carga de fractura final podríamos esperar en una muestra de diferente tamaño que la original. Como tecnólogos de materiales, queremos entender cómo estas relaciones son influenciadas por la constitución y microestructura del material.

Figura 1: La prueba de tensión.

Uno de los desarrollos históricos fundamentales en nuestra comprensión de las propiedades mecánicas del material fue la constatación de que la resistencia de un espécimen cargado uniaxialmente está relacionada con la magnitud de su área transversal. Esta noción es razonable cuando se considera la fuerza que surge del número de enlaces químicos que conectan una sección transversal con la adyacente a ella como se representa en la Figura 2, donde cada enlace se visualiza como un resorte con cierta rigidez y resistencia. Obviamente, el número de tales enlaces aumentará proporcionalmente con el área de la sección (La densidad superficial de los enlaces NS se puede calcular a partir de la densidad del material\(\rho\), el peso atómico\(W_a\) y el número de Avogadro\(N_A\) como\(N_s = (\rho N_A/W_a)^{2/3}\). Ilustrando para el caso del hierro (Fe):

\[N_S = \left(\dfrac{7.86 \tfrac{\text{g}}{\text{cm}^3} \cdot 6.023 \times 10^{23} \tfrac{\text{atoms}}{\text{mol}}}{55.85 \tfrac{\text{g}}{\text{mol}}}\right)^{\tfrac{2}{3}} = 1.9 \times 10^{15} \dfrac{\text{atoms}}{\text{cm}^2}\nonumber\]

\(N_S \approx 10^{15} \dfrac{\text{atom}}{\text{cm}^2}\)es cierto para muchos materiales.). Por lo tanto, la fuerza axial de un trozo de tiza de pizarra aumentará a medida que el cuadrado de su diámetro. Por el contrario, aumentar la longitud de la tiza no la hará más fuerte (de hecho, probablemente se debilitará, ya que el espécimen más largo será estadísticamente más probable que contenga una falla reductora de la fuerza).

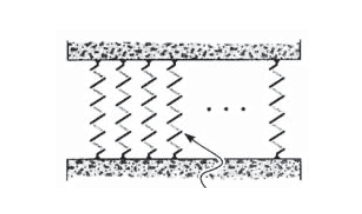
Figura 2: Enlaces interplanares (densidad superficial aproximadamente\(10^{19}\ m^{-2}\)).

Galileo (1564—1642) (Galileo, Two New Sciences, traducción al inglés por H. Crew y A. de Salvio, The Macmillan Co., Nueva York, 1933. También véase S.P. Timoshenko, History of Strength of Materials, McGraw-Hill, Nueva York, 1953.) se dice que utilizó esta observación para señalar que los gigantes, si existieran, serían criaturas muy frágiles. Su fuerza sería mayor que la nuestra, ya que las áreas transversales de sus sistemas esquelético y muscular serían mayores por un factor relacionado con el cuadrado de su altura (denotado L en el famoso boceto DaVinci mostrado en la Figura 3). Pero su peso, y así las cargas que deben soportar, aumentarían a medida que su volumen, es decir por el cubo de su altura. Una simple caída probablemente les haría un gran daño. Por el contrario, la fuerza “proporcionada” del famoso arácnido mencionado semanalmente en la tira cómica de SpiderMan es en su mayoría justamente este mismo efecto de tamaño. No hay nada mágico en la fuerza muscular de los insectos, pero la proporción de\(L^2\) a\(L^3\) funciona a su favor cuando se cuenta la fuerza por peso corporal. Esto nos advierte que el simple escalado de un diseño previamente probado no es un procedimiento de diseño seguro. Un jet jumbo no es solo un plano pequeño escalado; si esto se hiciera, los componentes de carga serían demasiado pequeños en el área de la sección transversal para soportar las cargas mucho mayores que serían llamados a resistir.

Al reportar la resistencia de los materiales cargados en tensión, es costumbre dar cuenta de este efecto de área dividiendo la carga de rotura por el área de sección transversal:

\[\sigma_f = \dfrac{P_f}{A_0}\]

donde\(\sigma_f\) es el esfuerzo de tracción final, a menudo abreviado como UTS,\(P_f\) es la carga en la fractura, y\(A_0\) es el área de la sección transversal original. (Algunos materiales exhiben reducciones sustanciales en el área de la sección transversal a medida que se estiran, y el uso del área original en lugar del área final da la llamada fuerza de ingeniería). Las unidades de tensión son obviamente de carga por unidad de área,\(N/m^2\) (también llamadas Pascales, o Pa) en el sistema SI y\(lb/in^2\) (o psi) en unidades que todavía se utilizan comúnmente en los Estados Unidos.

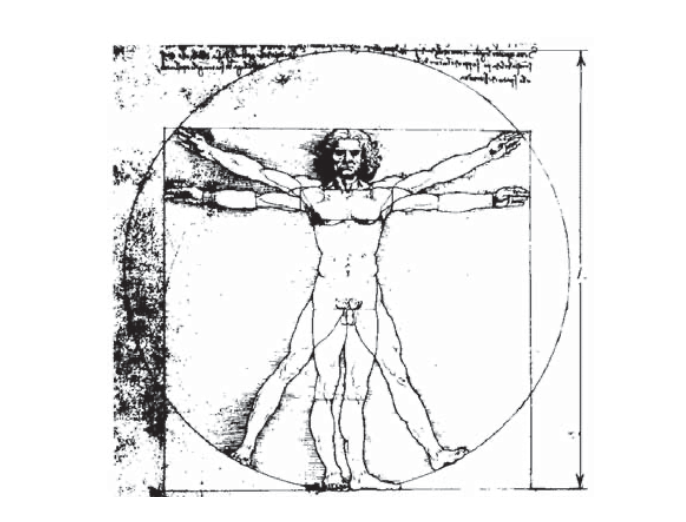
Figura 3: Balanzas de fuerza con\(L^2\), pero básculas de peso con\(L^3\).

Ejemplo\(\PageIndex{1}\)

En muchos problemas de diseño, las cargas a aplicar a la estructura son conocidas desde el principio, y deseamos calcular cuánto material se necesitará para soportarlas. Como un caso muy sencillo, digamos que deseamos utilizar una varilla de acero, circular en forma de sección transversal como se muestra en la Figura 4, para soportar una carga de 10,000 lb. ¿Cuál debe ser el diámetro de la varilla?

Figura 4: Varilla de acero que soporta un peso de 10,000 lb.

Directamente a partir de la Ecuación 1.1.1, el área\(A_0\) que estará justo al borde de la fractura a una carga dada\(P_f\) es

\[A_0 = \dfrac{P_f}{\sigma_f}\nonumber\]

Todo lo que necesitamos hacer es buscar el valor del\(\sigma_f\) material, y sustituirlo junto con el valor de 10,000 lb para\(P_f\), y el problema está resuelto.

Una serie de propiedades de los materiales se enumeran en el módulo Propiedades de los Materiales, donde encontramos que el UTS del acero al carbono es de 1200 MPa. También observamos que estas propiedades varían ampliamente para determinados materiales dependiendo de su composición y procesamiento, por lo que el valor de 1200 MPa es solo una estimación preliminar del diseño. A la luz de esa incertidumbre, y de muchas otras potenciales, es común incluir un “factor de seguridad” en el diseño. La selección de un factor apropiado es una elección a menudo difícil, especialmente en los casos en que las restricciones de peso o costo imponen una gran penalización al uso de exceso de material. Pero en este caso el acero es relativamente económico y no tenemos limitaciones especiales de peso, por lo que usaremos un factor de seguridad conservador del 50% y asumiremos que la resistencia a la tracción máxima es 1200/2 = 600 Mpa.

Ahora solo tenemos que ajustar las unidades antes de resolver por área. Los ingenieros deben sentirse muy cómodos con las conversiones de unidades, especialmente dada la combinación de SI y unidades tradicionales más antiguas utilizadas hoy en día. Eventualmente, probablemente pediremos varillas de acero usando pulgadas en lugar de metros, por lo que convertiremos el MPa a psi en lugar de convertir las libras a Newtons. También usando\(A = \pi d^2/4\) para calcular el diámetro en lugar del área, tenemos

\[d = \sqrt{\dfrac{4A}{\pi}} = \sqrt{\dfrac{4P_f}{\pi \sigma_f}} = \left[\dfrac{4 \times 10000 (lb)}{\pi \times 600 \times 10^6 (N/m^2) \times 1.449 \times 10^{-4} (\tfrac{lb/in^2}{N/m^2})}\right ]^{\tfrac{1}{2}} = 0.38\ in\nonumber\]

Probablemente no pediríamos varilla de exactamente 0.38 pulgadas, ya que eso sería de un tamaño extraño y por lo tanto demasiado caro. Pero\(3/8''\) (0.375 in) probablemente sería un tamaño estándar, y sería aceptable a la luz de nuestro factor de seguridad conservador.

Si el espécimen es cargado por una fuerza axial\(P\) menor que la carga de rotura\(P_f\), el esfuerzo de tracción se define por analogía con la Ecuación 1.1.1 como

\[\sigma = \dfrac{P}{A_0}\]

El esfuerzo de tracción, la fuerza por unidad de área que actúa sobre un plano transversal a la carga aplicada, es una medida fundamental de las fuerzas internas dentro del material. Gran parte de Mecánica de Materiales se ocupa de elaborar este concepto para incluir órdenes superiores de dimensionalidad, elaborar métodos para determinar la tensión para diversas geometrías y condiciones de carga, y predecir cuál será la respuesta del material a la tensión.

Ejemplo\(\PageIndex{2}\)

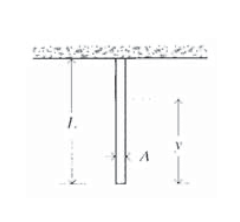
Figura 5: Varilla circular suspendida de la parte superior y portando su propio peso.

Muchas aplicaciones de ingeniería, especialmente los vehículos aeroespaciales, requieren materiales resistentes y livianos. Una medida de esta combinación de propiedades se proporciona calculando cuánto tiempo puede ser una varilla del material que cuando está suspendida de su parte superior se romperá por su propio peso (ver Figura 5). Aquí la tensión no es uniforme a lo largo de la varilla: el material en la parte superior lleva el peso de toda la varilla, pero que en la parte inferior no lleva ninguna carga en absoluto.

Para calcular la tensión en función de la posición, vamos a denotar y la distancia desde el fondo de la varilla y dejar que la densidad de peso del material, por ejemplo in\(N/m^3\), sea denotada por\(\gamma\). (La densidad de peso está relacionada con la densidad de masa\(\rho\)\([kg/m^3]\) por\(\gamma = \rho g\), donde\(g = 9.8 m/s^2\) está la aceleración debida a la gravedad.) El peso soportado por la sección transversal\(y\) es solo la densidad de peso\(\gamma\) multiplicada por el volumen de material\(V\) a continuación\(y\):

\[W(y) = \gamma V =\gamma Ay\nonumber\]

La tensión de tracción se da entonces como una función de\(y\) por la Ecuación 1.1.2 como

\[\sigma(y) = \dfrac{W(y)}{A} = \gamma y\]

Tenga en cuenta que el área se cancela, dejando solo la densidad del material\(\gamma\) como variable de diseño.

La longitud de la varilla que está justo a punto de romperse bajo su propio peso ahora se puede encontrar dejando\(y = L\) (la mayor tensión ocurre en la parte superior)\(\sigma (L) = \sigma_f\), fraguando y resolviendo\(L\):

\[\sigma_f = \gamma L \Rightarrow L = \dfrac{\sigma_f}{\gamma}\nonumber\]

En el caso del acero, encontramos que la densidad de masa\(\rho\) en el Apéndice A es\(7.85 \times 10^3 (kg/m^3)\); luego

\[L = \dfrac{\sigma_f}{\rho g} = \dfrac{1200 \times 10^6 (N/m^2)}{7.85 \times 10^3 (kg/m^3) \times 9.8 (m/s^2)} = 15.6\ km\nonumber\]

Esto sería de hecho una varilla larga; el propósito de tal cálculo no es tanto diseñar varillas superlargas como proporcionar una forma vívida de comparar materiales (ver Ejercicio\(\PageIndex{4}\)).

Rigidez

Es importante distinguir la rigidez, que es una medida de la carga necesaria para inducir una determinada deformación en el material, de la resistencia, que generalmente se refiere a la resistencia del material a la falla por fractura o deformación excesiva. La rigidez generalmente se mide aplicando cargas relativamente pequeñas, muy cortas de fractura, y midiendo la deformación resultante. Dado que las deformaciones en la mayoría de los materiales son muy pequeñas para estas condiciones de carga, el problema experimental es en gran medida el de medir pequeños cambios en la longitud con precisión.

Hooke (Robert Hooke (1635—1703) fue un contemporáneo y rival de Isaac Newton. Hooke fue un gran pionero en mecánica, pero competir con Newton no es fácil.) realizó una serie de tales mediciones en cables largos bajo diversas cargas, y observó que a una buena aproximación la carga\(P\) y su deformación resultante\(\delta\) se relacionaron linealmente siempre y cuando las cargas fueran suficientemente pequeño. Esta relación, generalmente conocida como Ley de Hooke, puede escribirse algebraicamente como

\[P = k\delta\]

donde\(k\) es una constante de proporcionalidad llamada rigidez y que tiene unidades de\(lb/in\) o\(N/m\). La rigidez definida por no\(k\) es una función del material solo, sino que también está influenciada por la forma del espécimen. Un cable da mucha más deflexión para una carga dada si se enrolla como un resorte de reloj, por ejemplo.

Una manera útil de ajustar la rigidez para que sea una propiedad puramente de materiales es normalizar la carga por el área de la sección transversal; es decir, usar la tensión de tracción en lugar de la carga. “Además, la deformación\(\delta\) puede normalizarse señalando que una carga aplicada estira todas las partes del alambre de manera uniforme, de modo que una medida razonable de “" estiramiento "” es la deformación por unidad de longitud:”

\[\epsilon = \dfrac{\delta}{L_0}\]

Aquí\(L_0\) está la longitud original y\(\epsilon\) es una medida adimensional de estiramiento llamada tensión. Utilizando estas medidas más generales de carga por unidad de superficie y desplazamiento por unidad de longitud (Al parecer, fue el matemático suizo Jakob Bernoulli (1655-1705) quien primero se dio cuenta de la exactitud de esta forma, publicada en el artículo final de su vida.), La Ley de Hooke se convierte en:

\[\dfrac{P}{A_0} = E\dfrac{\delta}{L_0}\]

o

\[\sigma = E\epsilon\]

La constante de proporcionalidad\(E\), llamada módulo de Young (After the English physicist Thomas Young (1773—1829), quien también hizo contribuciones notables a la subposición de la interferencia de la luz además de ser un destacado médico y egiptólogo.) o el módulo de elasticidad, es una de las más descriptores mecánicos importantes de un material. Cuenta con las mismas unidades que estrés, Pa o psi. Como se muestra en la Figura 6, la ley de Hooke puede referirse a cualquiera de las Eqns. 1.1.3 o 1.1.6.

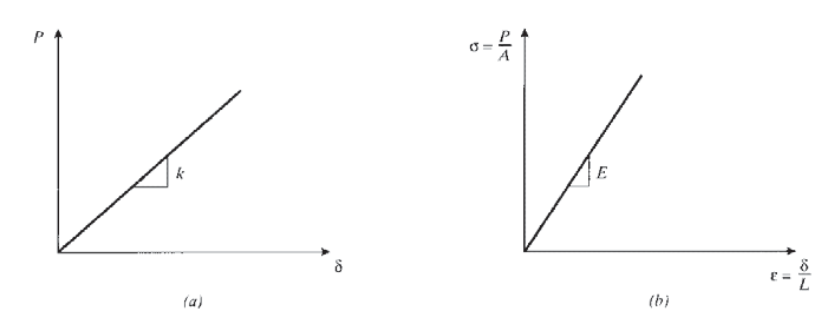
Figura 6: Ley de Hooke en términos de (a) carga-desplazamiento y (b) tensión-deformación.

La rigidez Hookean\(k\) es ahora reconocible como relacionada con el módulo de Young\(E\) y la geometría del espécimen como

\[k = \dfrac{AE}{L}\]

donde aquí se baja el subíndice 0 del área\(A\); se asumirá a partir de aquí (a menos que se indique lo contrario) que se puede descuidar el cambio de área durante la carga. Otra relación útil se obtiene resolviendo la Ecuación 1.1.5 para la deflexión en términos de la carga aplicada como

\[\delta = \dfrac{PL}{AE}\]

Tenga en cuenta que la tensión\(\sigma = P/A\) desarrollada en una muestra de tracción sometida a una carga fija es independiente de las propiedades del material, mientras que la deflexión depende de la propiedad del material\(E\). De ahí que la tensión\(\sigma\) en una muestra de tracción a una carga dada sea la misma ya sea de acero o polietileno, pero la deformación\(\epsilon\) sería diferente: el polietileno exhibirá una deformación y deformación mucho mayores, ya que su módulo es dos órdenes de magnitud menor que el del acero.

Ejemplo\(\PageIndex{3}\)

En Ejemplo\(\PageIndex{1}\), encontramos que una varilla\(0.38''\) de acero de diámetro soportaría de manera segura una carga de 10,000 lb Ahora supongamos que se nos ha dado un segundo objetivo de diseño, a saber, que la geometría requiere que usemos una varilla de 15 pies de longitud pero que no se puede permitir que el extremo cargado se desvíe hacia abajo más de \(0.3''\)cuando se aplica la carga. Sustituyendo\(A\) en la Ecuación 1.1.8 por\(\pi d^2/4\) y resolviendo para\(d\), el diámetro para un dado\(\delta\) es

\[d = 2 \sqrt{\dfrac{PL}{n\delta E}}\nonumber\]

Del Apéndice A, el módulo del acero al carbono es 210 GPa; usando esto junto con la carga, longitud y deflexión dadas, el diámetro requerido es

\[d = 2 \sqrt{\dfrac{10^4 (lb) \times 15 (ft) \times (in/ft)}{\pi \times 0.3 (in) \times 210 \times 10^9 (N/m^2) \times 1.449 \times 10^{-4} (\tfrac{lb/in^2}{N/m^2})}} = 0.5\ in \nonumber\]

Este diámetro es mayor que el 0.38′′ calculado anteriormente; por lo tanto, se debe usar una varilla más grande si se quiere cumplir la deflexión así como los objetivos de resistencia. Claramente, el uso de la varilla más grande hace que la tensión de tracción en el material sea menor y por lo tanto disminuye la probabilidad de fractura. Este es un ejemplo de un diseño crítico de rigidez, en el que la deflexión más que la fractura es la restricción gobernante. Como sucede, muchas estructuras a lo largo de la era moderna han sido diseñadas para la rigidez más que para la fuerza, y así terminadas siendo “sobrediseñadas” con respecto a la fractura. Esto, sin duda, ha disminuido la incidencia de catástrofes relacionadas con fracturas, las cuales serán atendidas en los módulos sobre fractura.

Ejemplo\(\PageIndex{4}\)

Figura 7: Deformación de una columna bajo su propio peso.

Cuando columnas muy largas están suspendidas de la parte superior, como en un cable que cuelga por el agujero de un pozo de petróleo, la deflexión debida al peso del material en sí puede ser importante. La solución para la deflexión total es una extensión menor de la Ecuación 1.1.8, en que ahora debemos considerar el peso creciente que soporta cada sección transversal a medida que aumenta la distancia desde el fondo del cable. Como se muestra en la Figura 7, el alargamiento total de una columna de longitud\(L\)\(A\), área de sección transversal y densidad de peso\(\gamma\) debido a su propio peso se puede encontrar considerando la deformación incremental\(d\delta\) de una rebanada dy a una\(y\) distancia del fondo. El peso que soporta esta rebanada es\(\gamma Ay\), entonces

\[d \delta = \dfrac{(\gamma Ay) dy}{AE}\nonumber\]

\[\delta = \int_{0}^{L} \ d\delta = \dfrac{\gamma}{E} \dfrac{y^2}{2} |_{0}^{L} = \dfrac{\gamma L^2}{2E}\nonumber\]

Tenga en cuenta que\(\delta\) es independiente del área\(A\), por lo que encontrar un cable más grueso no ayudará a reducir la deformación; el parámetro crítico es el módulo específico\(E/\gamma\). Dado que el peso total es\(W = \gamma AL\), el resultado también se puede escribir

\[\delta = \dfrac{WL}{2AE}\nonumber\]

La deformación es la misma que en una barra que se tira con una fuerza de tracción igual a la mitad de su peso; esto es solo la fuerza promedio que experimentan las secciones transversales a lo largo de la columna.

En Ejemplo\(\PageIndex{2}\), calculamos la longitud de una varilla de acero que estaría justo a punto de romperse bajo su propio peso si se suspendiera de su parte superior; obtuvimos\(L = 15.6\) km. Si se construyera tal varilla, nuestro análisis predice que la deformación en la parte inferior sería

\[\delta = \dfrac{\gamma L^2}{2E} = \dfrac{7.85 \times 10^3 (kg/m^3) \times 9.8 (m/s^2) \times [15.6 \times 10^3 (m)]^2}{2 \times 210 times 10^9 (N/m^2)} = 44.6 \ m\nonumber\]

Sin embargo, este análisis asume que la ley de Hooke se mantiene en todo el rango de tensiones desde cero hasta fractura. Esto no es cierto para muchos materiales, incluido el acero al carbono, y los módulos posteriores abordarán la respuesta de los materiales a altas tensiones.

Un material que obedece a la Ley de Hooke (Ecuación 1.1.6) se llama Hookean. Dicho material es elástico de acuerdo con la descripción de elasticidad dada en la introducción (respuesta inmediata, recuperación completa), y también es lineal en su relación entre tensión y deformación (o equivalentemente, fuerza y deformación). Por lo tanto, un material Hookean es elástico lineal, y los ingenieros de materiales utilizan estos descriptores indistintamente. Es importante tener en cuenta que no todos los materiales elásticos son lineales (el caucho es elástico pero no lineal), y no todos los materiales lineales son elásticos (los materiales viscoelásticos pueden ser lineales en el sentido matemático, pero no responden inmediatamente y por lo tanto no son elásticos).

La proporcionalidad lineal entre el estrés y la tensión dada por la ley de Hooke no es tan general como, digamos, la teoría general de la relatividad de Einstein, o incluso la ley de la gravitación de Newton. Realmente es solo una aproximación que se observa que es razonablemente válida para muchos materiales siempre que las tensiones aplicadas no sean demasiado grandes. A medida que aumentan las tensiones, eventualmente se observará una respuesta material más complicada. Algunos de estos efectos se detallarán en el Módulo sobre Curvas de Estrés-Tensión, que introduce la medición experimental de la respuesta a la deformación de los materiales en un rango de tensiones hasta e incluyendo la fractura.

Si tuviéramos que empujar el espécimen en lugar de tirar de él, la carga se describiría como compresiva en lugar de extensible. En el rango de cargas relativamente bajas, la ley de Hooke también se sostiene para este caso. Por convención, las tensiones de compresión y las tensiones son negativas, por lo que la expresión se\(\sigma = E\epsilon\) mantiene tanto para la tensión como para la compresión.

Ejercicio\(\PageIndex{1}\)

Determinar la tensión y deformación total de un alambre de aluminio, de 30 m de largo y 5 mm de diámetro, sometido a una carga axial de 250 N.

Ejercicio\(\PageIndex{2}\)

Dos varillas, una de nylon y otra de acero, están rígidamente conectadas como se muestra. Determinar las tensiones y deformaciones axiales cuando se aplica una carga axial de\(F = 1\) kN.

Ejercicio\(\PageIndex{3}\)

Un cable de acero de 10 mm de diámetro y 1 km de largo soporta una carga además de su propio peso de\(W\) = 150 N. Encuentra el alargamiento total del cable.

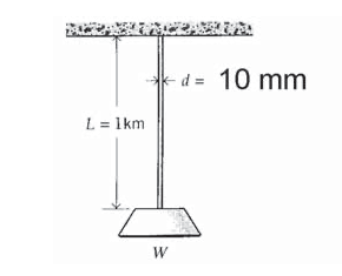
Ejercicio\(\PageIndex{4}\)

Utilizando los valores numéricos dados en el Módulo sobre Propiedades del Material,, clasificar los materiales dados en términos de la longitud de la varilla que apenas soportará su propio peso.

Ejercicio\(\PageIndex{5}\)

Trazar las longitudes máximas de varilla autoportantes de los materiales en Ejercicio\(\PageIndex{4}\) versus el costo (por unidad de área transversal) de la varilla.

Ejercicio\(\PageIndex{6}\)

Demostrar que la rigidez efectiva de dos muelles conectados en (a) serie y (b) paralelo es

(a) serie:\(\dfrac{1}{k_{eff}} = \dfrac{1}{k_1} + \dfrac{1}{k_2}\)

b) paralelo:\(k_{eff} = k_1 + k_2\)

(Obsérvese que éstas son la inversa de las relaciones para la resistencia eléctrica efectiva de dos resistencias conectadas en serie y en paralelo, que utilizan los mismos símbolos).

Ejercicio\(\PageIndex{7}\)

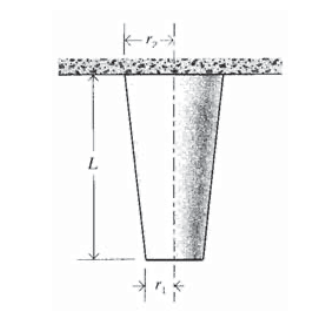
Una columna cónica de módulo\(E\) y densidad de masa\(\rho\) varía linealmente desde un radio de\(r_1\) hasta\(r_2\) en una longitud\(L\). Encuentra la deformación total causada por una carga axial\(P\).

Ejercicio\(\PageIndex{8}\)

Una columna cónica de módulo\(E\) y densidad de masa\(\rho\) varía linealmente desde un radio de\(r_1\) hasta\(r_2\) en una longitud\(L\), y está colgando de su extremo ancho. Encuentra la deformación total debido al peso de la barra.

Ejercicio\(\PageIndex{9}\)

Una varilla de sección transversal circular cuelga bajo la influencia de su propio peso, y además tiene una carga axial\(P\) suspendida de su extremo libre. Determinar la forma de la barra, es decir, la función\(r(y)\) tal que la tensión axial sea constante a lo largo de la longitud de la barra.

Ejercicio\(\PageIndex{10}\)

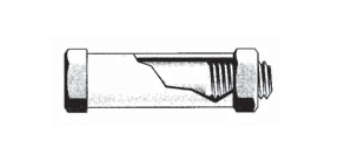
Un perno con 20 roscas por pulgada pasa a través de un manguito y una tuerca se enrosca sobre el perno como se muestra. Luego se aprieta la tuerca media vuelta más allá de la tensión con los dedos; encuentra las tensiones en el perno y el manguito. Todos los materiales son de acero, el área de la sección transversal del perno es\(0.5 \ in^2\), y el área del manguito es\(0.4 \ in^2\).