1.4: Curvas de esfuerzo-deformación
- Page ID
- 83342
Introducción
Las curvas de tensión-deformación son una medida gráfica extremadamente importante de las propiedades mecánicas de un material, y todos los estudiantes de Mecánica de Materiales las encontrarán a menudo. Sin embargo, no carecen de cierta sutileza, especialmente en el caso de materiales dúctiles que pueden sufrir cambios geométricos subestantiales durante las pruebas. Este módulo proporcionará una discusión introductoria de varios puntos necesarios para interpretar estas curvas, y al hacerlo también proporcionará una visión preliminar de varios aspectos de las propiedades mecánicas de un material. Sin embargo, este módulo no intentará examinar la amplia gama de curvas de tensión-deformación exhibidas por los materiales de ingeniería modernos (para ello se puede consultar el atlas de Boyer citado en la sección Referencias). Varios de los temas que aquí se mencionan —especialmente el rendimiento y la fractura— aparecerán con más detalle en los módulos posteriores.
Curvas de esfuerzo-deformación de “ingeniería”
Quizás la prueba más importante de la respuesta mecánica de un material es la prueba de tracción (la prueba de esfuerzo y deformación, así como casi todos los procedimientos experimentales en mecánica de materiales, es detallada por organizaciones que establecen estándares, notablemente la Sociedad Americana de Pruebas y Materiales (ASTM). Las pruebas de tracción de metales están prescritas por la Prueba ASTM E8, los plásticos por ASTM D638 y los materiales compuestos por ASTM D3039.), en los que un extremo de una muestra de varilla o alambre se sujeta en un marco de carga y el otro se somete a un desplazamiento controlado\(\delta\) (ver Figura 1). Un transductor conectado en serie con la muestra proporciona una lectura electrónica de la carga\(P (\delta)\) correspondiente al desplazamiento. Alternativamente, las modernas máquinas de prueba servocontroladas permiten usar carga en lugar de desplazamiento como variable controlada, en cuyo caso el desplazamiento\(\delta (P)\) sería monitoreado en función de la carga.
Las medidas de ingeniería de esfuerzo y deformación, denotadas en este módulo como σe y εe respectivamente, se determinan a partir de la medición de la carga y deflexión utilizando el área\(A_0\) de sección transversal y la longitud del espécimen original\(L_0\) como
\[\sigma_e = \dfrac{P}{A_0}, \epsilon_e = \dfrac{\delta}{L_0}\]
Cuando se representa la tensión σe frente a la deformación\(\epsilon_e\), se obtiene una curva de ingeniería tensión-deformación como la que se muestra en la Figura 2.


En la parte temprana (baja deformación) de la curva, muchos materiales obedecen la ley de Hooke a una aproximación razonable, de manera que la tensión es proporcional a la deformación siendo la constante de proporcionalidad el módulo de elasticidad o el módulo de Young, denotado\(E\):
\[\sigma_e = E_{\epsilon_e}\]
A medida que aumenta la deformación, muchos materiales eventualmente se desvían de esta proporcionalidad lineal, denominándose el punto de partida el límite proporcional. Esta no linealidad suele estar tan sociada con el flujo “plástico” inducido por estrés en el espécimen. Aquí el material está experimentando un reordenamiento de su estructura molecular o microscópica interna, en la que los átomos están siendo trasladados a nuevas posiciones de equilibrio. Esta plasticidad requiere un mecanismo para la movilidad molecular, que en los materiales cristalinos puede surgir del movimiento de dislocación (discutido más adelante en un módulo posterior). Los materiales que carecen de esta movilidad, por ejemplo al tener microestructuras internas que bloquean el movimiento de dislocación, suelen ser frágiles en lugar de dúctiles. La curva de tensión-deformación para materiales frágiles es típicamente lineal en todo su rango de deformación, terminando finalmente en fractura sin un flujo de plástico apreciable.
Obsérvese en la Figura 2 que la tensión necesaria para aumentar la deformación más allá del límite proporcional en un material dúctil continúa aumentando más allá del límite proporcional; el material requiere una tensión cada vez mayor para continuar con la deformación, un mecanismo denominado endurecimiento por deformación.
Estos reordenamientos microestructurales asociados con el flujo de plástico generalmente no se invierten cuando se retira la carga, por lo que el límite proporcional suele ser el mismo o al menos cercano al límite elástico de los materiales. La elasticidad es la propiedad de una recuperación completa e inmediata de un desplazamiento impuesto al liberar la carga, y el límite elástico es el valor de la tensión en la que el material experimenta una deformación residual permanente que no se pierde al descargar. La deformación residual inducida por una tensión dada se puede determinar dibujando una línea de descarga desde el punto más alto alcanzado en la curva se - ee en esa tensión de regreso al eje de deformación, dibujada con una pendiente igual a la de la línea de carga elástica inicial. Esto se hace porque el material se descarga elásticamente, no existiendo ninguna fuerza impulsando la estructura molecular de nuevo a su posición original.
Un término estrechamente relacionado es el límite elástico, denotado\(\sigma_Y\) en estos módulos; este es el esfuerzo necesario para inducir la deformación plástica en el espécimen. Dado que a menudo es difícil determinar la tensión exacta a la que comienza la deformación plástica, a menudo se considera que el límite elástico es el esfuerzo necesario para inducir una cantidad específica de deformación permanente, típicamente 0.2%. La construcción utilizada para encontrar este “límite elástico compensado” se muestra en la Figura 2, en la que\(E\) se dibuja una línea de pendiente desde el eje de deformación a\(\epsilon_e\) = 0.2%; esta es la línea de descarga que resultaría en la deformación permanente especificada. El esfuerzo en el punto de intersección con la\(\sigma_e - \epsilon_e\) curva es el límite elástico compensado.
La Figura 3 muestra la curva de ingeniería tensión-deformación para cobre con una escala ampliada, mostrando ahora deformaciones desde cero hasta fractura de espécimen. Aquí aparece que la tasa de endurecimiento por deformación (La tasa de endurecimiento por deformación es la pendiente de la curva de tensión-deformación, también llamada módulo tangente.) disminuye hasta un punto etiquetado UTS, para la Resistencia a la Tensión Última (denotada σf en estos módulos). Más allá de ese punto, el material parece ablandarse por deformación, de modo que cada incremento de tensión adicional requiere una tensión menor.

El cambio aparente de endurecimiento por deformación a ablandamiento por deformación es un artefacto del procedimiento de trazado, sin embargo, como es el máximo observado en la curva en la UTS. Más allá del límite de elasticidad, el flujo molecular provoca una reducción sustancial en el área de la sección transversal de la muestra\(A\), por lo que el verdadero esfuerzo\(\sigma_t = P/A\) realmente soportado por el material es mayor que el esfuerzo de ingeniería calculado a partir del área de sección transversal original (\(\sigma_e = P/A_0\)). La carga debe ser igual al esfuerzo verdadero por el área real (\(P = \sigma_t A\)), y siempre y cuando el endurecimiento por deformación pueda aumentar\(\sigma_t\) lo suficiente como para compensar el área reducida\(A\), la carga y por lo tanto la tensión de ingeniería continuarán aumentando a medida que aumente la deformación. Eventualmente, sin embargo, la disminución del área debido al flujo se vuelve mayor que el aumento de la tensión real debido al endurecimiento por deformación, y la carga comienza a caer. Este es un efecto geométrico, y si se trazara la tensión verdadera en lugar de la tensión de ingeniería, no se observaría ningún máximo en la curva.
En la UTS el diferencial de la carga\(P\) es cero, dando una relación analítica entre la tensión verdadera y el área en el cuello:
\[P = \sigma_t A \to dP = 0 = \sigma_t dA + A d \sigma_t \to -\dfrac{dA}{A} = \dfrac{d\sigma_t}{\sigma_t}\]
La última expresión establece que la carga y por lo tanto la tensión de ingeniería alcanzarán un máximo en función de la deformación cuando la disminución fraccionaria en el área sea igual al aumento fraccional de la tensión verdadera.
Aunque el UTS es quizás la propiedad de los materiales más comúnmente reportada en las pruebas de tracción, no es una medida directa del material debido a la influencia de la geometría como se discutió anteriormente, y debe usarse con precaución. El límite elástico σY es generalmente preferido al UTS en el diseño con metales dúctiles, aunque el UTS es un criterio de diseño válido para materiales quebradizos que no presentan estas reducciones inducidas por flujo en el área transversal.
El verdadero estrés no es del todo uniforme en todo el espécimen, y siempre habrá alguna ubicación -quizás una mella o algún otro defecto en la superficie- donde la tensión local sea máxima. Una vez que se ha alcanzado el máximo en la curva de ingeniería, el flujo localizado en este sitio no puede compensarse con un mayor endurecimiento por deformación, por lo que el área allí se reduce aún más. Esto aumenta aún más el estrés local, lo que acelera aún más el flujo. Este flujo localizado y creciente pronto conduce a un “cuello” en la longitud del calibre del espécimen como el que se ve en la Figura 4.

Hasta que se forma el cuello, la deformación es esencialmente uniforme en todo el espécimen, pero después del estrechamiento toda la deformación posterior tiene lugar en el cuello. El cuello se vuelve cada vez más pequeño, el verdadero estrés local aumenta todo el tiempo, hasta que el espécimen falla. Este será el modo de falla para la mayoría de los metales dúctiles. A medida que el cuello se contrae, la geometría no uniforme altera el estado de tensión uniaxial a uno complejo que involucra componentes de cizallamiento así como tensiones normales. El espécimen suele fallar finalmente con una geometría de “copa y cono” como se ve en la Figura 5, en la que las regiones exteriores fallan en cizallamiento y el interior en tensión. Cuando el espécimen se fractura, la deformación de ingeniería a la rotura,\(\epsilon_f\) denotada, incluirá la deformación en la región del cuello y la región sin cuello juntas. Dado que la verdadera deformación en el cuello es mayor que la del material sin cuello, el valor de\(\epsilon_f\) dependerá de la fracción de la longitud del calibre que haya estrechado. Por lo tanto,\(\epsilon_f\) es una función tanto de la geometría del espécimen como del material, y por lo tanto es solo una medida cruda de la ductilidad del material.

La Figura 6 muestra la curva de ingeniería tensión-deformación para un termoplástico semicristalino. La respuesta de este material es similar a la del cobre que se ve en la Figura 3, en que muestra un límite proporcional seguido de un máximo en la curva en la que se produce el estrechamiento. (Es común denominar este máximo como el límite elástico en los plásticos, aunque el flujo de plástico en realidad ha comenzado con deformaciones anteriores).

El polímero, sin embargo, difiere dramáticamente del cobre en que el cuello no continúa encogiéndose hasta que falla el espécimen. Más bien, el material en el cuello se estira solo a una “relación de estiramiento natural” que es una función de la temperatura y el procesamiento de la muestra, más allá de lo cual el material en el cuello deja de estirarse y el nuevo material en el cuello hombros cuellos hacia abajo. Luego, el cuello se propaga hasta que abarca toda la longitud del calibre del espécimen, un proceso llamado dibujo. Este proceso se puede observar sin necesidad de una máquina de prueba, estirando un “soporte de seis paquetes” de polietileno, como se ve en la Figura 7.
No todos los polímeros son capaces de sostener este proceso de estirado. Como se discutirá en la siguiente sección, ocurre cuando el proceso de formación de cuello produce una microestructura fortalecida cuya carga de rotura es mayor que la necesaria para inducir el estrechamiento en el material no transformado justo fuera del cuello.

Curvas “verdaderas” de tensión-deformación
Como se discutió en el apartado anterior, la curva de ingeniería tensión-deformación debe interpretarse con precaución más allá del límite elástico, ya que las dimensiones de la muestra experimentan un cambio sustancial con respecto a sus valores originales. El uso de la tensión verdadera\(\sigma_t = P/A\) en lugar de la tensión de ingeniería\(\sigma_e = P/A_0\) puede dar una medida más directa de la respuesta del material en el rango de flujo de plástico. Una medida de deformación utilizada a menudo junto con la tensión verdadera toma el incremento de deformación para ser el incremento incremental en el desplazamiento dL dividido por la longitud actual\(L\):
\[d \epsilon_t = \dfrac{dL}{l} \to \epsilon_t = \int_{l_0}^{L} \dfrac{1}{L} dL = \ln \dfrac{L}{L_0}\]
A esto se le llama la cepa “verdadera” o “logarítmica”.
Durante el rendimiento y el régimen de flujo de plástico después del rendimiento, el material fluye con un cambio insignificante en el volumen; los aumentos en la longitud se compensan por disminuciones en el área de la sección transversal. Antes del estrechamiento, cuando la deformación sigue siendo uniforme a lo largo de la longitud de la muestra, esta restricción de volumen se puede escribir:
\[dV = 0 \to AL = A_0 L_0 \to \dfrac{L}{L_0} =\dfrac{A}{A_0}\]
La relación\(L/L_0\) es la relación de extensión, denotada como\(\lambda\). Usando estas relaciones, es fácil desarrollar relaciones entre las medidas verdaderas y de ingeniería de tensión y tensión (ver Ejercicio\(\PageIndex{2}\)):
\[\sigma_1 = \sigma_e (1 + \epsilon_e) = \sigma_e \lambda, \epsilon_t = \ln (1 + \epsilon_e) =\ln \lambda\]
Estas ecuaciones se pueden utilizar para derivar la verdadera curva de esfuerzo-deformación a partir de la curva de ingeniería, hasta la deformación en la que comienza el estrechamiento. La Figura 8 es un retrazado de la Figura 3, con la verdadera curva tensión-deformación calculada por este procedimiento agregada para su comparación.
Más allá del estrechamiento, la deformación no es uniforme en la longitud de la galga y calcular la verdadera curva tensión-deformación para mayores deformaciones de ingeniería no sería significativo. Sin embargo, se podría dibujar una curva completa de tensión-deformación verdadera si se monitoreara el área del cuello a lo largo de la prueba de tracción, ya que para la deformación logarítmica tenemos
\[\dfrac{L}{L_0} = \dfrac{A}{A_0} \to \epsilon_t = \ln \dfrac{L}{L_0} = \ln \dfrac{A}{A_0}\]
Los metales dúctiles a menudo tienen verdaderas relaciones esfuerzo-deformación que pueden describirse mediante una simple relación poder-ley de la forma:

\[\sigma_t = A\epsilon_t^n \to \log \sigma_t = \log A + n \log \epsilon_t\]
La Figura 9 es una gráfica logarítmica de los datos verdaderos de tensión-deformación (Aquí se utilizó el porcentaje de deformación\(\epsilon_t\); esto produce el mismo valor para\(n\) pero un valor\(A\) diferente a si se utilizaron valores completos en lugar de porcentajes) para el cobre de la Figura 8 que demuestra esta relación. Aquí el parámetro\(n = 0.474\) se denomina parámetro de endurecimiento por deformación, útil como medida de la resistencia al estrechamiento. Los metales dúctiles a temperatura ambiente suelen exhibir valores\(n\) de 0.02 a 0.5.

Un método gráfico conocido como la “construcción consid`ere” utiliza una forma de la verdadera curva de esfuerzo-deformación para cuantificar las diferencias en el estrechamiento y el dibujo de material a material. Este método vuelve a trazar la curva tensión-deformación con la tensión verdadera\(\sigma_t\) como la ordenada y la relación de extensión\(\lambda = L/L_0\) como abscisa. A partir de la Ecuación 1.4.6, la tensión de ingeniería\(\sigma_e\) correspondiente a cualquier valor de la tensión verdadera\(\sigma_t\) es la pendiente de una línea secante dibujada desde el origen (\(\lambda = 0\), no\(\lambda = 1\)) para intersectar la\(\sigma_t - \lambda\) curva en\(\sigma_t\).

Entre las muchas formas posibles que podrían asumir las verdaderas curvas tensión-deformación, consideremos las formas cóncavas hacia arriba, cóncavas hacia abajo y sigmoidales que se muestran en la Figura 10. Estos difieren en el número de puntos tangentes que se pueden encontrar para la línea secante, y producen las siguientes características de rendimiento:
(a) Sin tangentes: Aquí la curva siempre es cóncava hacia arriba como en la parte (a) de la Figura 10, por lo que la pendiente de la línea secante se eleva continuamente. Por lo tanto, el esfuerzo de ingeniería también aumenta, sin mostrar una caída de rendimiento. Eventualmente la fractura intercede, por lo que una verdadera curva de tensión-deformación de esta forma identifica un material que se fractura antes de que ceda.
(b) Una tangente: La curva es cóncava hacia abajo como en la parte (b) de la Figura 10, por lo que una línea secante alcanza un punto tangente en\(\lambda = \lambda_Y\). La pendiente de la línea secante, y por lo tanto también la tensión de ingeniería, comienza a caer en este punto. Este es entonces el límite elástico σY visto como un máximo en tensión en una curva convencional de tensión-deformación, y\(\lambda_Y\) es la relación de extensión en el rendimiento. El proceso de producción comienza en alguna ubicación adventicia en la longitud del calibre de la muestra, y continúa en esa ubicación en lugar de iniciarse en otra parte porque el módulo secante se ha reducido en la primera ubicación. El espécimen ahora fluye en una sola ubicación con resistencia decreciente, lo que finalmente conduce al fracaso. Los metales dúctiles como el aluminio fallan de esta manera, mostrando una marcada reducción en el área de la sección transversal en la posición de rendimiento y eventual fractura.
(c) Dos tangentes: Para las curvas sigmoidales de tensión-deformación como en la parte (c) de la Figura 10, la tensión de ingeniería comienza a caer en una ración de extensión\(\lambda_Y\), pero luego vuelve a subir a\(\lambda_d\). Al igual que en el caso previo de una tangente, el material comienza a ceder en una sola posición cuando\(\lambda = \lambda_Y\), produciendo un cuello que a su vez implica una distribución no uniforme de la tensión a lo largo de la longitud del calibre. El material en la ubicación del cuello luego se estira hasta\(\lambda_d\), después de lo cual la tensión de ingeniería allí tendría que elevarse para estirarlo aún más. Pero este estrés es mayor que el necesario para estirar el material en el borde del cuello desde\(\lambda_Y\) hasta\(\lambda_d\), por lo que el material que ya está en el cuello deja de estirarse y el cuello se propaga hacia afuera desde la ubicación de rendimiento inicial. Solo el material dentro de los hombros del cuello se estira durante la propagación, con el material dentro de la región estrechada manteniéndose constante en\(\lambda_d\), la “relación de estiramiento natural” del material, y el material exterior sujetándose en\(\lambda_Y\). Cuando todo el material ha sido arrastrado hacia la región de cuello, la tensión comienza a elevarse uniformemente en el espécimen hasta que finalmente se produce la fractura.
El aumento en la velocidad de endurecimiento por deformación necesaria para sostener el proceso de estirado en polímeros semicristalinos surge de una transformación dramática en la microestructura del material. Estos materiales son inicialmente “esferulíticos”, conteniendo placas cristalinas laminares planas, tal vez de 10 nm de espesor, dispuestas radialmente hacia afuera en un dominio esférico. A medida que aumenta la deformación inducida, estas esferulitas se deforman primero en la dirección de deformación. A medida que la tensión aumenta aún más, las esferulitas se rompen y los fragmentos laminares se reordenan con una orientación molecular predominantemente axial para convertirse en lo que se conoce como la microestructura fibrilar. Con los fuertes enlaces covalentes ahora dominantemente alineados en la dirección de carga, el material exhibe resistencias y rigideces notablemente mayores —quizás en un orden de magnitud— que en el material original. Esta estructura requiere una tasa de endurecimiento por deformación mucho mayor para aumentar la deformación, lo que provoca el repunte y la segunda tangente en la verdadera curva de tensión-deformación.
Energía de tensión
El área bajo la\(\sigma_e - \epsilon_e\) curva hasta un valor dado de deformación es la energía mecánica total por unidad de volumen consumida por el material al colarlo a ese valor. Esto se muestra fácilmente de la siguiente manera:
\[U^* = \dfrac{1}{V} \int P\ dL = \int_0^L \dfrac{P}{A_0} \dfrac{dL}{L_0} = \int_{0}^{\epsilon} \sigma d\epsilon\]
En ausencia de deslizamiento molecular y otros mecanismos para la disipación de energía, esta energía mecánica se almacena reversiblemente dentro del material como energía de deformación. Cuando las tensiones son lo suficientemente bajas como para que el material permanezca en el rango elástico, la energía de deformación es solo el área triangular en la Figura 11:

Tenga en cuenta que la energía de deformación aumenta cuadráticamente con la tensión o deformación; es decir, que a medida que aumenta la tensión, la energía almacenada por un incremento dado de tensión adicional crece a medida que el cuadrado de la cepa. Esto tiene consecuencias importantes, un ejemplo es que un arco de tiro con arco no puede ser simplemente una pieza curvada de madera para funcionar bien. Un arco real es inicialmente recto, luego doblado cuando se ensancha; esto almacena energía de tensión sustancial en él. Cuando se inclina más en dibujar la flecha hacia atrás, la energía disponible para lanzar la flecha es mucho mayor que si el arco estuviera simplemente tallado en forma curva sin doblarlo realmente.
La Figura 12 muestra esquemáticamente la cantidad de energía de deformación disponible para dos incrementos iguales de deformación\(\Delta_{\epsilon}\), aplicada a diferentes niveles de deformación existente.

| Material | Tensión máxima,% | Tensión máxima, MPa | Módulo de Dureza,\(MJ/m^3\) | Densidad\(kg/m^3\) | Máx. Energía\(J/kg\) |
| Hierro Antiguo | 0.03 | 70 | 0.01 | 7,800 | 1.3 |
| Acero moderno para muelles | 0.3 | 700 | 1.0 | 7,800 | 130 |
| Madera de tejo | 0.3 | 120 | 0.5 | 600 | 900 |
| Tendón | 8.0 | 70 | 2.8 | 1,100 | 2,500 |
| Caucho | 300 | 7 | 10.0 | 1,200 | 8,000 |
El área hasta el límite de elasticidad se denomina módulo de resiliencia, y el área total hasta la fractura se denomina módulo de tenacidad; estos se muestran en la Figura 13. El término “módulo” se utiliza porque las unidades de energía de deformación por unidad de volumen son\(N-m/m^3\) o\(N/m^2\), que son las mismas que tensión o módulo de elasticidad. El término “resiliencia” alude al concepto de que hasta el punto de ceder, el material no se ve afectado por la tensión aplicada y al descargar volverá a su forma original. Pero cuando la deformación excede el límite de fluencia, el material se deforma irreversiblemente, de manera que alguna deformación residual persistirá incluso después de la descarga. El módulo de resiliencia es entonces la cantidad de energía que el material puede absorber sin sufrir daños. Del mismo modo, el módulo de tenacidad es la energía necesaria para fracturar completamente el material. Los materiales que muestran buena resistencia al impacto son generalmente aquellos con altos módulos de tenacidad.

En el Cuadro 1 (J.E. Gordon, Structures, or Why Things Don't Fall Down, Plenum Press, Nueva York, 1978) se enumeran los valores de absorción de energía para una serie de materiales comunes. Tenga en cuenta que los materiales naturales y poliméricos pueden proporcionar una absorción de energía extremadamente alta por unidad de peso.
Durante la carga, el área bajo la curva tensión-deformación es la energía de deformación por unidad de volumen absorbida por el material. Por el contrario, el área bajo la curva de descarga es la energía liberada por el material. En el rango elástico, estas áreas son iguales y no se absorbe energía neta. Pero si el material se carga en el rango plástico como se muestra en la Figura 14, la energía absorbida supera la energía liberada y la diferencia se disipa como calor.

Compresión
La discusión anterior se refiere principalmente a la tensión simple, es decir, la carga uniaxial que aumenta el espaciamiento interatómico. Sin embargo, siempre y cuando las cargas sean suficientemente pequeñas (tensiones menores que el límite proporcional), en muchos materiales las relaciones descritas anteriormente se aplican igualmente bien si las cargas se colocan para poner la muestra en compresión en lugar de tensión. La expresión para deformación y una carga dada\(\delta = PL/AE\) se aplica igual que en tensión, con valores negativos para\(\delta\) e\(P\) indicando compresión. Además, el módulo\(E\) es el mismo en tensión y compresión a una buena aproximación, y la curva tensión-deformación simplemente se extiende como una línea recta hacia el tercer cuadrante como se muestra en la Figura 15.

Existen algunas dificultades prácticas para realizar pruebas de tensión-deformación en compresión. Si se aplican erróneamente cargas excesivamente grandes en una prueba de tracción, tal vez por ajustes incorrectos en la máquina de prueba, la muestra simplemente se rompe y la prueba debe repetirse con una nueva muestra. Pero en la compresión, un error puede dañar fácilmente la célula de carga u otros componentes sensibles, ya que incluso después de la falla de la muestra las cargas no se alivian necesariamente.
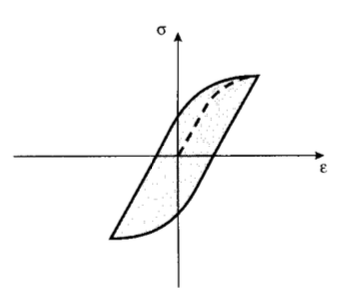
Las muestras cargadas cíclicamente para alternar entre tensión y compresión pueden exhibir bucles de histéresis si las cargas son lo suficientemente altas como para inducir flujo de plástico (tensiones por encima del límite elástico). El área encerrada en el bucle que se ve en la Figura 16 es la energía de deformación por unidad de volumen liberada como calor en cada ciclo de carga. Esta es la tendencia bien conocida de un alambre que se dobla hacia adelante y hacia atrás para calentarse bastante en la región de flexión plástica. La temperatura de la muestra aumentará de acuerdo con la magnitud de esta generación de calor interno y la velocidad a la que el calor puede eliminarse por conducción dentro del material y convección desde la superficie del espécimen.
La falla de la muestra por agrietamiento se inhibe en la compresión, ya que las grietas se cerrarán en lugar de abrirse por el estado de tensión. Una serie de materiales importantes son mucho más fuertes en compresión que en tensión por esta razón. El concreto, por ejemplo, tiene una buena resistencia a la compresión y por lo tanto encuentra un uso extensivo en la construcción en la que las tensiones dominantes son compresivas. Pero esencialmente no tiene resistencia en tensión, como lo atestiguan las grietas en las aceras y los cimientos de edificios: las tensiones de tracción aparecen a medida que estas estructuras se asientan, y las grietas comienzan con una tensión de tracción muy baja en el concreto no reforzado.
Referencias
- Boyer, H.F., Atlas de curvas de esfuerzo-deformación, ASM International, Metals Park, Ohio, 1987.
- Courtney, T.H., Comportamiento mecánico de materiales, McGraw-Hill, Nueva York, 1990.
- Hayden, H.W., W.G. Moffatt y J. Wulff, La estructura y propiedades de los materiales: Vol. III Comportamiento Mecánico, Wiley, Nueva York, 1965.
Ejercicio\(\PageIndex{1}\)
La siguiente figura muestra la curva de ingeniería esfuerzo-deformación para alu- minum policristalino puro; los datos numéricos para esta figura están en el archivo aluminum.txt, el cual puede ser importado a una hoja de cálculo u otro software de análisis. Para este material, determinar (a) el módulo de Young, (b) el límite elástico compensado de 0.2%, (c) la Resistencia a la Tensión Última (UTS), (d) el módulo de resiliencia y (e) el módulo de tenacidad.

Ejercicio\(\PageIndex{2}\)
Desarrollar las relaciones dadas en la Ecuación 1.4.6:
\[\sigma_t = \sigma_e (1 + \epsilon_e) =\sigma_e \lambda, \epsilon_t = \ln (1 + \epsilon_e) = \ln \lambda \nonumber\]
Ejercicio\(\PageIndex{3}\)
Usando las relaciones de la Ecuación 1.4.6, graficar la verdadera curva de esfuerzo-deformación para aluminio (usando datos de Ejercicio\(\PageIndex{1}\)) hasta la deformación de la formación del cuello.
Ejercicio\(\PageIndex{4}\)
Regraficar los resultados del problema anterior usando ejes log-log como en la Figura 9 para determinar los parámetros\(A\) y\(n\) en la Ecuación 1.4.8 para aluminio.
Ejercicio\(\PageIndex{5}\)
Usando la Ecuación 1.4.8 con parámetros\(A\) = 800 MPa,\(n = 0.2\), graficar la curva de esfuerzo-deformación de ingeniería hasta una deformación de\(\epsilon_e = 0.4\). ¿El material del cuello? Explique por qué la curva es o no es válida en cepas más allá del cuello.
Ejercicio\(\PageIndex{6}\)
Usando los parámetros del problema anterior, use la condición\((d\sigma_e/d\epsilon_e)_{\text{neck}} = 0 to show that the engineering strain at necking is \(\epsilon_{e, neck} = 0.221\).
Ejercicio\(\PageIndex{7}\)
Utilizar una construcción Considerar (parcela\(\sigma_t\) vs.\(\lambda\), como en la Figura 10) para verificar el resultado del problema anterior.
Ejercicio\(\PageIndex{8}\)
Los elastómeros (caucho) tienen relaciones esfuerzo-deformación de la forma
\[\sigma_e = \dfrac{E}{3} \left (\lambda - \dfrac{1}{\lambda^2} \right ),\nonumber\]
donde\(E\) está el módulo inicial. Usa la construcción consid`ere para mostrar si este material va a formar un cuello o dibujar.
Ejercicio\(\PageIndex{9}\)
Mostrar que un material de ley de potencia (uno que obedece a la Ecuación 1.4.8) se cuela cuando la deformación verdadera\(\epsilon_t\) se vuelve igual al exponente de endurecimiento por deformación\(n\).
Ejercicio\(\PageIndex{10}\)
Demostrar que el UTS (esfuerzo de ingeniería en el cuello incipiente) para un material de ley de potencia (Ecuación 1.4.8) es
\[\sigma_f = \dfrac{An^n}{e^n}\nonumber\]
Ejercicio\(\PageIndex{11}\)
Demostrar que la energía de deformación se\(U = \int \sigma \ d \epsilon\) puede calcular usando ingeniería o valores verdaderos de tensión y deformación, con igual resultado.
Ejercicio\(\PageIndex{12}\)
Demostrar que la energía de deformación necesaria para el cuello de un material de ley de potencia (Ecuación 1.4.8) es
\[U = \dfrac{An^{n + 1}}{n + 1}\nonumber\]


