2.1: Trusses
- Page ID
- 83349
Introducción
Un truss es un conjunto de elementos estructurales largos y esbeltos que están conectados en sus extremos. Los trusses encuentran un uso sustancial en la construcción moderna, por ejemplo como torres (ver Figura 1), puentes, andamios, etc. Además de su importancia práctica como estructuras útiles, los elementos de celosía tienen una simplicidad dimensional que nos ayudará a ampliar aún más los conceptos de mecánica introducidos en los módulos lidiar con la respuesta uniaxial. Este módulo también utilizará cerchas para introducir conceptos importantes en el análisis estático y numérico que se extenderán en módulos posteriores a problemas más generales.
Ejemplo\(\PageIndex{1}\)
Las armaduras a menudo se usan para endurecer estructuras, y la mayoría de la gente está familiarizada con los sistemas a menudo muy elaborados de arriostramiento transversal utilizados en puentes. Los arriostramientos de celosía utilizados para endurecer las torres de los puentes colgantes contra el pandeo son difíciles de perder, pero no todos notan los paneles verticales de celosía en la mayoría de esos puentes que sirven para endurecer la cubierta contra la deformación por flexión y torsión.
Muchos lectores habrán visto la muy famosa película, tomada el 7 de noviembre de 1940, de Barney Elliott de The Camera Shop en Tacoma, Washington. El viento se rachaó hasta 42 mph ese día, e indujo una secuencia de ondulaciones espectaculares y eventual colapso del puente Tacoma Narrows (Un videodisco instructivo interactivo del colapso del Puente Tacoma Narrows está disponible en Wiley Educational Software (ISBN 0-471-87320-9).). Este puente fue construido utilizando vigas en I relativamente cortas para rigidizar la cubierta en lugar de paneles de celosía, según se informa por razones estéticas; los diseños de puentes de la época favorecían estructuras cada vez más esbeltas y de apariencia elegante. Incluso durante la construcción, el puente se hizo conocido por su alarmante tendencia a balancearse en el viento, ganándose el apodo local “Gertie galopante”.
Los refuerzos de celosía se utilizaron cuando el puente fue reconstruido en 1950, y el nuevo puente estaba libre de las oscilaciones que llevaron al colapso de su predecesor. Este es un buen ejemplo de un uso importante de las cerchas, pero probablemente sea un ejemplo aún mejor del valor de la precaución y la humildad en la ingeniería. Las respuestas glib que a menudo se dan para el colapso original —ráfagas de viento resonantes, vórtices de von Karman, etc.— no son realmente satisfactorias más allá de la obvia afirmación de que la cubierta no era lo suficientemente rígida. Incluso hoy en día, ingenieros conocedores discuten sobre la complicada dinámica estructural involucrada. En última instancia, existen muchas incertidumbres incluso en diseños completados utilizando técnicas muy modernas y elaboradas. Un diseñador sabio nunca confiará plenamente en un resultado teórico, generado por computadora o no, y aprovechará la experiencia y la intuición tanto como sea posible.
Análisis estático de fuerzas
Newton observó que una masa se acelera de acuerdo con el vector suma de fuerzas aplicadas a la misma:\(\sum F = ma\). (Cantidades vectoriales indicadas por el tipo de negritas.) En las estructuras que están ancladas para evitar el movimiento, obviamente no hay aceleración y las fuerzas deben sumar a cero. Esta ecuación vectorial tiene tantos componentes escalares como la dimensionalidad del problema; para casos bidimensionales tenemos:
\[\sum F_x = 0\]
\[\sum F_y = 0\]
donde\(F_x\) y\(F_y\) son los componentes de\(F\) en las direcciones de coordenadas\(x\) y\(y\) cartesianas. Estas dos ecuaciones, que podemos interpretar como una restricción de la estructura contra el movimiento traslacional en las\(y\) direcciones\(x\) y, nos permiten resolver a lo sumo dos fuerzas desconocidas en problemas estructurales. Si la estructura está restringida tanto a la rotación como a la traslación, podemos agregar una ecuación de momento que establezca que la suma de momentos o pares en el\(x-y\) plano también debe sumar a cero:
\[\sum M_{xy} = 0\]
En dos dimensiones, entonces, tenemos tres ecuaciones de equilibrio estático que pueden ser utilizadas para resolver fuerzas desconocidas. En tres dimensiones, se suman una tercera ecuación de fuerza y dos ecuaciones de momento más, para un total de seis:
\[\begin{array} {c} {\sum F_x = 0 \ \ \ \ \ \ \sum M_{xy} = 0} \\ {\sum F_y = 0 \ \ \ \ \ \ \sum M_{xz} = 0} \\ {\sum F_z = 0 \ \ \ \ \ \ \sum M_{yz} = 0} \end{array}\]
Estas ecuaciones se pueden aplicar a la estructura como un todo, o podemos (conceptualmente) eliminar una pieza de la estructura y considerar las fuerzas que actúan sobre la pieza eliminada. Un boceto de la pieza, que muestra todas las fuerzas que actúan sobre ella, se llama diagrama de cuerpo libre. Si el número de fuerzas desconocidas en el diagrama es igual o menor que el número de ecuaciones de equilibrio estático disponibles, las incógnitas pueden resolverse de manera directa; tales problemas se denominan estáticamente determinados. Tenga en cuenta que estas ecuaciones de equilibrio no asumen nada sobre el material del que está hecha la estructura, por lo que las fuerzas resultantes también son independientes del material.
En los análisis a considerar aquí, se supone que los elementos de celosía están unidos entre sí por pasadores u otras conexiones similares que permiten una rotación libre alrededor de la junta. Como se ve en el diagrama de cuerpo libre de la Figura 2, esta incapacidad para resistir la rotación implica que la fuerza que actúa sobre la junta de pasador de un elemento de celosía debe estar en la dirección axial del elemento: cualquier componente transversal tendería a causar rotación, y si el elemento va a estar en equilibrio estático la ecuación de momento fuerza el componente transversal para desvanecerse. Si los extremos del elemento se soldaran o empernaran en lugar de simplemente anclarse, la conexión final podría transmitir fuerzas transversales y momentos de flexión al elemento. Dicha estructura se llamaría entonces marco en lugar de truss, y su análisis tendría que incluir efectos de flexión. Dichas estructuras serán tratadas en el Módulo de Doblado.
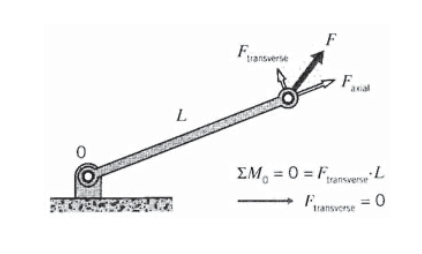
Saber que la fuerza en cada elemento de celosía debe estar en la dirección axial del elemento es la clave para resolver las fuerzas del elemento en trusses que contienen muchos elementos. Cada elemento que se encuentra en una junta de pasador tirará o empujará sobre el pasador dependiendo de si el elemento está en tensión o compresión, y dado que el pasador debe estar en equilibrio estático, la suma de todas las fuerzas del elemento que actúan sobre el pasador debe ser igual a la fuerza que se aplica externamente al pasador:
\[\sum_{e} F_i^e = F_i \nonumber\]
Aquí el\(e\) superíndice indica la fuerza vectorial suministrada por el elemento sobre el\(i^{th}\) pasador en el truss y\(F_i\) en la fuerza aplicada externamente a ese pasador. La suma es sobre todos los elementos conectados al pin.
Ejemplo\(\PageIndex{2}\)
De esta manera se puede analizar el braguero muy simple de dos elementos que a menudo se encuentra en los libros de física de secundaria y se muestra en la Figura 3. La intuición nos dice que el elemento superior, conectando las articulaciones\(A\) y\(B\), está en tensión mientras que el elemento\(BC\) está en compresión. En problemas más complicados no siempre es posible determinar el signo de la fuerza del elemento por inspección, pero no importa. Al bosquejar los diagramas de cuerpo libre para los pines, la carga se puede dibujar en cualquier dirección; si la conjetura resulta ser incorrecta, la solución dará un valor negativo para la magnitud de la fuerza.
Las fuerzas desconocidas en el pasador de conexión\(B\) están en la dirección de los elementos unidos a él, y como solo hay dos de tales fuerzas, pueden determinarse a partir de las dos ecuaciones de fuerza de equilibrio estático:
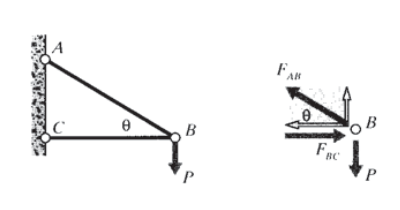
\[\sum F_y = 0 = + F_{AB} \sin \theta - P \Rightarrow F_{AB} = \dfrac{P}{\sin \theta}\nonumber\]
\[\sum F_x = 0 = -F_{AB} \cos \theta + F_{BC} \Rightarrow F_{BC} = F_{AB} \cos \theta = \dfrac{P}{\tan \theta}\nonumber\]
En armaduras más complicadas, el enfoque general es comenzar en una junta de pasador que contenga no más de dos elementos que tengan fuerzas desconocidas, y luego trabajar de junta en junta utilizando las fuerzas del elemento del paso anterior para reducir el número de incógnitas. Considere el truss de 6 elementos que se muestra en la Figura 4, en el que las juntas y los elementos se numeran como se indica, con los números de elementos apareciendo en círculos. La articulación 3 es un punto de partida natural, ya que sólo las fuerzas\(F_2\) y\(F_5\) aparecen como incógnitas. Una vez que se encuentra F5, un análisis de articulación 5 solo tiene fuerzas\(F_4\) y\(F_6\) como incógnitas. Por último, se puede completar el diagrama de cuerpo libre del nodo 2, ya que solo\(F_1\) y ahora\(F_3\) se desconocen. Entonces se completa el análisis de fuerza.
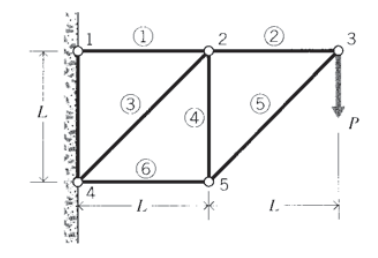
A menudo hay muchas formas de completar problemas como este, quizás siendo algunos más fáciles que otros. Otro enfoque podría ser comenzar en una de las juntas en la pared; es decir, la junta 1 o la junta 4. El problema como se indicó originalmente da a estas juntas como que tienen desplazamientos fijos en lugar de fuerzas especificadas. Este es un ejemplo de un problema de valor de límite mixto, con algunas partes del límite que tienen fuerzas especificadas y las partes restantes tienen desplazamientos especificados. Tales problemas son generalmente más difíciles, y requieren más información matemática para su solución que los problemas que tienen solo uno u otro tipo de condición límite. Sin embargo, en los problemas estáticamente determinados, la estructura se puede convertir a un tipo de solo carga invocando el equilibrio estático en la estructura como un todo. Las condiciones de límite de desplazamiento fijo se reemplazan entonces por fuerzas de reacción que se establecen en los puntos de restricción.
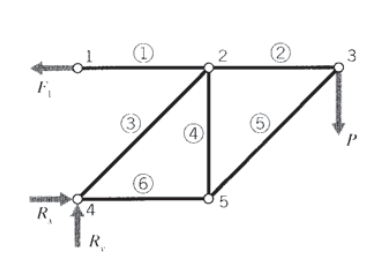
Las ecuaciones de equilibrio de momento no fueron útiles en el análisis conjunto por conjunto descrito anteriormente, ya que los elementos individuales no pueden soportar momentos. Pero como se ve en la Figura 5, podemos considerar el truss de 6 elementos como un todo y tomar momentos alrededor de la articulación 4. Con momentos que tienden en sentido contrario a las agujas del reloj son positivos, esto da
\[\sum M_4 = 0 = F_1 \times L - P \times 2 L \Rightarrow F_1 = 2P\nonumber\]
La fuerza\(F_1\) es la fuerza aplicada por la pared a la junta 1, y esto es obviamente igual a la fuerza de tracción en el elemento 1. No puede haber componente vertical de esta fuerza de reacción, ya que las fuerzas del elemento deben ser axiales y solo el elemento 1 está conectado a la junta 1. En la articulación 4, las fuerzas de reacción Rx y Ry pueden actuar tanto en la\(x\)\(y\) dirección como ya que el elemento 3 no es perpendicular a la pared. Estas fuerzas de reacción se pueden encontrar invocando el equilibrio horizontal y vertical:
\[\sum F_x = 0 = -F_1 + R_x \Rightarrow R_x = F_1 = 2P\nonumber\]
\[\sum F_y = 0 = + R_y - P \Rightarrow R_y = P\nonumber\]
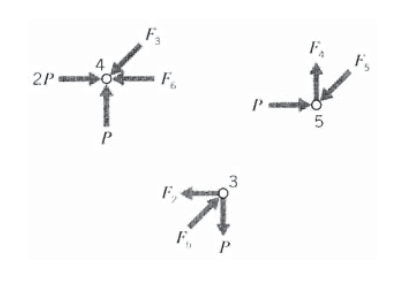
Ahora se puede iniciar un análisis conjunto por articulación a partir de la articulación 4, ya que allí solo actúan dos fuerzas desconocidas (ver Figura 6). Para el equilibrio vertical,\(F_3 \cos 45 = P\), entonces\(F_3 = \sqrt{2} P\). Entonces para el equilibrio horizontal\(F_6 + F_3 \cos 45 = 2P\), entonces\(F_6 = P\). Ahora moviéndose a la articulación 5, el equilibrio horizontal da\(F_5 \cos 45 = P\) así\(F_5 = F_3 = \sqrt{2} P\), y el equilibrio vertical\(F_4 = F_5 \cos 45\) lo da\(F_4 = P\). Por último, en la articulación 3 el equilibrio horizontal\(F_2 = F_5 \cos 45\) lo da\(F_2 = P\).
En el diseño de truss real, una vez que se conoce la fuerza de cada elemento, su área de sección transversal se puede calcular para mantener la tensión del elemento de\(\sigma = P/A\) manera segura menor que el punto de elasticidad del material. Los elementos en compresión, sin embargo, también deben analizarse para su pandeo, ya que sus relaciones de\(EI\) a\(L^2\) son generalmente bajas. La carga de pandeo se puede aumentar sustancialmente al arriostrar el elemento contra la deflexión lateral, y este arriostramiento es evidente en la mayoría de puentes y grúas. Además, los elementos de celosía generalmente se mantienen unidos por uniones soldadas o atornilladas en lugar de pasadores. Estas juntas pueden llevar algunos momentos de flexión, lo que ayuda a endurecer la armadura contra el pandeo.
Deflexiones
Puede ser importante en algunas aplicaciones que la armadura sea lo suficientemente rígida como para mantener las deformaciones dentro de límites especificados. Los telescopios astronómicos son un ejemplo, ya que la desviación de la estructura que soporta los conjuntos ópticos puede degradar la capacidad de enfoque del instrumento. Sin embargo, es probable que una torre de perforación o puente típico sea más probable que sea la resistencia que la rigidez crítica, por lo que podría parecer que las deflexiones serían relativamente poco importantes. No obstante, se verá que la consideración de las deflexiones es necesaria para resolver el gran número de estructuras que no están estáticamente determinadas. Las siguientes secciones tratan las deflexiones de truss por ambas razones.
Aproximación geométrica
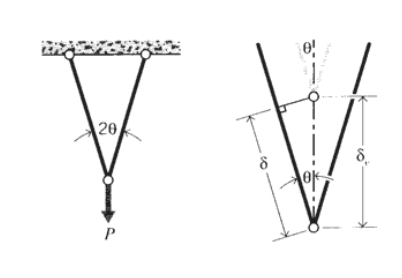
Una vez que se conoce la fuerza axial en cada elemento de celosía, las deformaciones individuales del elemento siguen directamente usando\(\delta = PL/AE\). La deflexión de cualquier punto de la celosía se puede determinar geométricamente, invocando el requisito de que los elementos permanezcan anclados juntos en sus puntos de unión. En el truss simétrico de dos elementos que se muestra en la Figura 7, la junta obviamente\(B\) se desviará verticalmente hacia abajo. La relación entre la deformación axial\(\delta\) de los elementos y la deflexión vertical de la junta\(\delta_v\) se ve entonces como
\[\delta_v = \dfrac{\delta}{\cos \theta}\nonumber\]
Aquí se supone que la deformación es lo suficientemente pequeña como para que los aspectos brutos de la geometría se mantengan esencialmente inalterados; en este caso, que el ángulo\(\theta\) es el mismo antes y después de aplicar la carga.
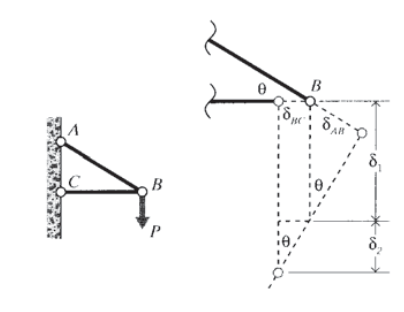
En los análisis geométricos de armaduras más complicadas, a veces es conveniente visualizar desanclar los elementos en una junta seleccionada, dejando que los elementos se alarguen o encojan de acuerdo con la fuerza axial que están transmitiendo, y luego balanceándolos alrededor de la junta aún anclada hasta que las ubicaciones de los pasadores coincidan otra vez. El movimiento de los extremos no anclados trazaría trayectorias circulares, pero si las deflexiones son pequeñas, la trayectoria se puede aproximar como una línea recta perpendicular al eje del elemento. La posición de la articulación se puede calcular a partir de las relaciones pitagóricas.
En el anterior truss de dos elementos que se muestra en la Figura 3, tuvimos\(P_{AB} = P/ \sin \theta\) y\(P_{BC} = P/ \tan \theta\). Si se\(B\) quitara el pasador en la junta, las deflexiones del elemento serían
\[\delta_{AB} = \dfrac{P}{\sin \theta} \left ( \dfrac{L}{AE} \right )_{AB} \text{ (tension)}\nonumber\]
\[\delta_{BC} = \dfrac{P}{\tan \theta} \left ( \dfrac{L}{AE} \right )_{BC} \text{ (compression)}\nonumber\]
La deflexión total hacia abajo de la articulación\(B\) es entonces
\[\delta_v = \delta_1 + \delta_2= \dfrac{\delta_{AB}}{\sin \theta} + \dfrac{\delta_{BC}}{\tan \theta}\nonumber\]
\[= \dfrac{P}{\sin^2 \theta} \left ( \dfrac{L}{AE} \right )_{AB} + \dfrac{P}{\tan^2 \theta} \left ( \dfrac{L}{AE} \right )_{BC} \nonumber\]
Estas deflexiones se muestran en la Figura 8.
La deflexión horizontal\(\delta_h\) del pasador es más fácil de calcular, ya que es solo la contracción del elemento\(BC\):
\[\delta_h = \delta_{BC} = \dfrac{P}{\tan \theta} \left ( \dfrac{L}{AE} \right )_{BC} \nonumber\]
Enfoque energético
El enfoque geométrico para el análisis de deformación de celosía puede ser bastante tedioso, especialmente a medida que los problemas se agrandan. Muchos problemas se pueden resolver más fácilmente usando una energía de tensión en lugar de un enfoque de fuerza en un punto. La energía de deformación total\(U\) en un solo elemento de celosía cargado elásticamente es
\[U = \int P\ d\delta\nonumber\]
El incremento de deformación\(d\delta\) está relacionado con un incremento correspondiente de carga\(dP\) por
\[\delta = \dfrac{PL}{AE} \Rightarrow d\delta = \dfrac{L}{AE} dP\nonumber\]
La energía de deformación es entonces
\[U = \int P \dfrac{L}{AE} dP = \dfrac{P^2L}{2AE}\nonumber\]
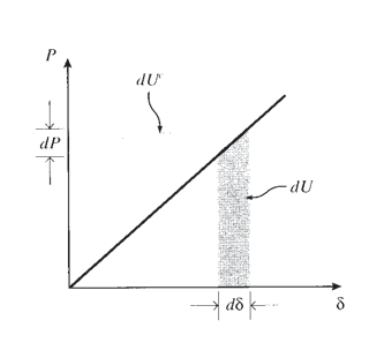
El incremento incremental en la energía de deformación correspondiente a un incremento en la deformación\(d\delta\) es justo\(dU = P d\delta\). Si la curva fuerza-alargamiento es lineal, esto es idéntico al aumento en la cantidad llamada energía de deformación complementaria:\(dU^c = \delta dP\). Estas cantidades se representan en la Figura 9. Ahora considere un sistema con muchas juntas, sometido a una serie de cargas que actúan en diferentes juntas. Si aumentáramos ligeramente la\(i^{th}\) carga manteniendo constantes todas las demás cargas, el incremento en la energía complementaria total del sistema sería
\[dU^c = \delta_i dP_i\nonumber\]
donde\(\delta_i\) está el desplazamiento que se produciría en la ubicación de\(P_i\), moviéndose en la misma dirección que el vector de fuerza para\(P_i\). Reorganizar,
\[\delta_i = \dfrac{\partial U^c}{\partial P_i}\nonumber\]
y desde\(U^c = U\):
\[\delta_i = \dfrac{\partial U}{\partial P_i}\]
De ahí que el desplazamiento en un punto dado sea la derivada de la energía de deformación total con respecto a la carga que actúa en ese punto. Esto proporciona la base de un método extremadamente útil de análisis de desplazamiento conocido como Teorema de Castigliano (De la tesis de 1873 del ingeniero italiano Alberto Castigliano (1847—1884), en el Instituto Politécnico de Turín.), que puede afirmarse para problemas de truss como la siguiente receta:
- Que la carga aplicada en la articulación cuya deformación se busca, en la dirección de la deformación deseada, se escriba como una variable algebraica, digamos\(Q\). Si la carga es conocida numéricamente, reemplace el número por una letra. Si no hay carga en la ubicación y dirección deseadas, pon ahí una imaginaria que se pondrá a cero al final del problema.
- Resuelve las fuerzas\(F_i(Q)\) en cada elemento de celosía, cada una de las cuales puede depender de la carga\(Q\) asignada en el paso anterior.
- Use estas fuerzas para calcular la energía de deformación para cada elemento, y sume las energías en cada elemento para obtener la energía de deformación total para la armadura:
\[U_{tot} = \sum_{i} U_i = \sum_i \dfrac{F_i^2 L_i}{2A_i E_i}\]
Cada término en esta suma puede contener la variable\(Q\). - La deformación congruente con\(Q\), es decir, la deformación en el punto donde\(Q\) se aplica y en la misma dirección que\(Q\), es entonces
\[\delta_Q = \dfrac{\partial U_{tot}}{\partial Q} = \sum_i \dfrac{F_i L_i}{A_i E_i} \dfrac{\partial F_i (Q)}{\partial Q}\] - La carga\(Q\) es reemplazada por su valor numérico, si se conoce. O por cero, si se trataba de una carga imaginaria en primer lugar.
Aplicando este método a la deflexión vertical del truss de dos elementos de la Figura 3, el problema ya tiene una fuerza en la dirección requerida, la carga aplicada hacia abajo\(P\). Ya se ha demostrado que las fuerzas son\(P_{AB} = P/ \sin \theta\) y\(P_{BC} = P/ \tan \theta\), por lo que la deflexión vertical puede escribirse inmediatamente como
\[\begin{align*} \delta_v &= P_{AB} \left ( \dfrac{L}{AE} \right )_{AB} \dfrac{\partial P_{AB}}{\partial P} + P_{BC} \left ( \dfrac{L}{AE} \right )_{BC} \dfrac{\partial P_{BC}}{\partial P} \\[4pt] &=\dfrac{P}{\sin \theta} \left ( \dfrac{L}{AE} \right )_{AB} \dfrac{1}{\sin \theta} + \dfrac{P}{\tan \theta} \left ( \dfrac{L}{AE} \right )_{AB} \dfrac{1}{\sin \theta} + \dfrac{P}{\tan \theta} \left ( \dfrac{AE}{L} \right )_{BC} \dfrac{1}{\tan \theta} \end{align*}\]
Esto es idéntico a la expresión obtenida a partir de consideraciones geométricas. El método energético no ahorró demasiados pasos algebraicos en este caso, sino que evitó tener que visualizar e idealizar los desplazamientos geométricamente.
Si\(B\) se desea el desplazamiento horizontal en la articulación, el método requiere que exista una fuerza horizontal en ese punto. No se da uno, así que ahí colocamos uno imaginario, digamos\(Q\). El truss se vuelve a analizar estáticamente para encontrar cómo las fuerzas del elemento son influenciadas por esta nueva fuerza\(Q\). La fuerza del elemento superior es\(P_{AB} = P/\sin \theta\) como antes, y la fuerza del elemento inferior se vuelve\(P_{BC} = P/ \tan \theta - Q\). Repitiendo el proceso Castigliano, pero ahora diferenciando con respecto a\(Q\)
\[\delta_h = P_{AB} \left ( \dfrac{L}{AE} \right )_{AB} \dfrac{\partial P_{AB}}{\partial P} + P_{BC} \left ( \dfrac{L}{AE} \right )_{BC} \dfrac{\partial P_{BC}}{\partial P}\nonumber\]
\[= \dfrac{P}{\sin \theta} \left ( \dfrac{L}{AE} \right )_{AB} \cdot 0 + \left (\dfrac{P}{\tan \theta} - Q \right ) \left ( \dfrac{L}{AE} \right )_{BC} (-1)\nonumber\]
El primer término desaparece tras la diferenciación ya que\(Q\) no apareció en la expresión para\(P_{AB}\). Esta es la forma del método de notar que la deflexión horizontal está determinada completamente por la contracción del elemento\(BC\). Al establecer\(Q = O\), el resultado final es
\[\delta_h = -\dfrac{P}{\tan \theta} \left ( \dfrac{AE}{L} \right )_{BC}\nonumber\]
como antes.
Ejemplo\(\PageIndex{3}\)
Considere el truss de 6 elementos de la Figura 4 cuyas fuerzas de elementos individuales se encontraron anteriormente mediante diagramas de cuerpo libre. Buscamos la desviación vertical del nodo 3, que es congruente con la fuerza\(P\). Usando el método de Castigliano, esta deflexión es la derivada de la energía de deformación total con respecto a\(P\). Equivalentemente, podemos diferenciar la energía de deformación de cada elemento con respecto a\(P\) individualmente, y luego sumar las contribuciones de cada elemento para obtener el resultado final:
\[\delta_P = \dfrac{\partial}{\partial P} \sum_i \dfrac{F_i^2L_i}{2A_i E_i} = \sum_i \left (\dfrac{F_i L_i}{A_i E_i} \dfrac{\partial F_i}{\partial P} \right )\nonumber\]
Para sistematizar este enfoque, podemos formar una tabla de parámetros necesarios de la siguiente manera:
| \(i\) | \(F_i\) | \(\dfrac{L_i}{A_iE_i}\) | \(\dfrac{\partial F_i}{\partial P\) | \(\dfrac{F_i L_i}{A_i E_i} \dfrac{\partial F_i}{\partial P}\) |
| 1 | \(2P\) | \(L/AE\) | 2 | \(4PL/AE\) |
| 2 | \(P\) | \(L/AE\) | 1 | \(PL/AE\) |
| 3 | \(\sqrt{2} P\) | \(\sqrt{2} L/AE\) | \(\sqrt{2}\) | \(2.83 PL/AE\) |
| 4 | \(P\) | \(L/AE\) | 1 | \(PL/AE\) |
| 5 | \(\sqrt{2} P\) | \(\sqrt{2} L/AE\) | \(\sqrt{2}\) | \(2.83 PL/AE\) |
| 6 | \(P\) | \(L/AE\) | 1 | \(PL/AE\) |
Si por ejemplo tenemos como parámetros numéricos\(P = 1000\ lbs\),\(L = 100\ in\),\(E = 30\ Mpsi\) y\(A = 0.5\ in^2\), entonces\(\delta_P = 0.0844\ in\).
Trusses estáticamente indeterminados
Ya se ha señalado que las fuerzas elementales en los problemas de truss tratados hasta ahora no dependen de las propiedades de los materiales utilizados en su construcción, así como la tensión en una simple prueba de tensión es independiente del material. Este resultado, que sin duda hace que el problema sea más fácil de resolver, es consecuencia de que los problemas anteriores se determinan estáticamente; es decir, se pueden resolver utilizando únicamente las ecuaciones de equilibrio estático. La determinación estática, entonces, es un aspecto importante de la dificultad que podemos esperar para resolver el problema. No todos los problemas son estáticamente determinados, y una consecuencia de esta indeterminación es que las fuerzas en la estructura pueden depender de las propiedades del material.
Después de realizar un análisis estático de la armadura como un todo para encontrar fuerzas de reacción en los soportes, típicamente tratamos de encontrar las fuerzas de los elementos utilizando el método de articulación a la vez descrito anteriormente. Sin embargo, puede haber como máximo dos fuerzas desconocidas en una junta de pasador en un problema de truss bidimensional si la junta se va a resolver usando solo la estática, ya que la ecuación de momento no proporciona información utilizable en este caso. Si hay más incógnitas sin importar en qué orden se analicen las uniones de celosía, entonces se debe encontrar una serie de ecuaciones adicionales iguales a las incógnitas restantes. Estas ecuaciones adicionales son aquellas que hacen cumplir la compatibilidad de los diversos desplazamientos de las articulaciones, cada uno de los cuales debe ser tal que mantenga las uniones de celosía ancladas entre sí.
Ejemplo\(\PageIndex{4}\)
Un ejemplo sencillo, solo dos elementos de celosía actuando en paralelo como se muestra en la Figura 10, mostrará el enfoque necesario. Aquí la condición de compatibilidad es solo
\[\delta_A = \delta_B\nonumber\]
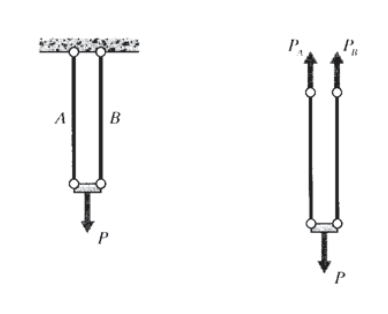
Los desplazamientos de elementos individuales están relacionados con las fuerzas del elemento por\(\delta = PL/AE\), que depende del material y se puede denominar una ecuación constitutiva porque refleja la constitución mecánica del material. Combinar esto con la condición de compatibilidad da
\[\dfrac{P_AL}{A_A E_A} = \dfrac{P_BL}{A_BE_B} \Rightarrow P_B = P_A \dfrac{A_BE_B}{A_AE_A}\nonumber\]
Finalmente, las fuerzas individuales de los elementos deben sumar a la carga\(P\) total aplicada para satisfacer el equilibrio:
\[P = P_A + P_B = P_A + P_A \dfrac{A_BE_B}{A_A E_A} \Rightarrow P_A = P \left (\dfrac{1}{1 + (\tfrac{A_BE_B}{A_AE_A})} \right )\nonumber\]
Tenga en cuenta que la respuesta final en el ejemplo anterior depende de las dimensiones del elemento y de las rigideces del material, como se prometió. Aquí la condición de compatibilidad geométrica era muy simple y obvia, es decir, que los desplazamientos de las juntas de extremo de dos elementos eran idénticos. En cerchas más complejas estas relaciones pueden ser sutiles, pero tienden a hacerse más evidentes con la práctica.
En el problema anterior se utilizaron tres tipos diferentes de relaciones: una ecuación de compatibilidad, que establece cómo la estructura debe deformarse cinemáticamente para permanecer conectada; una ecuación constitutiva, que encarna la respuesta tensión-deformación del material; y una ecuación de equilibrio, afirmando que las fuerzas deben suma a cero si se quiere evitar la aceleración. Estos tres conceptos, hechos matemáticamente algo más generales para manejar problemas geométricamente más elaborados, subyacen a toda la mecánica de sólidos.
En el Módulo sobre Respuesta Elástica, observamos que el esfuerzo en una muestra de tracción está determinado únicamente por consideraciones de equilibrio estático, siendo dado por\(\sigma = P/A\) independiente de las propiedades del material. Vemos ahora que la determinación estática depende, entre otras cosas, de que el material sea homogéneo, es decir, idéntico en todas partes. Si la muestra de tracción está compuesta por dos subunidades cada una con propiedades diferentes, las tensiones se asignarán de manera diferente entre las dos unidades, y las tensiones no serán uniformes. Siempre que una fórmula de tensión o deformación se copie de un manual, el usuario debe tener cuidado de anotar las limitaciones de la teoría subyacente. Las fórmulas del manual suelen ser aplicables solo a materiales homogéneos en su rango elástico lineal, y se deben usar teorías de orden superior cuando no se cumplen estas condiciones.
Ejemplo\(\PageIndex{5}\)
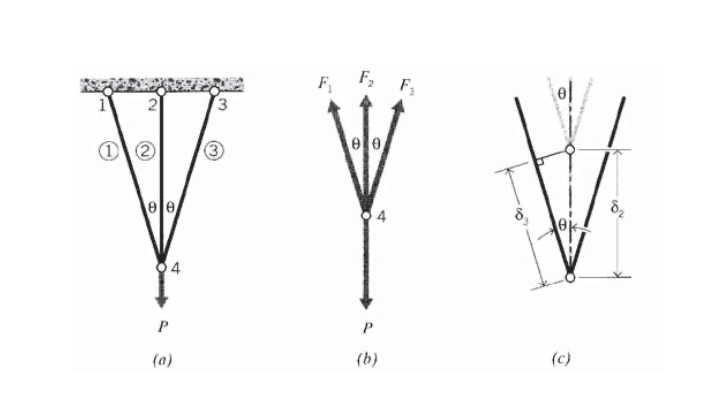
La Figura 11 (a) muestra otra celosía estáticamente indeterminada, con tres elementos que tienen la misma área y módulo 11, pero diferentes longitudes, reuniéndose en un nodo común. De un vistazo, podemos ver que el nodo 4 tiene tres elementos que se encuentran ahí cuyas fuerzas son desconocidas, y esta es una más de las útiles ecuaciones de equilibrio estático que podrán manejar. Esto también es evidente en el diagrama de cuerpo libre de la Figura 11 (b): el equilibrio horizontal y vertical da
\[\sum F_x = 0 = -F_1 + F_2 \to F_1 = F_2\nonumber\]
\[\sum F_y = 0 = -P + F_2 + F_1 \cos \theta + F_3 \cos \theta \to F_2 + 2 F_3 \cos \theta = P\]
Estas dos ecuaciones claramente no son suficientes para determinar las incógnitas\(F_1, F_2, F_3\). Necesitamos otra ecuación, y se proporciona al requerir que la deformación sea tal que mantenga la armadura anclada en el nodo 4. Dado que la simetría de los problemas nos dice que la deflexión allí es recta hacia abajo, se puede utilizar el diagrama de la Figura 11 (c). Y dado que la deflexión es pequeña en relación con las longitudes de los elementos, el ángulo del elemento 3 permanece esencialmente sin cambios después de la deformación. Esto nos permite escribir
\[\delta_3 = \delta_2 \cos \theta\nonumber\]
o
\[\dfrac{F_3L_3}{A_3E_3} = \dfrac{F_2L_2}{A_2E_2} \cos \theta \nonumber\]
Usar\(A_2 = A_3\),\(E_2 = E_3\),\(L_3 = L\), y\(L_2 = L \cos \theta\), esto se convierte
\[F_3 = F_2 \cos^2 \theta\nonumber\]
Resolviendo esto simultáneamente con la Ecuación 2.1.8, obtenemos
\[F_2 = \dfrac{P}{1 + 2 \cos^3 \theta}, F_3 = \dfrac{P \cos^2 \theta}{1 + 2 \cos^3 \theta}\nonumber\]
Obsérvese que el módulo\(E\) no aparece en este resultado, aunque el problema es estáticamente indeterminado. Si los elementos tuvieran diferentes rigideces, sin embargo, la cancelación de no\(E\) habría ocurrido.
Análisis matricial de cerchas
El análisis de cuerpo libre conjunto por articulación de armaduras es tedioso para estructuras grandes y complicadas, especialmente si la indeterminación estática requiere que se considere la compatibilidad de desplazamiento junto con el equilibrio estático. Sin embargo, incluso las cerchas estáticamente indeterminadas pueden resolverse de manera rápida y confiable tanto para las fuerzas como para los desplazamientos mediante un procedimiento numérico sencillo conocido como análisis estructural matricial. Este método es un precursor del método informático más general denominado análisis de elementos finitos (FEA), que ha llegado a dominar gran parte del análisis de ingeniería en las últimas dos décadas. Aquí se describirán los fundamentos del análisis matricial, principalmente como una introducción al uso más general de FEA en el análisis de estrés.
El análisis matricial de las cerchas opera considerando la rigidez de cada elemento de celosía uno a la vez, y luego usando estas rigideces para determinar las fuerzas que se configuran en los elementos de celosía por los desplazamientos de las juntas, generalmente llamadas “nodos” en el análisis de elementos finitos. Después al señalar que la suma de las fuerzas aportadas por cada elemento a un nodo debe ser igual a la fuerza que se aplica externamente a ese nodo, podemos ensamblar una secuencia de ecuaciones algebraicas lineales en las que los desplazamientos nodales son las incógnitas y las fuerzas nodales aplicadas son cantidades conocidas. Estas ecuaciones están convenientemente escritas en forma de matriz, lo que le da nombre al método:
\[\begin{bmatrix} K_{11} & K_{12} & \cdots & K_{1n} \\ K_{21} & K_{22} & \cdots & K_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ K_{n1} & K_{n2} & \cdots & K_{nn} \end{bmatrix} \left \{ \begin{matrix} u_1 \\ u_2 \\ \cdots \\ u_n \end{matrix} \right \} = \left \{ \begin{matrix} f_1 \\ f_2 \\ \cdots \\ f_n \end{matrix} \right \}\nonumber\]
Aquí\(u_i\) e\(f_j\) indicar la deflexión en el\(i^{th}\) nodo y la fuerza en el\(j^{th}\) nodo (estas serían en realidad cantidades vectoriales, con subcomponentes a lo largo de cada eje de coordenadas). La matriz de\(K_{ij}\) coeficientes se denomina matriz de rigidez global, siendo el\(ij\) componente físicamente la influencia del\(j^{th}\) desplazamiento sobre la\(i^{th}\) fuerza. Las ecuaciones matriciales se pueden abreviar como
\[K_{ij} u_j = f_i \text{ or } Ku = f\]
usando subíndices o negritas para indicar cantidades de vectores y matrices.
Ya sea la fuerza aplicada externamente o el desplazamiento se conoce al principio para cada nodo, y es imposible especificar simultáneamente tanto un desplazamiento arbitrario como una fuerza sobre un nodo dado. Estas fuerzas nodales prescritas y desplazamientos son las condiciones límite del problema. Es tarea de análisis determinar las fuerzas que acompañan a los desplazamientos impuestos, y los desplazamientos en los nodos donde se aplican fuerzas externas conocidas.
Matriz de rigidez para un solo elemento de celosía
Como primer paso en el desarrollo de un conjunto de ecuaciones matriciales que describan los sistemas de celosía, necesitamos una relación entre las fuerzas y los desplazamientos en cada extremo de un solo elemento de celosía. Considera tal elemento en el\(x-y\) plano como se muestra en la Figura 12, unido a nodos numerados\(i\)\(j\) e inclinados en ángulo con respecto\(\theta\) a la horizontal.
Considerando el vector de elongación\(\delta\) a resolver en direcciones a lo largo y transversal al elemento, el alargamiento en el elemento de celosía puede escribirse en términos de las diferencias en los desplazamientos de sus puntos finales:
\[\delta = (u_j \cos \theta + v_j \sin \theta) - (u_i \cos \theta + v_i \sin \theta)\nonumber\]
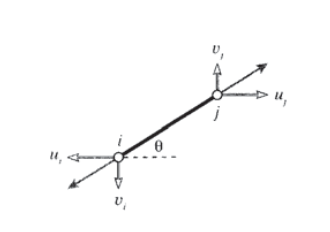
donde\(u\) y\(v\) son los componentes horizontal y vertical de las deflexiones, respectivamente. (Los desplazamientos en el nodo\(i\) dibujado en la Figura 12 son negativos.) Esta relación se puede escribir en forma de matriz como:
\[\delta = \begin{bmatrix} -c & -s & c & s \end{bmatrix} \left \{ \begin{matrix} u_i \\ v_i \\ u_j \\ v_j \end{matrix} \right \}\nonumber\]
Aquí\(c = \cos \theta\) y\(s = \sin \theta\).
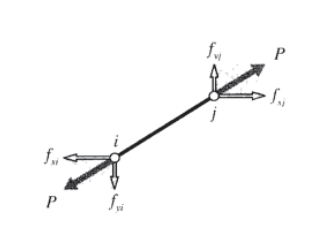
La fuerza axial P que acompaña al alargamiento\(\delta\) viene dada por la ley de Hooke para cuerpos elásticos lineales como\(P = (AE/L)\delta\). Las fuerzas nodales horizontales y verticales se muestran en la Figura 13; estas pueden escribirse en términos de la fuerza axial total como:
\[\left \{ \begin{matrix} f_{xi} \\ f_{yi} \\ f_{xj} \\ f_{yj} \end{matrix} \right \} = \left \{ \begin{matrix} -c \\ -s \\ c \\ s \end{matrix} \right \} P = \left \{ \begin{matrix} -c \\ -s \\ c \\ s \end{matrix} \right \} \dfrac{AE}{L} \delta\nonumber\]
\[\left \{ \begin{matrix} -c \\ -s \\ c \\ s \end{matrix} \right \} \dfrac{AE}{L} \begin{bmatrix} -c & -s & c & s \end{bmatrix} \left \{ \begin{matrix} u_i \\ v_i \\ u_j \\ v_j \end{matrix} \right \}\nonumber\]
Realización de la multiplicación matricial:
\[\left \{ \begin{matrix} f_{xi} \\ f_{yi} \\ f_{xj} \\ f_{yj} \end{matrix} \right \} = \dfrac{AE}{L} \begin{bmatrix} c^2 & cs & -c^2 & -cs \\ cs & s^2 & -cs & -s^2 \\ -c^2 & -cs & c^2 & cs \\ -cs & -s^2 & cs & s^2 \end{bmatrix} \left \{ \begin{matrix} u_i \\ v_i \\ u_j \\ v_j \end{matrix} \right \}\]
La cantidad entre paréntesis, multiplicada por\(AE/L\), se conoce como la “matriz de rigidez del elemento”\(k_{ij}\). Cada uno de sus términos tiene un significado físico, representando la contribución de uno de los desplazamientos a una de las fuerzas. El sistema global de ecuaciones se forma combinando las matrices de rigidez de elementos de cada elemento de celosía a su vez, por lo que su cálculo es central para el método de análisis estructural matricial. La principal diferencia entre el método de celosía matricial y el método general de elementos finitos radica en cómo se forman las matrices de rigidez de elementos; la mayoría de las otras operaciones informáticas son las mismas.
Ensamblaje de contribuciones de múltiples elementos
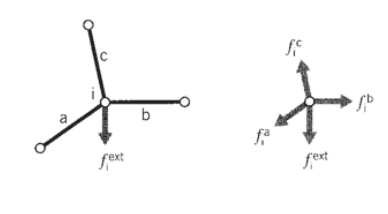
El siguiente paso es considerar un ensamblaje de muchos elementos de celosía conectados por uniones de pasador. Cada elemento que se reúne en una articulación, o nodo, aportará allí una fuerza según lo dictado por los desplazamientos de ambos nodos de ese elemento (ver Figura 14). Para mantener el equilibrio estático, todas las contribuciones de fuerza de elemento\(f_i^{elem}\) en un nodo dado deben sumarse a la fuerza\(f_i^{ext}\) que se aplica externamente en ese nodo:
\[f_i^{ext} = \sum_{elem} f_i^{elem} = (\sum_{elelm} k_{ij}^{elem} u_j) = (\sum_{elem} k_{ij}^{elem}) u_j = K_{ij} u_j\nonumber\]
Cada matriz de rigidez de elemento\(k_{ij}^{elem}\) se agrega a la ubicación apropiada de la matriz de rigidez global o “global”\(K_{ij}\) que relaciona todos los desplazamientos y fuerzas de la armadura. Este proceso se llama “montaje”. Los números de índice en la relación anterior deben ser los números “globales” asignados a la estructura de celosía en su conjunto. Sin embargo, generalmente es conveniente calcular las matrices de rigidez de elementos individuales usando un esquema local, y luego hacer que la computadora convierta a números globales al ensamblar las matrices individuales.
Ejemplo\(\PageIndex{6}\)
El proceso de ensamblaje está en el corazón del método de elementos finitos, y vale la pena hacer un simple caso a mano para ver cómo funciona realmente. Consideremos el problema del truss de dos elementos de la Figura 7, asignándose a los nodos números arbitrarios “globales” del 1 al 3. Dado que cada nodo puede moverse en general en dos direcciones, hay 3\(\times\) 2 = 6 grados totales de libertad en el problema. La matriz de rigidez global será entonces una matriz de\(\times\) 6 6 relacionando los seis desplazamientos con las seis fuerzas aplicadas externamente. Solo se desconoce uno de los desplazamientos en este caso, ya que todos menos el desplazamiento vertical del nodo 2 (grado de libertad número 4) está restringido a ser cero. La Figura 15 muestra una lista viable de los números globales, y también números “locales” para cada elemento individual.
Utilizando los números locales, la matriz de rigidez de\(\times\) 4 4 elementos de cada uno de los dos elementos puede evaluarse de acuerdo con la Ecuación 2.1.10. El ángulo de inclinación se calcula a partir de las coordenadas nodales como
\[\theta = \tan^{-1} \dfrac{y_2 -y_1}{x_2 - x_1}\nonumber\]
La matriz resultante para el elemento 1 es:
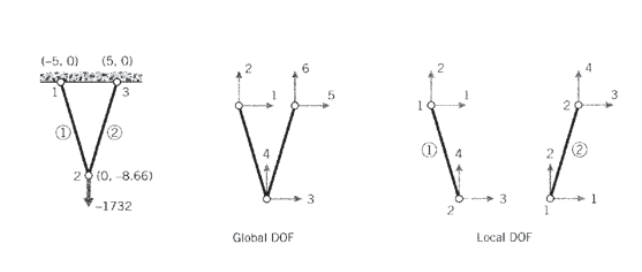
\[k^{(1)} = \begin{bmatrix} 25.00 & -43.30 & -25.00 & 43.30 \\ -43.30 & 75.00 & 43.30 & -75.00 \\ -25.00 & 43.30 & 25.00 & -43.30 \\ 43.30 & -75.00 & -43.30 & 75.00 \end{bmatrix} \times 10^3\nonumber\]
y para el elemento 2:
\[k^{(2)} = \begin{bmatrix} 25.00 & 43.30 & -25.00 & -43.30 \\ 43.30 & 75.00 & -43.30 & -75.00 \\ -25.00 & -43.30 & 25.00 & 43.30 \\ -43.30 & -75.00 & 43.30 & 75.00 \end{bmatrix} \times 10^3\nonumber\]
(Es importante que las unidades sean consistentes; aquí las longitudes están en pulgadas, las fuerzas en libras y los módulos en psi. El módulo de ambos elementos es\(E = 10\) Mpsi y ambos tienen área\(A = 0.1\ in^2\).) Estas matrices tienen filas y columnas numeradas del 1 al 4, correspondientes a los grados locales de libertad del elemento. Sin embargo, cada uno de los grados locales de libertad puede ser igualado a uno de los grados globales del problema general. Por inspección de la Figura 15, podemos formar la siguiente tabla que mapea números locales a globales:
| local | global, elemento 1 | global, elemento 2 |
| 1 | 1 | 3 |
| 2 | 2 | 4 |
| 3 | 3 | 4 |
| 4 | 4 | 6 |
Usando esta tabla, vemos por ejemplo que el segundo grado de libertad para el elemento 2 es el cuarto grado de libertad en el sistema de numeración global, y el tercer grado local de libertad corresponde al quinto grado global de libertad. De ahí que el valor en la segunda fila y tercera columna de la matriz de rigidez del elemento 2, denotado\(k_{23}^{(2)}\), debe agregarse a la posición en la cuarta fila y quinta columna de la matriz de rigidez global\(\times\) 6 6. Escribimos esto como
\[k_{23}^{(2)} \to K_{4,5}\nonumber\]
Cada una de las dieciséis posiciones en la matriz de rigidez de cada uno de los dos elementos debe agregarse a la matriz global de acuerdo con el mapeo dado por la tabla. Esto da el resultado
\[K = \begin{bmatrix} k_{11}^{(1)} & k_{12}^{(1)} & k_{13}^{(1)} & k_{14}^{(1)} & 0 & 0 \\ k_{21}^{(1)} & k_{22}^{(1)} & k_{23}^{(1)} & k_{24}^{(1)} & 0 & 0 \\ k_{31}^{(1)} & k_{32}^{(1)} & k_{33}^{(1)} + k_{11}^{(2)} & k_{34}^{(1)} + k_{12}^{(2)} & k_{13}^{(2)} & k_{14}^{(2)} \\ k_{41}^{(1)} & k_{42}^{(1)} & k_{43}^{(1)} + k_{21}^{(2)} & k_{44}^{(1)} + k_{22}^{(2)} & k_{23}^{(2)} & k_{24}^{(2)} \\ 0 & 0 & k_{31}^{(2)} & k_{32}^{(2)} & k_{33}^{(2)} & k_{34}^{(2)} \\ 0 & 0 & k_{41}^{(2)} & k_{42}^{(2)} & k_{43}^{(2)} & k_{44}^{(2)} \end{bmatrix}\nonumber\]
Esta matriz premultiplica el vector de desplazamientos nodales de acuerdo con la Ecuación 2.1.9 para producir el vector de fuerzas nodales aplicadas externamente. Las ecuaciones del sistema completo, teniendo en cuenta las fuerzas y desplazamientos conocidos, son entonces
\[10^3 \begin{bmatrix} 25.0 & -43.3 & -25.0 & 43.0 & 0.0 & 0.00 \\ -43.3 & 75.0 & 43.3 & -75.0 & 0.0 & 0.00 \\ -25.0 & 43.3 & 50.0 & 0.0 & -25.0 & -43.30 \\ 43.3 & -75.0 & 0.0 & 150.0 & -43.3 & -75.00 \\ 0.0 & 0.0 & -25.0 & -43.3 & 25.0 & 43.30 \\ 0.0 & 0.0 & -43.3 & -75.0 & 43.3 & 75.00 \end{bmatrix} \left \{ \begin{array} 0 \\ 0 \\ 0 \\ u_4 \\ 0 \\ 0 \end{array} \right \} = \left \{ \begin{array} f_1 \\ f_2 \\ f_3 \\ -1732 \\ f_5 \\ f_5 \end{array} \right \}\nonumber\]
Obsérvese que ya sea se conoce la fuerza o el desplazamiento por cada grado de libertad, siendo desconocido el desplazamiento o fuerza que lo acompaña. Aquí solo se desconoce uno de los desplazamientos (\(u_4\)), pero en la mayoría de los problemas los desplazamientos desconocidos superan con creces en número a las fuerzas desconocidas. Tenga en cuenta también que solo aquellos elementos que están físicamente conectados a un nodo dado pueden aportar una fuerza a ese nodo. En la mayoría de los casos, esto da como resultado que la matriz de rigidez global contenga muchos ceros correspondientes a pares nodales que no están abarcados por un elemento. Las implementaciones efectivas de computadoras aprovecharán la escasez de la matriz para conservar la memoria y reducir el tiempo de ejecución.
En problemas mayores las ecuaciones matriciales se resuelven para los desplazamientos y fuerzas desconocidos por reducción gaussiana u otras técnicas. En este problema de dos elementos, la solución para el único desplazamiento desconocido se puede anotar casi a partir de la inspección. Multiplicando la cuarta fila del sistema, tenemos
\[0 + 0 + 0 + 150 \times 10^3 u_4 + 0 + 0 = -1732\nonumber\]
\[u_4 = -1732/150 \times 10^3 = -0.01155 \ in\nonumber\]
Ahora cualquiera de las fuerzas desconocidas se puede obtener directamente. Multiplicar la primera fila, por ejemplo, da
\[0 + 0 + 0 + (43.4) (-0.0115) \times 10^3 + 0 + 0 = f_1\nonumber\]
\[f_1 = -500 \ lb\nonumber\]
El signo negativo aquí indica que la fuerza horizontal en el nodo global #1 está a la izquierda, opuesta a la dirección asumida en la Figura 15.
El proceso de ciclar a través de cada elemento para formar la matriz de rigidez del elemento, ensamblar la matriz de elementos en las posiciones correctas en la matriz global, resolver las ecuaciones para desplazamientos y luego retromultiplicar para calcular las fuerzas, e imprimir los resultados puede automatizarse para hacer una muy código de computadora versátil.
El análisis de elementos finitos a mayor escala (y otros) se realiza mejor con un código informático dedicado, y uno excelente para aprender el método está disponible en la web en (https://web.archive.org/web/20060108...urceforge.net/). Este código, llamado felt, fue escrito por Jason Gobat y Darren Atkinson para uso educativo, e incorpora una serie de características novedosas para promover la facilidad de uso. La información completa que describe este código, así como la fuente en lenguaje C y una serie de ejecuciones de prueba y módulo de código auxiliar está disponible a través de sus páginas web. Si tiene acceso a estaciones de trabajo X-window, también está disponible un shell gráfico llamado velvet.
Ejemplo\(\PageIndex{7}\)
Para ilustrar cómo opera este código para un problema algo mayor, considere la armadura de seis elementos de la Figura 4, analizada anteriormente tanto por el enfoque de análisis de cuerpo libre conjunto a la vez como por el método de Castigliano. El truss es redibujado en la Figura 16 por la interfaz gráfica de terciopelo.
El conjunto de datos de entrada, que puede escribirse manualmente o desarrollarse gráficamente en terciopelo, emplea técnicas de análisis para simplificar lo que puede ser un paso muy tedioso y propenso a errores en el análisis de elementos finitos. El conjunto de datos para este truss de 6 elementos es:
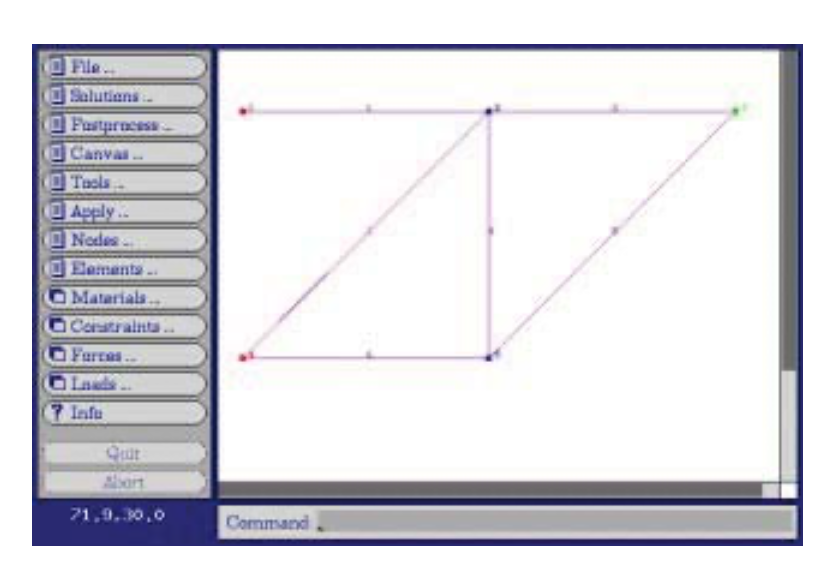
problem description nodes=5 elements=6 nodes 1 x=0 y=100 z=0 constraint=pin 2 x=100 y=100 z=0 constraint=planar 3 x=200 y=100 z=0 force=P 4 x=0 y=0 z=0 constraint=pin 5 x=100 y=0 z=0 constraint=planar truss elements 1 nodes=[1,2] material=steel 2 nodes=[2,3] 3 nodes=[4,2] 4 nodes=[2,5] 5 nodes=[5,3] 6 nodes=[4,5] material properties steel E=3e+07 A=0.5 distributed loads constraints free Tx=u Ty=u Tz=u Rx=u Ry=u Rz=u pin Tx=c Ty=c Tz=c Rx=u Ry=u Rz=u planar Tx=u Ty=u Tz=c Rx=u Ry=u Rz=u forces P Fy=-1000 end
El significado de estas líneas debe ser bastante evidente en la inspección, aunque la documentación sentida debe ser consultada para mayor detalle. La salida producida por el fieltro para estos datos es:
** ** Nodal Displacements ---------------------------------------------------------------- Node # DOF 1 DOF 2 DOF 3 DOF 4 DOF 5 DOF 6 ---------------------------------------------------------------- 1 0 0 0 0 0 0 2 0.013333 -0.03219 0 0 0 0 3 0.02 -0.084379 0 0 0 0 4 0 0 0 0 0 0 5 -0.0066667 -0.038856 0 0 0 0 Element Sress ----------------------------------------------------- 1: 4000 2: 2000 3: -2828.4 4: 2000 5: -2828.4 6: -2000 Material Usage Summary -------------------------- Material: steel Number: 6 Length: 682.8427 Mass: 0.0000 Total mass: 0.0000
Obsérvese que el desplazamiento vertical del nodo 3 (el valor DOF 2) es -0.0844, el mismo valor obtenido anteriormente en Ejemplo\(\PageIndex{3}\). La Figura 17 muestra la salida gráfica de terciopelo para las deflexiones del truss (muy ampliadas).
Ejercicio\(\PageIndex{1}\)
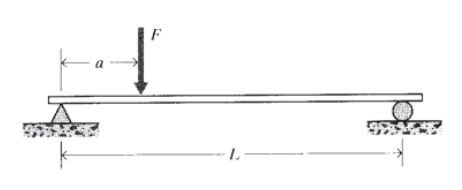
Una viga rígida de longitud\(L\) descansa sobre dos soportes que resisten el movimiento vertical, y es cargada por una fuerza vertical a\(F\) una distancia a del soporte izquierdo. Dibuja un diagrama de cuerpo libre para
la viga, sustituyendo los soportes por las fuerzas de reacción\(R_1\) y\(R_2\) que ejerzan sobre el
haz. Resolver por las fuerzas de reacción en términos de\(F, a\), y\(L\).
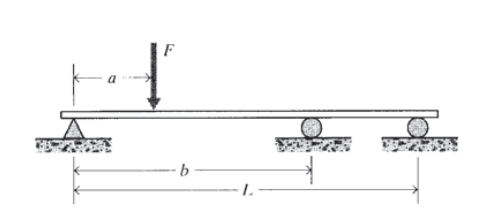
Ejercicio\(\PageIndex{2}\)
Se agrega un tercer soporte a la viga del problema anterior. Dibuja el diagrama de cuerpo libre para este caso y escribe las ecuaciones de equilibrio disponibles para resolver las fuerzas de reacción en cada soporte. ¿Es posible resolver para todas las fuerzas de reacción?
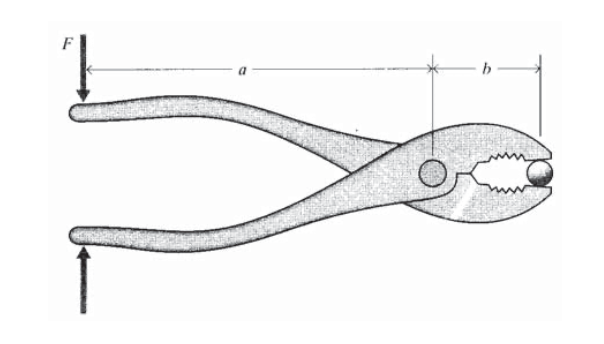
Ejercicio\(\PageIndex{3}\)
Los mangos de un par de alicates están cuadrados con una fuerza F. Dibuje un diagrama de cuerpo libre para uno de los brazos de los alicates. ¿Cuál es la fuerza que se ejerce sobre un objeto agarrado entre las caras de los alicates?
Ejercicio\(\PageIndex{4}\)
Un objeto de peso\(W\) se suspende de un marco como se muestra. ¿Cuál es la tensión en el cable de reentrenamiento\(AB\)?
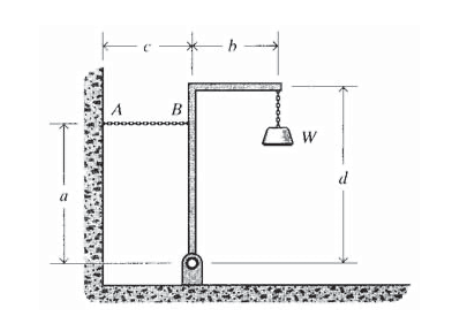
Ejercicio\(\PageIndex{5}\)
(a) - (h) Determinar la fuerza en cada elemento de las cerchas trazadas a continuación.
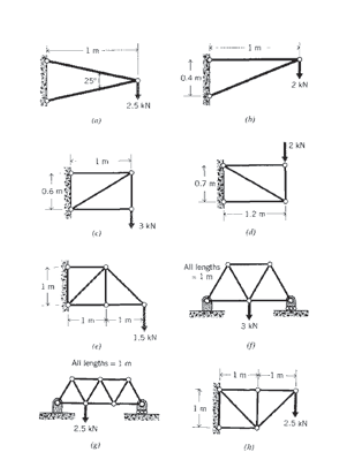
Ejercicio\(\PageIndex{6}\)
(a) - (h) Utilizando consideraciones geométricas, determinar la deflexión del punto de carga (el punto en el que se aplica la carga, en la dirección de la carga) para las cerchas en Ejercicio\(\PageIndex{5}\). Todos los elementos están construidos con varillas redondas de acero al carbono de 20 mm de diámetro.
Ejercicio\(\PageIndex{7}\)
(a) - (h) Igual que Ejercicio\(\PageIndex{6}\), pero usando el teorema de Castigliano.
Ejercicio\(\PageIndex{8}\)
(a) - (h) Igual que\ (\ PageIndex {6}\, pero usando análisis de elementos finitos.
Ejercicio\(\PageIndex{9}\)
Encuentre las fuerzas y deflexión del elemento en el punto de carga para la celosía mostrada, utilizando el método de su elección.
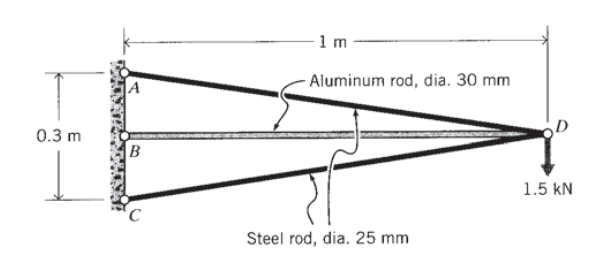
Ejercicio\(\PageIndex{10}\)
(a) - (c) Redactar las matrices globales de rigidez para las cerchas enumeradas a continuación, y resolver para las fuerzas y desplazamientos desconocidos.
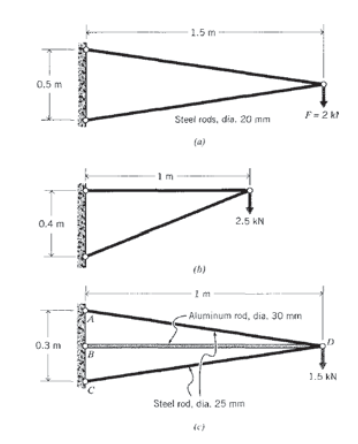
Ejercicio\(\PageIndex{11}\)
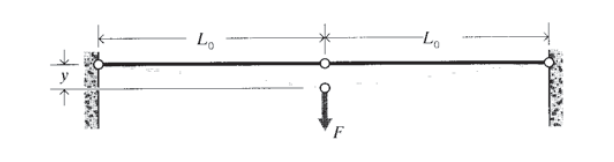
Dos elementos de celosía de igual longitud inicial\(L_0\) están conectados horizontalmente. Suponiendo que los elementos permanezcan linealmente elásticos en todas las deformaciones, determinar la deflexión\(y\) hacia abajo en función de una carga\(F\) aplicada transversalmente a la articulación.
