6.1: Rendimiento y Flujo de Plástico

Introducción

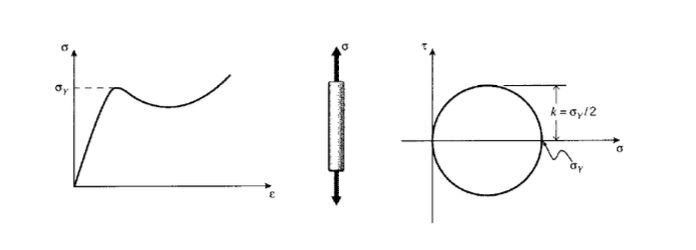
En nuestra visión general de la curva tensión-deformación en el Módulo 4, describimos el rendimiento como un reordenamiento molecular permanente que comienza con un esfuerzo suficientemente alto, denotado\(\sigma_Y\) en la Figura 1. El proceso de producción es muy dependiente del material, estando relacionado directamente con la movilidad molecular. A menudo es posible controlar el proceso de producción optimizando el procesamiento de materiales de una manera que influya en la movilidad. El poliestireno de uso general, por ejemplo, es un plástico débil y quebradizo que a menudo se le atribuye la reputación de dar a los plásticos una reputación de calumnia que plagó a la industria durante años. Esto ocurre porque el poliestireno a temperatura ambiente tiene tan poca movilidad molecular que experimenta fractura quebradiza a tensiones menores que las necesarias para inducir rendimiento con su flujo dúctil asociado. Pero cuando ese mismo material se mezcla con partículas de caucho de tamaño y composición adecuados, se vuelve tan resistente que se usa para cascos de bateo y juguetes infantiles ultrarduraderos. Esta magia se realiza mediante el control del proceso de ceder. El control de rendimiento para equilibrar la resistencia contra la tenacidad es uno de los aspectos más importantes de la ingeniería de materiales para aplicaciones estructurales, y todos los ingenieros deben ser conscientes de las posibilidades.

Figura 1: Estrés\(\sigma_Y\) de fluencia determinado por el método de desplazamiento de 0.2%.

Otra razón importante para entender el rendimiento es más prosaico: si no se permite que el material ceda, no es probable que falle. Esto no es cierto para los materiales quebradizos como las cerámicas que se fracturan antes de que cedan, pero en la mayoría de los materiales estructurales más duros no se producen daños antes del rendimiento. Es una práctica de diseño común dimensionar la estructura para mantener las tensiones en el rango elástico, corto de rendimiento por un factor de seguridad adecuado. Por lo tanto, necesitamos ser capaces de predecir cuándo ocurrirá el rendimiento en estados de estrés multidimensionales generales, dado un valor experimental de\(\sigma_Y\).

La fractura es impulsada por tensiones normales, actuando para separar un plano atómico de otro. El rendimiento, a la inversa, es impulsado por esfuerzos de corte, deslizando un plano a lo largo de otro. Estos dos mecanismos distintos se ilustran en la Figura 2. Por supuesto, los enlaces deben romperse durante el deslizamiento asociado con el rendimiento, pero a diferencia de la fractura se permite reformar en nuevas posiciones. Este proceso puede generar un cambio sustancial en el material, incluso conduciendo eventualmente a la fractura (como al doblar una varilla metálica de un lado a otro repetidamente para romperla). La deformación “plástica” que subyace al rendimiento es esencialmente un proceso de flujo viscoso, y sigue leyes cinéticas bastante similares a las de los líquidos. Al igual que el flujo en líquidos, el flujo de plástico generalmente se realiza sin cambio de volumen, correspondiente a la relación de Poisson\(ν = 1/2\).

Figura 2: El agrietamiento es causado por tensiones normales (a), el deslizamiento es causado por esfuerzos cortantes (b).

Estados de tensión multiaxial

El límite elástico generalmente\(\sigma_Y\) se determina en una prueba de tracción, donde actúa una sola tensión uniaxial. Sin embargo, el ingeniero debe ser capaz de predecir cuándo ocurrirá el rendimiento en situaciones de la vida real más complicadas que involucran tensiones multiaxiales. Esto se hace mediante el uso de un criterio de rendimiento, una observación derivada de la evidencia experimental en cuanto a lo que se trata del estado de estrés que causa el rendimiento. Uno de los criterios más simples, conocido como esfuerzo cortante máximo o criterio de Tresca, establece que el rendimiento se produce cuando el esfuerzo cortante máximo alcanza un valor crítico\(\tau_{\max} = k\). El valor numérico de\(k\) para un material dado podría determinarse directamente en una prueba de cizallamiento puro, como la torsión de un eje circular, pero también se puede encontrar indirectamente a partir de la prueba de tensión también. Como se muestra en la Figura 3, el círculo de Mohr muestra que el esfuerzo cortante máximo actúa en un plano\(45^{\circ}\) alejado del eje de tracción, y es la mitad del esfuerzo de tracción en magnitud; entonces\(k = \sigma_Y/2\).

En casos de tensión plana, el círculo de Mohr da el esfuerzo cortante máximo en ese plano como la mitad de la diferencia de las tensiones principales:

\[\tau_{\max} = \dfrac{\sigma_{p1} - \sigma_{p2}}{2}\]

Figura 3: Construcción del círculo de Mohr para rendimiento en tensión uniaxial.

Ejemplo\(\PageIndex{1}\)

Usando\(\sigma_{p1} = \sigma_{\theta} = pr/b\) y\(\sigma_{p2} = \sigma_{z} = pr/2b\) en 6.1.1, el esfuerzo cortante en un recipiente a presión cilindrico con extremos cerrados es (Ver Módulo 6)

 

donde el\(\theta_z\) subíndice indica un esfuerzo cortante en un plano tangencial a la pared del vaso. En base a esto, podríamos esperar que el recipiente a presión ceda cuando

\(\tau_{\max , \theta_z} = k = \dfrac{sigma_Y}{2}\)

que ocurriría a una presión de

\(p_Y = \dfrac{4b\tau{\max , \theta_z}}{r} \overset{?}{=} \dfrac{2b\sigma_Y}{r}\)

Sin embargo, este análisis es un error, como puede verse dibujando los círculos de Mohr no sólo para el\(\theta_z\) plano sino para los\(rz\) planos\(\theta_r\) y así como se muestra en la Figura 4.

Figura 4: Tensiones principales y círculo de Mohr para recipiente a presión de extremo cerrado

Se considera que las tensiones cortantes en el\(\theta_r\) plano son el doble de las del\(\theta_z\) plano, ya que en el\(\theta_r\) plano la segunda tensión principal es cero:

 

Por lo tanto, el rendimiento ocurrirá en el\(\theta_r\) plano a una presión de\(b\sigma_Y/r\), la mitad del valor necesario para causar rendimiento en el\(\theta_z\) plano. No considerar las tensiones cortantes que actúan en esta tercera dirección conduciría a un buque seriamente subdiseñado.

Situaciones similares a este ejemplo ocurren en tensión plana siempre que las tensiones principales en el\(xy\) plano sean del mismo signo (tanto de tracción como de compresión). El esfuerzo cortante máximo, que controla el rendimiento, es la mitad de la diferencia entre los esfuerzos principales; si ambos son del mismo signo, se producirá un esfuerzo cortante aún mayor en el plano perpendicular que contiene el mayor de los esfuerzos principales en el plano xy.

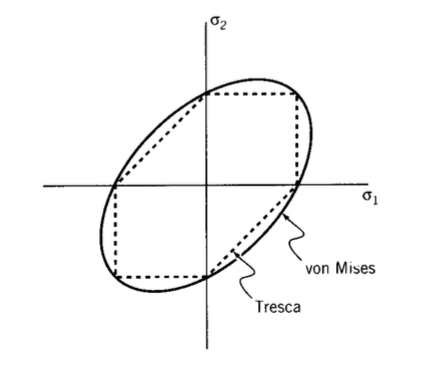
Este concepto se puede utilizar para dibujar un “locus de rendimiento” como se muestra en la Figura 5, una envolvente en\(\sigma_1 - \sigma_2\) coordenadas fuera de la cual se predice el rendimiento. Este lugar obviamente cruza los ejes de coordenadas en valores correspondientes al límite elástico por tracción\(\sigma_Y\). En los cuadrantes I y III las tensiones principales son del mismo signo, por lo que de acuerdo con el criterio de esfuerzo cortante máximo el rendimiento se determina por la diferencia entre la tensión principal mayor y cero. En los cuadrantes II y IV el locus viene dado por\(\tau_{\max} = |\sigma_1 - \sigma_2|/2 = \sigma_Y /2\), so\(\sigma_1 - \sigma_2\) = const; esto da líneas diagonales rectas que van de\(\sigma_Y\) un eje a\(\sigma_Y\) otro.

Figura 5. Lugar de rendimiento para el criterio de esfuerzo cortante máximo.

Ejemplo\(\PageIndex{2}\)

Figura 6: (a) Eje circular sometido a torsión y tensión simultáneas. b) Construcción del círculo de Mohr.

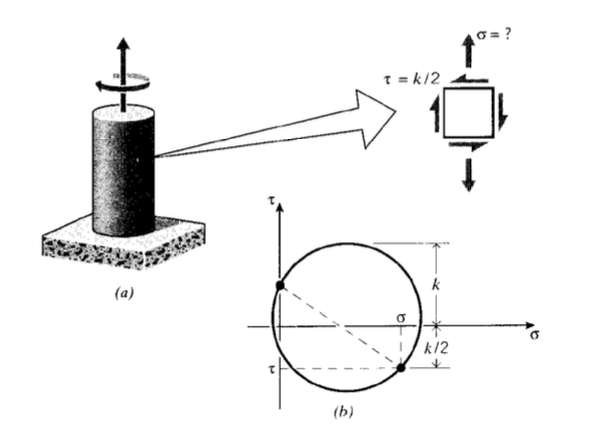
Un eje circular se somete a un par de torsión de la mitad que se necesita para causar cesiones como se muestra en la Figura 6; ahora preguntamos qué esfuerzo de tracción podría aplicarse simultáneamente sin causar rendimiento.

Se dibuja un círculo de Mohr con esfuerzo cortante\(\tau = k/2\) y tensión de tracción desconocida\(\sigma\). Usando el criterio de rendimiento de cizallamiento máximo de Tresca, el rendimiento ocurrirá cuando\(\sigma\) sea tal que

\(\tau_{\max} = k = \sqrt{(\dfrac{\sigma}{2})^2 + (\dfrac{k}{2})^2}\)

\(\sigma = \sqrt{3} k\)

El criterio de Tresca es conveniente de usar en la práctica, pero a menudo se puede obtener un ajuste algo mejor a los datos experi- mentales a partir del criterio “von Mises”, en el que la fuerza impulsora para el rendimiento es la energía de deformación asociada a los componentes desviatorios del estrés. La tensión de von Mises (también llamada tensión equivalente o efectiva) se define como

 

En términos de los principales destaca esto es

 

donde las diferencias de esfuerzos entre paréntesis son proporcionales a las tensiones máximas de cizallamiento en los tres planos principales (Algunos autores utilizan un factor distinto de 1/2 dentro del radical. Esto es inmaterial, ya que será absorbido por el cálculo del valor crítico de\(\sigma_M\)) (Dado que las cantidades son cuadradas, el orden de tensiones dentro de los paréntesis no es importante.) El estrés Mises también se puede escribir en forma compacta en términos de la segunda invariante del tensor de tensión desviatoria\(\Sigma_{ij}\):

\[\sigma_M = \sqrt{3\Sigma_{ij} \Sigma_{ij}/2}\]

Se puede demostrar que esto es proporcional a la energía de deformación de distorsión total en el material, y también al esfuerzo cortante τoct en el plano “octaédrico” orientado igualmente a los ejes 1-2-3. La tensión de von Mises es la fuerza impulsora del daño en muchos materiales de ingeniería dúctil, y se calcula rutinariamente por la mayoría de los códigos comerciales de análisis de tensión de elementos finitos.

El valor del esfuerzo de von Mises\(\sigma_{M,Y}\) necesario para causar el rendimiento se puede determinar a partir del límite elástico por tracción\(\sigma_Y\), ya que en tensión en el punto de fluencia tenemos\(\sigma_1 = \sigma_Y\),\(\sigma_2 = \sigma_3 = 0\). Entonces

 

Por lo tanto, el valor del esfuerzo de von Mises necesario para causar el rendimiento es el mismo que el esfuerzo de fluencia por tracción simple.

El límite elástico por cizallamiento se\(k\) puede encontrar de manera similar insertando las tensiones principales correspondientes a un estado de cizallamiento puro en la ecuación de Mises. Usando\(k = \sigma_1 = -\sigma_3\) y\(\sigma_2 = 0\), tenemos

 

\(k = \dfrac{\sigma_Y}{\sqrt{3}}\)

Tenga en cuenta que este resultado es diferente al caso Tresca, en el que tuvimos\(k = \sigma_Y/2\).

El criterio de von Mises también se puede trazar como un locus de rendimiento. Así como el criterio de Tresca, debe pasar por\(\sigma_Y\) encima de cada eje. Sin embargo, se traza como elipse en lugar de la forma prismática del criterio de Tresca (ver Figura 7).

Figura 7: Locus de rendimiento para el criterio de von Mises.

Efecto de la presión hidrostática

Dado que en la discusión hasta ahora el rendimiento se ha regido únicamente por el esfuerzo cortante, no ha importado si un esfuerzo uniaxial es compresivo o de tracción; el rendimiento ocurre cuando\(\sigma = \pm \sigma_Y\). Esto corresponde al componente hidrostático de la tensión\(-p = (\sigma_x + \sigma_y + \sigma_z)/3\) que no tiene influencia en el rendimiento, lo que se observa experimentalmente como válido para deslizamiento en sistemas metálicos. Los polímeros, sin embargo, son mucho más resistentes al rendimiento en estados de tensión compresiva que en tensión. Los movimientos atomísticos subyacentes al deslizamiento en los polímeros pueden considerarse como que requieren “volumen libre” a medida que los segmentos moleculares se mueven, y este volumen libre se ve disminuido por las tensiones de compresión. Por lo tanto, es difícil formar polímeros sólidos mediante el procesamiento de deformación, como el estampado y la forja, de la misma manera que se puede conformar el acero; esta es una de las razones por las que la gran mayoría de los paneles de carrocería de automóviles continúan hechos de acero en lugar de plástico.

Figura 8: Efecto de la presión sobre la envoltura de rendimiento de von Mises.

Esta dependencia de la tensión hidrostática se puede modelar modificando el criterio de rendimiento para indicar que el rendimiento ocurre cuando

\[\tau_{\max} \text{ or } \sigma_M \ge r_0 + A_p\]

donde\(\tau_0\) y\(A\) son constantes. A\(p\) medida que aumenta (el componente hidrostático de la tensión se vuelve más positivo) el esfuerzo cortante necesario para el rendimiento también se vuelve mayor, ya que hay menos volumen libre y más obstáculos para el movimiento molecular. El efecto de esta modificación es deslizar la elipse de von Mises para extenderse menos en el cuadrante I y más en el cuadrante III como se muestra en la Figura 8. Esto muestra gráficamente que se necesitan mayores tensiones para el rendimiento en la compresión y menores tensiones en tensión.

Figura 9: Una locura en poliestireno (de R. Kambour, “Crazing”, Encyclopedia of Polymer Science and Engineering, Wiley-Interscience, 1991).

Varios polímeros vítreos amorfos, especialmente poliestireno, polimetilmetacrilato y policarbonato, están sujetos a un mecanismo de rendimiento denominado “agrietamiento” en el que se crean huecos alargados largos dentro del material mediante un proceso de cavitación por tracción. La Figura 9 muestra una locura en poliestireno, cultivada en fluido plastificante cerca\(T_g\). Los huecos, o grietas, tienen aproximadamente 1000A de espesor y micrones o más de longitud, y parecen visualmente ser muy parecidos a los convencionales

grietas. Se diferencian de las grietas, sin embargo, en que las caras anchas de las fisuras están abarcadas por una gran cantidad de fibrillas alargadas que se han extraído del polímero a medida que se abre la locura. La formación de fibrillas requiere flujo de cizallamiento, pero el proceso también es muy dependiente del volumen libre. Se ha propuesto un criterio de esfuerzo multiaxial exitoso para el agrietamiento que incorpora ambas características (S. Sternstein y L. Ongchin, Polymer Preprints, 10, 1117, 1969.) de la forma

 

El lado izquierdo de esta relación es proporcional al esfuerzo cortante, y el denominador en el segundo término en el lado derecho está relacionado con el componente hidrostático de la tensión. A medida que aumenta la tensión hidrostática, disminuye el cizallamiento necesario para causar agrietamiento. Los parámetros\(A\) y\(B\) son ajustables, y ambos dependen de la temperatura. Esta relación se traza como un batwing en el diagrama de locus de rendimiento como se ve en la Figura 10, acercándose a una\(45^{\circ}\) diagonal dibujada a través de los cuadrantes II y IV. El agrietamiento ocurre a la derecha de la curva; tenga en cuenta que el agrietamiento nunca ocurre en los campos de esfuerzo compresivo.

Figura 10: Las envolturas de Sternstein para agrietamiento y rendimiento por cizallamiento inhibido por presión.

El agrietamiento es un mecanismo de rendimiento, pero también precipita la fractura quebradiza a medida que aumenta la altura de la grieta y las fibrillas se rompen. Por lo tanto, el punto en el que el locus de la fisura cruza el lugar de producción de cizallamiento es un tipo de transición dúctil-quebradiza inducida mecánicamente, ya que el modo de falla cambia de deformación por cizallamiento a fragilización de grietas. Los agentes ambientales como la acetona que expanden el volumen libre en estos polímeros exacerban en gran medida la tendencia a la fragilidad de las grietas. Por el contrario, modificaciones como las inclusiones de partículas de caucho que estabilizan las grietas y evitan que se conviertan en verdaderas grietas pueden proporcionar una tenacidad notable. Las partículas de caucho no solo estabilizan las fisuras, sino que también causan un gran aumento en el número de grietas, por lo que la absorción de energía de la formación de grietas también puede aumentar la dureza. Esta es la base del “poliestireno de alto impacto”, o HIPS, mencionado al inicio de este capítulo.

Efecto de la velocidad y la temperatura

Se puede considerar que el proceso de rendimiento compite con la fractura, y cualquier proceso que tenga los requisitos de esfuerzo más bajos dominará. A medida que el material se hace cada vez menos móvil, por ejemplo al bajar la temperatura o aumentar el número y la estanqueidad de los enlaces químicos, el rendimiento se vuelve cada vez más difícil. El proceso de fractura suele depender mucho menos de la movilidad. Tanto el rendimiento como los esfuerzos de fractura suelen aumentar con la disminución de la temperatura, pero el rendimiento es más dependiente de la temperatura (ver Figura 11). Esto implica que por debajo de una temperatura crítica (llamada temperatura de transición dúctil-quebradiza TDB) el material se fracturará antes de que ceda. Varias fallas notables en barcos y ductos se han producido durante las temperaturas invernales cuando los aceros utilizados en su fabricación se estresaron por debajo de su TDB y por lo tanto no pudieron resistir el crecimiento catastrófico de grietas. En los polímeros, la temperatura de transición dúctil-quebradiza suele ser coincidente con la temperatura de transición vítrea. Claramente, necesitamos un modelo de ingeniería capaz de mostrar cómo el rendimiento depende de la temperatura, y a continuación se describe un enfoque popular.

Los procesos de rendimiento son activados térmicamente, movimientos impulsados por tensión, al igual que el flujo de líquidos viscosos. Incluso sin entrar en muchos detalles en cuanto a los detalles de los movimientos, es posible anotar expresiones bastante efectivas para la dependencia de estos movimientos de la velocidad de deformación y la temperatura. En la vista Eyring de los procesos activados térmicamente, se\(E_Y^*\) debe superar una barrera de energía para que el movimiento continúe. (Utilizaremos el superíndice de asterisco para indicar la activación

Figura 11: Ilustración esquemática de la dependencia de la temperatura del rendimiento y la tensión de fractura.

parámetros, y el\(Y\) subíndice aquí indica el proceso de rendimiento.) Una tensión actúa para bajar la barrera cuando actúa en la dirección del flujo, y para elevarla cuando se opone al flujo.

Consideremos ahora una prueba de tasa de deformación constante (\(\dot{\epsilon}\)= const), en la que la tensión aumenta hasta que se produce el rendimiento en\(\sigma = \sigma_Y\). En el punto de rendimiento tenemos\(d\sigma/d\epsilon = 0\), por lo que se logra un estado fluido en el que se puede producir un incremento de deformación sin un incremento incremental correspondiente en la tensión. Análogamente con las teorías de velocidad para el flujo viscoso, se puede escribir una ecuación de tasa Eyring para el proceso de rendimiento como

\[\dot{\epsilon} = \dot{\epsilon_0} \exp \dfrac{-(E_Y^* - \sigma_Y V^*)}{kT}\]

Aquí\(k\) está la constante de Boltzman y\(V^*\) es un factor que rige la efectividad del estrés en la reducción de la barrera de activación. Debe tener unidades de volumen para que el producto\(\sigma_Y V^*\) tenga unidades de energía, y se denomina el “volumen de activación” del proceso. Tomando registros y reordenando,

\(\dfrac{\sigma_Y}{T} = \dfrac{E_Y^*}{V*T} + \dfrac{k}{V^*} \ln \left(\dfrac{\dot{\epsilon}}{\dot{\epsilon_0}}\right)\)

Por lo tanto, las gráficas de\(\sigma_Y/T\) versus\(\ln \dot{\epsilon}\) deben ser lineales con una pendiente\(k/V^*\) como se ve en la Figura 12, a partir de la cual se puede calcular el volumen de activación. El espaciamiento horizontal entre dos líneas a diferentes temperaturas\(T_1\) y\(T_2\) da la energía de activación:

 

Los volúmenes aparentes de activación en polímeros son del orden de 5000\(\dot{A}\), mucho más grandes que una sola unidad repetitiva. Esto se toma para indicar que el rendimiento en polímeros implica el movimiento cooperativo de varios cientos de unidades repetidas.

Ejemplo\(\PageIndex{3}\)

El límite elástico para policarbonato se reporta a 60 MPa a temperatura ambiente (\(23^{\circ}C\)=\(296^{\circ}K\)), y deseamos conocer su valor en\(0^{\circ}C\) (273\(^{\circ}K\)), manteniendo la misma tasa de deformación.

Esto se puede lograr escribiendo la Ecuación 4 dos veces, una por cada temperatura, y luego dividiendo una por la otra. Los parámetros\(\dot{\epsilon}\) y\(\dot{\epsilon_0}\) cancelar, dejando

 

A partir de los datos de la Figura 12, los parámetros de activación del rendimiento son\(E_Y^* = 309\ kJ/mol\),\(V^* = 3.9 \times 10^{-3}\ m^3/mol\). Usando estos junto con\(R = 8.314\ J/mol\) y\(\sigma_Y^{296} = 60 \times 10^6\ N/m^2\), tenemos

Figura 12: Gráfica de Eyring que muestra la dependencia del límite elástico de la temperatura y la velocidad de deformación en policarbonato (de N.G. McCrum, C.P Buckley y C.B. Bucknall, Principles of Polymer Engineering, Oxford University Press, 1988).

\(\sigma_Y^{273} = 61.5\ MPa\)

Plasticidad continua

La teoría de la plasticidad, que busca determinar tensiones y desplazamientos en estructuras todas o parte de las cuales han sido estresadas más allá del límite de rendimiento, es un aspecto importante de la mecánica de sólidos. La situación es tanto material como geométricamente no lineal, por lo que no es una empresa trivial. Sin embargo, en áreas como la formación de metales, la teoría de la plasticidad ha proporcionado información valiosa. Vamos a esbozar sólo algunos aspectos de este campo en los siguientes párrafos, para introducir algunos de los conceptos fundamentales que el lector puede extender en futuros estudios.

Deformación plástica

Una idealización útil en el modelado del comportamiento plástico lleva al material a ser linealmente elástico hasta el límite de fluencia como se muestra en la Figura 13, y luego “perfectamente plástico” en deformaciones más allá del rendimiento. Las deformaciones hasta el rendimiento (la línea entre puntos\(a\) y\(b\)) son recuperables, y el material se descarga a lo largo de la misma línea elástica que siguió durante la carga; esta es la respuesta elástica convencional. Pero si el material se deforma más allá del rendimiento (punto\(b\)), el esfuerzo “plástico” más allá de b se lleva a cabo a tensión constante y es irrecuperable. Si el material se tensa hasta apuntar\(c\) y luego se descarga, sigue el camino cd (una línea paralela a la línea elástica original\(ab\)) en lugar de regresar a lo largo\(cba\). Cuando la tensión se ha llevado a cero (punto\(d\)), la deformación plástica ad permanece como una deformación residual.

Figura 13: La idealización elástica-perfectamente plástica de la deformación plástica.

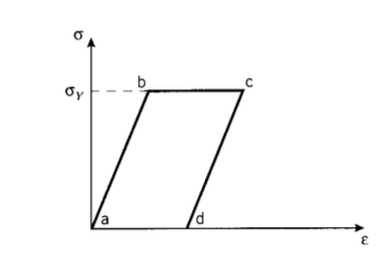
La deformación plástica puede generar tensiones “residuales” en las estructuras, tensiones internas que permanecen incluso después de que se eliminan las cargas externas. Para ilustrar esto, considere dos varillas que tienen diferentes curvas de tensión-deformación, conectadas en paralelo (por lo que sus deformaciones son siempre iguales) como se muestra en la Figura 14. Cuando las varillas son tensas hasta el límite de elasticidad de la varilla B (punto a en el eje de deformación), la varilla\(A\) habrá experimentado una cantidad de deformación plástica permanente\(\epsilon^p\). Cuando se elimina la carga aplicada, la varilla se\(B\) descarga a lo largo de su curva original de tensión-deformación, pero la varilla\(A\) sigue una trayectoria paralela a su línea elástica original. Cuando la varilla\(A\) alcanza tensión cero (punto\(b\)), la varilla\(B\) seguirá estando en tensión (punto\(c\)). Para que la carga transmitida por las varillas juntas llegue a cero, la varilla\(B\) tirará de la varilla\(A\) a compresión hasta que\(-\sigma_B = -\sigma_A\) lo indiquen los puntos\(d\) y\(e\). Las tensiones residuales se dejan en las varillas, y el conjunto en su conjunto se deja con una tensión de tracción residual.

Figura 14: Deformación plástica del conjunto de dos barras.

La tensión residual compresiva puede ser valiosa si la estructura debe soportar cargas de tracción. De manera similar a cómo se puede usar el temple rápido para hacer vidrios de seguridad al poner las superficies en compresión, la deformación plástica se puede usar para crear tensiones de compresión favorables. Una técnica famosa de este tipo se llama “autofrettage”; este es un método utilizado para fortalecer los cañones de cañón contra el estallido al presurizarlos desde el interior para llevar la porción interna del cañón a la gama de plástico. Cuando se elimina la presión, las porciones internas se dejan con una tensión residual compresiva al igual que con la barra\(A\) en el ejemplo anterior.

trefilado

Para cuantificar el proceso de flujo de plástico con más detalle, considere a continuación el “trefilado” del alambre (G.W. Rowe, Elements of Metalworking Theory, Edward Arnold, Londres, 1979.), en el que se tira del alambre a través de una matriz reductora para reducir su área de sección transversal de\(A_0\) a\(A\) como se muestra en la Figura 15. Dado que el volumen se conserva durante la deformación plástica, esto corresponde a un alargamiento axial de\(L/L_0 = A_0/A\). Considerando que el estado de estrés es simple tensión uniaxial, tenemos

Figura 15: trefilado.

\(\sigma_1 = \sigma_Y, \sigma_2 = \sigma_3 = 0\)

donde 1 denota la dirección a lo largo del cable y 2 y 3 son las direcciones transversales. El trabajo realizado en el estiramiento del alambre en un incremento de longitud dL, por unidad de volumen de material, es

\(dU = \dfrac{dW}{AL} = \dfrac{\sigma_Y A dL}{AL}\)

Integrando esto de\(L_0\)\(L\) a para obtener el trabajo total:

\(U = \int_{L_0}^{L} dU = \dfrac{FdL}{AL} = \sigma_Y \ln \dfrac{L}{L_0}\)

La cantidad\(ln(L/L_0)\) es la deformación logarítmica\(\epsilon_T\) introducida en el Módulo 4 (Curvas de Estrés-Tensión).

Ejemplo\(\PageIndex{1}\)

La deformación logarítmica se puede escribir en términos de aumento de longitud o reducción de área, debido a la constancia de volumen durante la deformación plástica:\(\epsilon_T = \ln (L/L_0) = \ln (A_0/A)\). En términos de reducción de diámetro, la relación\(A = \pi d^2/4\) conduce a

\(e_T = \ln (\dfrac{\pi d_0^2/4}{\pi d^2/4}) = 2\ln (\dfrac{d_0}{d})\)

Tomando el tamaño de celda de perlita para encogerse proporcionalmente con el diámetro, esperamos que la resistencia\(\sigma_f\) del alambre varíe de acuerdo con la relación Hal-Petch con\(1/\sqrt{d}\). La relación entre la resistencia del alambre y la deformación de estirado logarítmico es entonces

\(\sigma_f \propto \dfrac{\exp (\epsilon_T/4)}{\sqrt{d_0}}\)

El trabajo realizado por la fuerza de tracción constante\(F\) en el estirado de una longitud inicial\(L_0\) de alambre a una nueva longitud\(L\) es\(W = FL\). Esto debe ser igual al trabajo por unidad de volumen realizado en la matriz, multiplicado por el volumen total de alambre:

\(FL = (AL) \sigma_Y \ln \dfrac{L}{L_0}\)

Escrito en términos de reducción de área, esto es

\(F = A \sigma_Y \ln \dfrac{A_0}{A}\)

Este resultado simple es útil para estimar los requisitos del trefilado, aunque descuida el complicado campo de flujo real dentro de la matriz y la influencia de la fricción en las paredes de la matriz. Tanto la fricción en la superficie como las restricciones para fluir dentro del campo elevan la fuerza necesaria en el dibujo, pero el presente análisis sirve para establecer una aproximación de límite inferior. A menudo se escribe en términos de la tensión de dibujo\(\sigma_1 = F/A\) y la relación de reducción de área\(r = (A_0 - A)/A_0 = 1 - (A/A_0)\):

 

Tenga en cuenta que el esfuerzo de estiramiento para una reducción de área pequeña es menor que el límite elástico por tracción. De hecho, la reducción máxima de área que se puede lograr en una sola pasada se puede estimar resolviendo para el valor de\(r\) lo cual lleva el esfuerzo de estirado hasta el valor del límite elástico, que obviamente no puede superar. Este cálculo da

 

De ahí que la reducción máxima de área sea de aproximadamente 63%, suponiendo una lubricación perfecta en la matriz. Este tratamiento de límite inferior da un resultado optimista, pero no está lejos de la reducción de aproximadamente el 50% que se suele utilizar como límite práctico. Si el material se endurece durante el estirado, la reducción máxima puede ser ligeramente mayor.

Campos Slip-line

En los casos de deformación plana, existe una técnica gráfica llamada teoría slip-line (W. Johnson y P.B. Mellor, Plasticidad para ingenieros mecánicos, Van Nostrand Co., Nueva York, 1962) que permite un examen más detallado de los campos de flujo de plástico y las cargas necesarias para crearlos. Se pueden incluir restricciones de fricción y flujo interno, por lo que se obtienen aproximaciones de límite superior que proporcionan estimaciones más conservadoras de las fuerzas necesarias en la deformación. Se necesita una experiencia considerable para dominar este método, pero a continuación se esbozarán algunas de las ideas básicas.

Considere la deformación plana en el plano 1-3, sin deformación en la dirección 2. Hay un estrés de Poisson en la dirección 2, dado por

 

Dado que\(v = 1/2\) en flujo de plástico,

\(\sigma_2 = \dfrac{1}{2} (\sigma_1 + \sigma_3)\)

El componente hidrostático de la tensión es entonces

\(p = \dfrac{1}{3} (\sigma_1 + \sigma_2 + \sigma_3) = \dfrac{1}{2} (\sigma_1 + \sigma_3) = \sigma_2\)

De ahí que la tensión de Poisson\(\sigma_2\) en la dirección de deformación cero sea el promedio de las otras dos tensiones\(\sigma_1\) y\(\sigma_2\), y también igual al componente hidrostático de la tensión. El estado de tensión se puede especificar en términos del esfuerzo cortante máximo, que es justo\(k\) durante el flujo de plástico, y la presión hidrostática superpuesta\(p\):

\(\sigma_1 = -p + k\),\(\sigma_2 = -p\),\(\sigma_3 = -p -k\)

Dado que el esfuerzo cortante es igual a\(k\) todas partes, el problema es determinar las direcciones de\(k\) (la dirección del cizallamiento máximo, a lo largo de la cual se produce el deslizamiento), y la magnitud de\(p\).

La técnica gráfica consiste en esbozar líneas que se encuentran a lo largo de las direcciones de\(k\). Dado que las tensiones máximas de corte actúan sobre dos planos ortogonales, habrá dos conjuntos de estas líneas, siempre perpendiculares entre sí y denominadas\(\alpha\) -líneas y\(\beta\) -líneas. La dirección de estas líneas se especifica mediante un ángulo de inclinación\(\phi\). Cualquier inclinación conveniente puede ser utilizada para el\(\phi = 0\) dato, y la identificación de\(\alpha\) - vs.\(\beta\) -líneas es tal que hace que el esfuerzo cortante sea positivo de acuerdo con la convención habitual. Como la presión\(p\) varía de punto a punto, existe una variación correspondiente del ángulo\(\phi\), dada por las ecuaciones de Hencky como

\(p + 2k\phi = C_1 =\)constante, a lo largo\(\alpha\) de una línea

\ (\ beta\) -línea</p lt-eng-44550">

De ahí que la presión se pueda determinar a partir de la curvatura de las líneas de deslizamiento, una vez que se conoce la constante.

El campo slip-line debe obedecer ciertas restricciones en los límites:

1. Superficies libres: Ya que no puede haber tensión normal a una superficie libre, podemos poner\(\sigma_3 = 0\) ahí y luego

\(p = k, \sigma_1 = -p -k = -2k\)

Por lo tanto, se sabe que la presión es solo el límite elástico de cizallamiento en una superficie libre. Además, dado que las direcciones normales y tangenciales a la superficie son direcciones principales, las direcciones de cizallamiento máximo deben estar inclinadas\(45^{\circ}\) hacia la superficie.

2. Superficie sin fricción: El esfuerzo cortante debe ser tangencial cero a una superficie sin fricción, lo que nuevamente significa que las direcciones tangencial y normal deben ser direcciones principales. De ahí que las líneas de deslizamiento deben encontrarse con la superficie en\(45^{\circ}\). No obstante, en general habrá una tensión actuando normal a la superficie, así\(\sigma_3 \ne 0\) y así no\(p\) será igual a\(k\).

3. Superficie perfectamente rugosa: Si la fricción es tan alta como para evitar cualquier movimiento tangencial en la superficie, el cizallamiento debe ser máximo en una dirección que también sea tangencial a la superficie. Un conjunto de líneas de deslizamiento debe ser tangencial a la superficie, y el otro conjunto normal a ella.

Figura 16: Construcción de línea deslizante para una indentación plana.

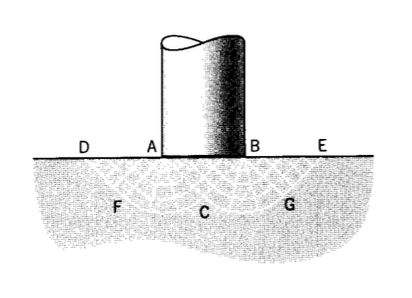
Considera que un indentador plano de ancho b se presiona en un bloque semi-infinito, con fricción insignificante (ver Figura 16). Dado que las líneas deslizantes deben encontrarse con la superficie del indentador en\(45^{\circ}\), podemos dibujar un campo de flujo triangular\(ABC\). Dado que todas las líneas en esta región son rectas, no puede haber variación en la presión\(p\), y el campo es uno de “estado constante”. Esta no puede ser la extensión completa del campo, sin embargo, ya que estaría restringido tanto vertical como lateralmente por metal rígido. El campo debe extenderse a las superficies libres adyacentes al punzón, de manera que el movimiento hacia abajo debajo del punzón pueda ser compensado por el flujo ascendente adyacente al mismo. Se\(BEG\) agregan dos regiones\(ADF\) triangulares más que satisfacen las condiciones de contorno en superficies libres, y estas están conectadas a las regiones triangulares centrales por “ventiladores”\(AFC\) y\(BCG\). Los ventiladores son muy útiles en construcciones de líneas deslizantes; normalmente se centran en singularidades como puntos\(A\) y\(B\) donde no hay una normal definida a la superficie.

La presión sobre el punzón necesaria para establecer este campo se puede determinar a partir de las líneas de deslizamiento, y este es uno de sus principales usos. Dado que BE es una superficie libre,\(\sigma_3 = 0\) ahí y\(p = k\). La presión permanece constante a lo largo de la línea\(EG\) ya que\(\phi\) no cambia, pero a medida que\(\phi\) disminuye a lo largo de la curva\(GC\) (la línea se curva en sentido horario), la presión debe aumentar de acuerdo con la ecuación de Hencky En el punto\(C\) se ha girado por\(-\pi/2\) lo que la presión hay

\(p_C + 2k\phi = p_C + 2k (-\dfrac{\pi}{2}) =\)constante =\(p_G = k\)

\(p_C = k(1 +\pi)\)

La presión permanece sin cambios a lo largo de las líneas\(CA\) y\(CB\), así la presión a lo largo de la cara del punzón también\(k(1 + \pi)\) La tensión total que actúa hacia arriba en la cara del punzón es por lo tanto

\(\sigma_1 = p +k =2k(1 + \dfrac{\pi}{2})\)

La relación entre la presión del punzón y el límite elástico a la tracción\(2k\) es

\(\dfrac{\sigma_1}{2k} = 1 + \dfrac{\pi}{2} = 2.571\)

El factor 2.571 representa el aumento sobre el límite elástico a la tracción causado por las restricciones geométricas en el campo de flujo bajo el punzón.

El Ensayo de Dureza Brinell es similar al escenario de rendimiento de punzón anterior, pero utiliza una esfera de acero duro en lugar de un indentador plano. La dureza Brinell\(H\) se calcula como la carga aplicada al punzón dividida por el área proyectada de la indentación. El análisis de la prueba Brinell difiere algo en geometría, pero produce un resultado no muy diferente al del punzón plano:

 

Esta relación es muy útil para estimar el límite elástico de los metales mediante ensayos simples de dureza de indentación no destructiva.

Ejercicio\(\PageIndex{1}\)

Un recipiente a presión abierto está construido de aluminio, con un diámetro de 0.3 m y un grosor de pared de 3 mm. (Abierto en este contexto significa que ambos extremos del recipiente están conectados a otras partes estructurales capaces de soportar la presión, como en una manguera conectada entre dos depósitos). Determinar la presión interna a la que cederá el recipiente de acuerdo con los criterios (a) Tresca y (b) von Mises.

Ejercicio\(\PageIndex{2}\)

Repita el problema anterior, pero con el recipiente a presión ahora cerrado.

Ejercicio\(\PageIndex{3}\)

Una placa de acero se recubre con una fina capa de aluminio en ambos lados a temperatura ambiente, y la temperatura luego se eleva. ¿A qué aumento de temperatura\(\Delta T\) cederá el aluminio?

Ejercicio\(\PageIndex{4}\)

Si la temperatura en el problema anterior se eleva\(40\{circ} C\) más allá del valor al que se produce el rendimiento, y posteriormente se vuelve a bajar a temperatura ambiente, ¿cuál es la tensión residual que queda en el aluminio?

Ejercicio\(\PageIndex{5}\)

La aleación de cobre se somete al estado de tensión\(\sigma_x = 100\)\(\sigma_y = -200\),,\(\tau_{xy} = 100\) (todo en MPa). Determinar si el rendimiento ocurrirá de acuerdo con los criterios de (a) Tresca y (b) von Mises.

Ejercicio\(\PageIndex{6}\)

Repetir el problema anterior, pero con el estado de estrés\(\sigma_x = 190\)\(\sigma_y = 90\),,\(\tau_{xy} = 120\) (todo en MPa).

Ejercicio\(\PageIndex{7}\)

Un tubo de pared delgada se coloca en tensión y torsión simultáneas, provocando un estado de tensión como se muestra aquí. Construir una parcela de\(\tau /\sigma_Y\) vs.\(\sigma /\sigma_Y\) a la que se producirá el rendimiento de acuerdo con los criterios de (a) Tresca y (b) von Mises. (\(\sigma\)es el límite elástico por tracción.)

Ejercicio\(\PageIndex{8}\)

Un eje de acero circular sólido es cargado por poleas de correa en ambos extremos como se muestra. Determinar el diámetro del eje requerido para evitar el rendimiento de acuerdo con el criterio de von Mises, con un factor de seguridad de 2.

Ejercicio\(\PageIndex{9}\)

Para el policarbonato, se encuentra que los parámetros cinéticos en 6.1.4 son\(\dot{\epsilon_0} = 448 s^{-1}\),\(E_Y^* = 309\ kJ/mol\), y\(V* = 3.9 \times 10^{-3}\ m^3/mol\). Encuentre el límite elástico\(\sigma_Y\) a una velocidad de deformación\(\dot{\epsilon} = 10^2 s^{-1}\) y temperatura\(40^{\circ}C\).

Ejercicio\(\PageIndex{10}\)

Los esfuerzos de fluencia (en MPa) se han medido a diversas velocidades de deformación y temperaturas de la siguiente manera:

	\(\dot{epsilon} = 10^{-3} s^{-1}\)	\(\dot{epsilon} = 10^{-1} s^{-1}\)
\(T = 0^{\circ} C\)	54.1	62.7
\(T = 40^{\circ} C\)	42.3	52.1

Determinar el volumen de activación para el proceso de rendimiento. ¿Qué significación física podría tener este parámetro?

Ejercicio\(\PageIndex{11}\)

El límite elástico de un polímero se mide para ser 20 MPa a una temperatura de 300K y una tasa de deformación de\(10^{-3}s^{-1}\). Cuando se duplica la tasa de deformación a partir de este valor, se observa que el límite elástico aumenta en un 10%. ¿Cuál es el volumen aparente de activación para el rendimiento en este caso?

Ejercicio\(\PageIndex{12}\)

Mostrar el estrés de von Mises se puede escribir en notación de índice como\(\sigma_M = \sqrt{3 \Sigma_{ij} \Sigma_{ij}/2}\)

Ejercicio\(\PageIndex{13}\)

Se probó una muestra de polietileno lineal en carga uniaxial a\(T = 23^{\circ} C\) y\(\dot{\epsilon} = 10^{-3}s^{-1}\). \(\sigma_Y\)Se encontró que el límite elástico fue de 30.0 MPa en tensión y 31.5 MPa en compresión. Determinar la constante presión-dependencia\(A\) en la Ecuación 3.

Ejercicio\(\PageIndex{14}\)

Un eje circular de radio R se somete a un par\(T\).

a) ¿Qué valor de\(T\) será lo suficientemente grande como para inducir rendimientos en la superficie exterior?

(b) A medida que el valor de\(T\) se incremente más allá del nivel encontrado en (a), determinar el radio re dentro del cual el material aún se encuentra en el rango elástico.

(c) ¿Qué valor de\(T\) hará que el eje sea completamente plástico; es decir\(r_e = 0\)?

Ejercicio\(\PageIndex{15}\)

Un marco de celosía de dos elementos está construido de acero con la geometría mostrada. ¿Qué carga\(P\) puede soportar el marco sin ceder en ninguno de los elementos?

Ejercicio\(\PageIndex{16}\)

Un marco de truss de tres elementos está construido de acero con la geometría mostrada. ¿Qué carga\(P\) puede soportar el marco antes de que los tres elementos hayan cedido?

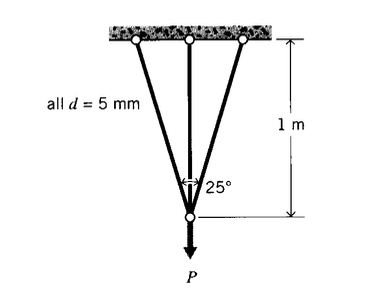
Ejercicio\(\PageIndex{17}\)

Si el marco del problema anterior se carga hasta que los tres miembros hayan cedido y la carga luego se reduzca a cero, encuentre la tensión residual en el elemento central.

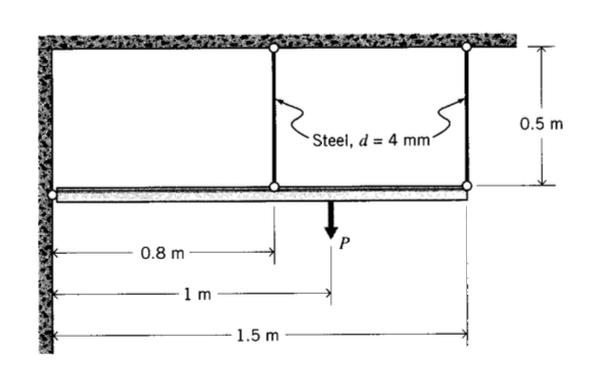
Ejercicio\(\PageIndex{18}\)

Una viga rígida está articulada en un extremo como se muestra y soportada por dos varillas verticales como se muestra.

a) ¿Qué carga\(P\) puede soportar la estructura antes de que ambas barras verticales hayan cedido?
b) ¿Cuál es la tensión residual en las barras verticales después de que la carga se haya reducido a cero?

Ejercicio\(\PageIndex{19}\)

Estimar la fuerza de estirado requerida para reducir el diámetro de una varilla de\(0.125''\) aluminio en un 50% en una operación de trefilado de alambre.