6.4: Introducción a la mecánica de fracturas

Introducción

En 1983, la Oficina Nacional de Estándares (ahora el Instituto Nacional de Ciencia y Tecnología) y Battelle Memorial Institute (R.P. Reed et al., NBS Special Publication 647-1, Washington, 1983.) estimaron que los costos por falla por fractura fueron de 119 mil millones de dólares anuales en dólares de 1982. Los dólares son importantes, pero el costo de muchos fracasos en la vida humana y lesiones lo es infinitamente más.

Las fallas se han producido por muchas razones, incluyendo incertidumbres en la carga o el ambiente, defectos en los materiales, insuficiencias en el diseño y deficiencias en la construcción o mantenimiento. El diseño contra fractura tiene una tecnología propia, y esta es un área muy activa de investigación actual. Este módulo brindará una introducción a un aspecto importante de este campo, ya que sin una comprensión de la fractura los métodos en el análisis de esfuerzos discutidos anteriormente serían de poca utilidad. Nos centraremos en las fracturas debido al simple sobreesfuerzo de tracción, pero nuevamente se advierte al diseñador sobre la necesidad de considerar absolutamente tantos factores como sea posible que puedan conducir al fracaso, especialmente cuando la vida está en riesgo.

El módulo sobre la base de dislocación de rendimiento (Módulo 21) muestra cómo la resistencia de los metales estructurales, particularmente el acero, se puede aumentar a niveles muy altos mediante la manipulación de la microestructura para inhibir el movimiento de dislocación. Desafortunadamente, esto hace que el material se vuelva quebradizo, de manera que las grietas se pueden formar y propagar catastróficamente con muy poca advertencia. Un número desafortunado de desastres de ingeniería están relacionados directamente con este fenómeno, y los ingenieros involucrados en el diseño estructural deben estar al tanto de los procedimientos disponibles ahora para salvaguardar contra la fractura quebradiza.

La dificultad central en el diseño contra la fractura en materiales de alta resistencia es que la presencia de grietas puede modificar las tensiones locales hasta tal punto que los análisis de tensión elástica realizados tan cuidadosamente por los diseñadores son insuficientes. Cuando una grieta alcanza cierta longitud crítica, puede propagarse catastróficamente a través de la estructura, aunque el esfuerzo bruto es mucho menor de lo que normalmente causaría rendimiento o falla en una muestra de tracción. El término “mecánica de fractura” se refiere a una especialización vital dentro de la mecánica de sólidos en la que se asume la presencia de una grieta, y deseamos encontrar relaciones cuantitativas entre la longitud de la grieta, la resistencia inherente del material al crecimiento de la grieta y la tensión a la que la grieta se propaga a alta velocidad para causar falla estructural.

El enfoque del balance energético

Cuando A.A. Griffith (1893—1963) comenzó sus estudios pioneros de fractura en vidrio en los años previos a 1920, estaba al tanto del trabajo de Inglis en el cálculo de las concentraciones de tensión alrededor de agujeros elípticos, y naturalmente consideró cómo podría ser utilizada en el desarrollo de un enfoque fundamental para predecir fracturas fortalezas. Sin embargo, la solución Inglis plantea una dificultad matemática: en el límite de una grieta perfectamente aguda, las tensiones se acercan al infinito en la punta de la grieta. Esto es obviamente no físico (en realidad el material generalmente experimenta alguna deformación local para despuntar la punta de la grieta), y usar tal resultado predeciría que los materiales tendrían una resistencia cercana a cero: incluso para cargas aplicadas muy pequeñas, las tensiones cerca de las puntas de la grieta se volverían infinitas, y las uniones allí serían ruptura. En lugar de centrarse directamente en las tensiones de la punta de la grieta, Griffith empleó un enfoque de balance energético que se ha convertido en uno de los desarrollos más famosos de la ciencia de los materiales (A.A. Griffith, Philosophical Transactions, Serie A, Vol. 221, pp. 163—198, 1920. La importancia del trabajo de Griffith en fractura no se reconoció en gran medida hasta la década de 1950. Véase J.E. Gordon, The Science of Structures and Materials, Scientific American Library, 1988, para un relato personal de la historia de Griffith.).

La energía de deformación por unidad de volumen de material estresado es

\(U^* = \dfrac{1}{V} \int f\ dx = \int \dfrac{f}{A} \dfrac{dx}{L} =\int \sigma d\epsilon\)

Si el material es lineal (\(\sigma = E_{\epsilon}\)), entonces la energía de deformación por unidad de volumen es

\(U^* = \dfrac{E_{\epsilon}^2}{2} = \dfrac{\sigma^2}{2E}\)

Cuando una grieta se ha convertido en un sólido a una profundidad\(a\), se descarga una región de material adyacente a las superficies libres y se libera su energía de deformación. Usando la solución Inglis, Griffith pudo calcular cuánta energía es esta.

Figura 1: Idealización de la región descargada cerca de los flancos de la grieta.

Una manera sencilla de visualizar esta liberación de energía, ilustrada en la Figura 1, es considerar dos regiones triangulares cercanas a los flancos de la grieta, de anchura\(a\) y altura\(\beta_a\), como completamente descargadas, mientras que el material restante sigue sintiendo la tensión total\(\sigma\). El parámetro se\(\beta\) puede seleccionar de manera que esté de acuerdo con la solución Inglis, y resulta que para la carga de tensión plana\(\beta = \pi\). La energía de deformación total\(U\) liberada es entonces la energía de deformación por unidad de volumen multiplicada por el volumen en ambas regiones triangulares:

\(U = -\dfrac{\sigma^2}{2E} \cdot \pi a^2\)

Aquí la dimensión normal al\(x-y\) plano se toma como unidad, así\(U\) es la energía de deformación liberada por unidad de espesor de la muestra. Esta energía de cepa es liberada por el crecimiento de grietas. Pero al formar la grieta, los enlaces deben romperse, y la energía de unión requerida es en efecto absorbida por el material. La energía superficial\(S\) asociada con una grieta de longitud\(a\) (y profundidad unitaria) es:

\(S = 2 \gamma a\)

donde\(\gamma\) está la energía superficial (e.g., Julios/metro\(^2\)) y el factor 2 es necesario ya que se han formado dos superficies libres. Como se muestra en la Figura 2, la energía total asociada con la grieta es entonces la suma de la energía (positiva) absorbida para crear las nuevas superficies, más la energía de deformación (negativa) liberada al permitir que las regiones cercanas a los flancos de la grieta se descarguen.

Figura 2: El balance energético de la fractura.

A medida que la grieta se alarga (\(a\)aumenta), la dependencia cuadrática de la energía de deformación en un tiempo domina la energía superficial, y más allá de una longitud crítica de la grieta ac, el sistema puede disminuir su energía al dejar que la grieta crezca aún más tiempo. Hasta el punto donde\(a = a_c\), la grieta crecerá sólo si el estrés en aumento. Más allá de ese punto, el crecimiento del crack es espontáneo y catastrófico

El valor de la longitud crítica de la grieta se puede encontrar estableciendo la derivada de la energía\(S+U\) total en cero:

Dado que la fractura rápida es inminente cuando se satisface esta condición, escribimos el estrés como\(\sigma_f\). Resolviendo,

\(\sigma_f = \sqrt{\dfrac{2E_{\gamma}}{\pi a}}\)

La obra original de Griffith se refería a materiales muy quebradizos, específicamente varillas de vidrio. Cuando el material exhibe más ductilidad, la consideración de la energía superficial por sí sola no proporciona un modelo preciso para la fractura. Esta deficiencia fue posteriormente remediada, al menos en parte, independientemente por Irwin (G.R. Irwin, “Fracture Dynamics”, Fracturing of Metals, American Society for Metals, Cleveland, 1948.) y Orowan (E. Orowan, “Fracture and Strength of Solids,” Report of Progress in Physics, Vol. 12, 1949.). Sugirieron que en un material dúctil una buena parte —de hecho la gran mayoría— de la energía de deformación liberada se absorbió no creando nuevas superficies, sino por la disipación de energía debido al flujo de plástico en el material cerca de la punta de la grieta. Sugirieron que la fractura catastrófica ocurre cuando la energía de deformación se libera a una velocidad suficiente para satisfacer las necesidades de todos estos “sumideros” de energía, y denotaron esta tasa crítica de liberación de energía de deformación por el parámetro\(\mathcal{G}_c\); la ecuación de Griffith puede entonces reescribirse en la forma:

\[\sigma_f = \sqrt{\dfrac{E\mathcal{G}_c}{\pi a}}\]

Esta expresión describe, de manera muy sucinta, la interrelación entre tres aspectos importantes del proceso de fractura: el material, como se evidencia en la tasa crítica de liberación de energía de deformación\(\mathcal{G}_c\); el nivel de esfuerzo\(\sigma_f\); y el tamaño\(a\),, de la falla. En una situación de diseño, uno podría elegir un valor de a basado en la grieta más pequeña que podría detectarse fácilmente. Entonces, para un material dado con su valor asociado de\(\mathcal{G}_c\), se\(\sigma_f\) podría determinar el nivel seguro de estrés. La estructura sería entonces dimensionada para mantener el estrés de trabajo cómodamente por debajo de este valor crítico.

Ejemplo\(\PageIndex{1}\)

La historia del avión DeHavilland Comet de principios de la década de 1950, en el que al menos dos aviones se desintegraron en vuelo, proporciona una visión trágica pero fascinante de la importancia de la teoría de fracturas. También es una historia espeluznante, habiendo sido casi predicha en una novela de 1948 de Nevil Shute llamada No Highway. El libro más tarde se convirtió en una película protagonizada por James Stewart como un metalúrgico perserverante convencido de que el nuevo avión de su compañía (el “Reno”) era fatalmente propenso a la fatiga del metal. Cuando apenas unos años después el Cometa estaba determinado a tener casi exactamente este problema, tanto el libro como la película se hicieron bastante famosos en la comunidad de ingeniería de materiales.

El estudio post mortem de los problemas del cometa fue uno de los más extensos en la historia de la ingeniería (T. Bishop, Metal Progress, Vol. 67, pp. 79—85, mayo de 1955.). Exigió rescatar casi toda la aeronave de los restos dispersos en el fondo del océano y también implicó la presurización a gran escala de una aeronave en un tanque de agua gigante. Si bien se aprendieron valiosas lecciones, es difícil exagerar el daño causado a la Compañía DeHaviland y a la industria aeronáutica británica en general. A veces se argumenta que el largo predominio de Estados Unidos en los aviones comerciales se debe al menos en parte a la desgracia del Cometa.

El avión Comet tenía un fuselaje de aluminio revestido, con\(\mathcal{G}_c \approx 300\) in-psi. El esfuerzo circular debido a la presurización relativa de la cabina fue de 20,000 psi, y a esa tensión la longitud de la grieta que se propagará catastróficamente es

\[a = \dfrac{\mathcal{G}_c E}{\pi \sigma^2} = \dfrac{(300)(11 \times 10^6)}{\pi (20 \times 10^3)^2} = 2.62'' \nonumber\]

Presumiblemente se detectaría una grieta en la inspección de rutina mucho antes de que pudiera crecer a esta longitud. Pero en el caso del Cometa, las grietas se propagaban desde los agujeros de los remaches cercanos a las ventanas de la cabina. Cuando la grieta llegó a la ventana, el tamaño de la abertura de la ventana se agregó efectivamente a la longitud de la grieta, lo que provocó un desastre.

Los aviones modernos se construyen con este modo de falla en mente, y tienen “tiras de rasgado” que supuestamente son capaces de detener cualquier grieta de rápido crecimiento. Pero este remedio no siempre es efectivo, como quedó demostrado en 1988 cuando un B737 operado por Aloha Airlines tenía el techo de la cabina de primera clase arrancado. Esa aeronave tuvo daños por corrosión bajo tensión en varios remaches en los empalmes de vuelta del fuselaje, y esto permitió que múltiples grietas pequeñas se unieran para formar una gran grieta. Actualmente se está prestando mucha atención a la protección contra este tipo de “daños multisitio”.

Figura\(\PageIndex{1}\): El fuselaje del vuelo 243 de Aloha Airlines tras explotar mientras estaba en vuelo el 28 de abril de 1988. (Dominio Público; Junta Nacional de Seguridad en el Transporte (NTSB) vía Wikipedia)

Es importante darse cuenta de que la longitud crítica de la grieta es un número absoluto, no dependiendo del tamaño de la estructura que la contiene. Cada vez que la grieta salta hacia adelante, digamos en un pequeño incremento\(\delta a\), se libera una cantidad adicional de energía de deformación del material recién descargado cerca de la grieta. Nuevamente usando nuestra imagen simplista de una región de forma triangular que se encuentra en tensión cero mientras el resto de la estructura continúa sintiendo el estrés general aplicado, es fácil ver en la Figura 3 que se libera mucha más energía debido al salto en la posición 2 que en la posición 1. Esta es otra razón más por la que las cosas pequeñas tienden a ser más fuertes: simplemente no son lo suficientemente grandes como para contener una grieta de longitud crítica.

Figura 3: Energía liberada durante un incremento del crecimiento de la grieta, para dos longitudes de grieta diferentes.

Ejemplo\(\PageIndex{2}\)

Gordon (J.E. Gordon, Structures, or Why Things Don't Fall Down, Plenum, New York, 1978.) habla del cocinero de un barco que un día notó una grieta en la cubierta de acero de su cocina. Sus superiores le aseguraron que no era nada de qué preocuparse —la grieta era ciertamente pequeña en comparación con el vasto grueso del barco— pero el cocinero comenzó a pintar fechas en el piso para marcar la nueva longitud de la grieta cada vez que un ataque de mal tiempo la haría crecer más. Con cada avance de la grieta, se descargó material adicional de tarima y se liberó la energía de deformación que anteriormente contenía. Pero a medida que la cantidad de energía liberada crece cuadráticamente con la longitud de la grieta, eventualmente hubo suficiente disponibilidad para mantener la grieta creciendo incluso sin ningún aumento adicional en la carga bruta. Cuando esto sucedió, el barco se rompió en dos pedazos; esto parece increíble pero hay más de unos pocos sucesos de este tipo que están muy bien documentados. Al igual que sucedió, se rescató la parte del barco con las marcas que muestran el crecimiento de la grieta, y esto se ha convertido en uno de los ejemplos mejor documentados de crecimiento lento de grietas seguido de una fractura catastrófica final.

Calibración de cumplimiento

Hay una serie de medios disponibles por los cuales se\(\mathcal{G}_c\) puede medir la propiedad del material. Uno de estos se conoce como calibración de cumplimiento, que emplea el concepto de cumplimiento como una relación de deformación a carga aplicada:\(C = \delta/P\). La energía de deformación total se\(U\) puede escribir en términos de este cumplimiento como:

\(U = \dfrac{1}{2} P \delta = \dfrac{1}{2} CP^2\)

Figura 4: Cumplimiento en función de la longitud de la grieta.

La conformidad de un espécimen adecuado, por ejemplo una viga en voladizo, podría medirse experimentalmente en función de la longitud a de una grieta que se cultiva en el espécimen (ver Figura 4. La velocidad de liberación de energía de deformación se puede determinar diferenciando la curva de cumplimiento frente a la longitud:

\[\mathcal{G} = \dfrac{\partial U}{\partial a} = \dfrac{1}{2} P^2 \dfrac{\partial C}{\partial a}\]

El valor crítico de\(\mathcal{G}\),\(\mathcal{G}_c\), se encuentra entonces midiendo la carga crítica\(P_c\) necesaria para fracturar una muestra que contiene una grieta de longitud\(a_c\), y utilizando la pendiente de la curva de cumplimiento a este mismo valor de\(a\):

\[\mathcal{G}_c = \dfrac{1}{2}P_c^2 \dfrac{\partial C}{\partial a} |_{a = a_c}\]

Ejemplo\(\PageIndex{3}\)

Figura 5: Espécimen de fractura de DCB.

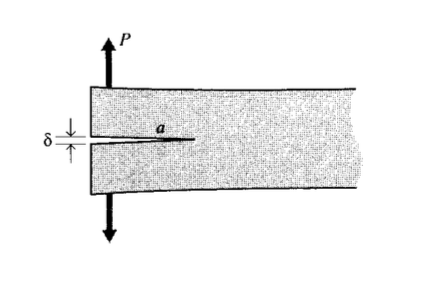
Para una muestra de viga de doble voladizo (DCB) como la que se muestra en la Figura 5, la teoría del haz da la deflexión como

\(\dfrac{\delta}{2} = \dfrac{Pa^3}{3EI}\)

donde\(I = bh^3/12\). El cumplimiento elástico es entonces

\(C = \dfrac{\delta}{P} = \dfrac{2a^3}{3EI}\)

Si se observa que la grieta salta hacia adelante cuando\(P = P_c\), la Ecuación 3 se puede usar para calcular la tasa de liberación de energía de deformación crítica como

\(\mathcal{G}_c = \dfrac{1}{2} P_c^2 \cdot \dfrac{2a^3}{EI} = \dfrac{12P_c^2 a^2}{b^2h^3E}\)

El enfoque de intensidad de estrés

Si bien el enfoque de balance energético proporciona una gran cantidad de conocimiento del proceso de fractura, un método alternativo que examina el estado de tensión cerca de la punta de una grieta afilada directamente ha demostrado ser más útil en la práctica de ingeniería. La literatura trata tres tipos de grietas, denominadas modo I, II y III como se ilustra en la Figura 6. El modo I es un modo de apertura normal y es el que enfatizaremos aquí, mientras que los modos II y III son modos de deslizamiento de cizallamiento. Como se esbozó en el Módulo 16, el método semi-inverso desarrollado por Westergaard muestra que las tensiones del modo de apertura son:

\[\begin{array} {c} {\sigma_x = \dfrac{K_I}{\sqrt{2\pi r}} \cos \dfrac{\theta}{2} (1 - \sin \dfrac{\theta}{2} \sin \dfrac{3 \theta}{2}) + \dots} \\ {\sigma_y = \dfrac{K_I}{\sqrt{2\pi r}} \cos \dfrac{\theta}{2} (1 + \sin \dfrac{\theta}{2} \sin \dfrac{3 \theta}{2}) + \dots} \\ {\tau_{xy} = \dfrac{K_I}{\sqrt{2\pi r}} \cos \dfrac{\theta}{2} \cos \dfrac{3\theta}{2} \sin \dfrac{\theta}{2} \cdots} \end{array}\]

Para distancias cercanas a la punta de la grieta\((r\le 0.1a)\), se pueden descuidar los términos de segundo y orden superior indicados por puntos. A grandes distancias de la punta de la grieta, estas relaciones dejan de aplicarse y las tensiones se acercan a sus valores de campo lejano que obtendrían si la grieta no estuviera presente.

Figura 6: Modos de fractura.

El\(KI\) en Eqns. 6.4.4 es un parámetro muy importante conocido como el factor de intensidad de estrés. El subíndice I se utiliza para denotar el modo de apertura de grieta, pero se aplican relaciones similares en los modos II y III. Las ecuaciones muestran tres factores que en conjunto representan el estado de tensión cerca de la punta de la grieta: el factor denominador\((2\pi r)^{-1/2}\) muestra la naturaleza singular de la distribución de tensiones; se\(\sigma\) acerca al infinito a medida que se acerca la punta de la grieta, con una\(r^{-1/2}\) dependencia. La dependencia angular es separable como otro factor: e.g\(f_x = \cos \theta/2 \cdot (1 - \sin \theta/2 \sin 3\theta/2) + \cdots\). El factor\(K_I\) contiene la dependencia de la tensión aplicada\(\sigma_{\infty}\), la longitud\(a\) de la grieta y la geometría de la muestra. El\(KI\) factor da la intensidad general de la distribución del estrés, de ahí su nombre.

Para el caso específico de una grieta central de ancho\(2a\) o una grieta de borde de longitud\(2a\) en una hoja grande\(K_I = \sigma_{\infty} \sqrt{\pi a}\), y\(K_I = 1.12 \sigma_{\infty} \sqrt{\pi a}\) para una grieta de borde de longitud\(2a\) en una hoja grande. (El factor obviamente\(\pi\) podría cancelarse con el\(\pi\) en el denominador de la Ecuación 6.4.4, pero comúnmente se conserva por coherencia con trabajos anteriores.) Las expresiones\(K_I\) para algunas geometrías adicionales se dan en la Tabla 1. La literatura contiene expresiones\(K\) para un gran número de geometrías de grieta y carga, y existen procedimientos tanto numéricos como experimentales para determinar el factor de intensidad de tensión es geometrías reales específicas.

Cuadro 1: Factores de intensidad de estrés para varias geometrías comunes.

Tipo de Grieta	Factor de Intensidad de Estrés\(K_I\)
Grieta central, longitud\(2a\), en una placa infinita	\(\sigma_{\infty} \sqrt{\pi a}\)
Grieta de borde\(a\), longitud, en una placa semi-infinita	\(1.12 \sigma_{\infty} \sqrt{\pi a}\)
Grieta central en forma de centavo, radio\(a\), en cuerpo infinito	\(2 \sigma_{\infty} \sqrt{\tfrac{a}{\pi}}\)
Grieta central, longitud\(2a\) en placa de ancho\(W\)	\(\sigma_{\infty} \sqrt{W \tan (\tfrac{\pi a}{W})}\)
2 fisuras simétricas de borde\(a\), cada longitud, en placa de ancho total\(W\)	\(\sigma_{\infty} \sqrt{W[\tan (\tfrac{\pi a}{W}) + 0.1 \sin (\dfrac{2 \pi a}{W})]}\)

Estos factores de intensidad de tensión se utilizan en el diseño y análisis argumentando que el material puede soportar tensiones de punta de grieta hasta un valor crítico de intensidad de tensión, denominado\(K_{Ic}\), más allá del cual la grieta se propaga rápidamente. Este factor crítico de intensidad de tensión es entonces una medida de la tenacidad del material. La tensión de falla\(\sigma_f\) se relaciona entonces con la longitud de la grieta a y la tenacidad a la fractura por

\[\sigma_f = \dfrac{K_{Ic}}{\alpha \sqrt{\pi a}}\]

donde\(\alpha\) es un parámetro geométrico igual a 1 para grietas de borde y generalmente en el orden de unidad para otras situaciones. Las expresiones para α se tabulan para una amplia variedad de geometrías de espécimen y grietas, y los métodos especiales de elementos finitos están disponibles para calcularlo para nuevas situaciones.

Los puntos de vista de intensidad de estrés y energía están interrelacionados, como se puede ver al comparar las ecuaciones 6.4.1 y 6.4.5 (con\(\alpha = 1\)):

\(\sigma_f = \sqrt{\dfrac{E\mathcal{G}_c}{\pi a}} = \dfrac{K_{Ic}}{\sqrt{\pi a}} \to K_{Ic}^2 = E \mathcal{G}_c\)

Esta relación se aplica en la tensión plana; es ligeramente diferente en la deformación plana:

Para metales con\(v = .3\),\((1 - v^2) = 0.91\). Esto no es un gran cambio; sin embargo, los valores numéricos de\(\mathcal{G}_c\) o\(K_{Ic}\) son muy diferentes en situaciones de tensión plana o deformación plana, como se describirá a continuación.

Los valores típicos de\(G_{Ic}\) y\(K_{Ic}\) para diversos materiales se enumeran en la Tabla 2, y se ve que varían en un rango muy amplio de material a material. Algunos polímeros pueden ser muy duros, especialmente cuando se clasifican en bases por libra, pero las aleaciones de acero son difíciles de batir en términos de resistencia absoluta a la propagación de grietas.

Cuadro 2: Tenacidad a la fractura de materiales.

Material	\(G_{Ic} (kJm^{-2})\)	\(K_{Ic}(MNm^2)\)	\(E(GPa)\)
Aleación de acero	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">107	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">150	\ (E (GPa)\)” class="lt-eng-44553">210
Aleación de aluminio	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">20	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">37	\ (E (GPa)\)” class="lt-eng-44553">69
Polietileno	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">20 (\(J_{Ic}\))	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">-	\ (E (GPa)\)” class="lt-eng-44553">0.15
Poliestireno de alto impacto	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">15.8 (\(J_{Ic}\))	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">-	\ (E (GPa)\)” class="lt-eng-44553">2.1
Acero - suave	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">12	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">50	\ (E (GPa)\)” class="lt-eng-44553">210
Caucho	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">13	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">-	\ (E (GPa)\)” class="lt-eng-44553">0.001
Termoestable reforzado con vidrio	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">7	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">7	\ (E (GPa)\)” class="lt-eng-44553">7
Epoxi endurecido con caucho	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">2	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">2.2	\ (E (GPa)\)” class="lt-eng-44553">2.4
PMMA	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">0.5	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">1.1	\ (E (GPa)\)” class="lt-eng-44553">2.5
Poliestireno	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">0.4	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">1.1	\ (E (GPa)\)” class="lt-eng-44553">3
Madera	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">0.12	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">0.5	\ (E (GPa)\)” class="lt-eng-44553">2.1
Vidrio	\ (G_ {Ic} (kjM^ {-2})\)” class="lt-eng-44553">0.007	\ (K_ {Ic} (MnM^2)\)” class="lt-eng-44553">0.7	\ (E (GPa)\)” class="lt-eng-44553">70

Ejemplo\(\PageIndex{4}\)

La ecuación 6.4.5 proporciona una relación de diseño entre la tensión aplicada\(\sigma\), la tenacidad\(K_{Ic}\) del material y la longitud de la grieta\(a\). Cualquiera de estos parámetros se puede calcular una vez que se conocen los otros dos. Para ilustrar una aplicación del proceso, digamos que deseamos determinar la presión de operación segura en un recipiente a presión de aluminio de 0.25 m de diámetro y con un espesor de pared de 5 mm. Primero asumiendo falla por rendimiento cuando el esfuerzo circular alcanza el límite elástico (330 MPa) y usando un factor de seguridad de 0.75, podemos calcular la presión máxima como

\(p = \dfrac{0.75 \sigma t}{r} = \dfrac{0.75 \times 330 \times 10^6}{0.25/2} = 9.9\text{ MPa} = 1400\text{ psi}\)

Para asegurar contra fallas mediante un rápido crecimiento de grietas, ahora calculamos la longitud máxima de grieta permisible a la tensión de operación, utilizando un valor de tenacidad de\(K_{Ic} = 41 \text{ MPa} \sqrt{m}\):

\(a = \dfrac{K_{Ic}^2}{\pi \sigma^2} = \dfrac{(41 \times 10^6)^2}{\pi (0.75 \times 330 \times 10^6)^2} = 0.01\ m = 0.4\ in\)

Aquí se\(\alpha = 1\) ha asumido una grieta de borde con. Se debe implementar un cronograma de inspección que sea capaz de detectar grietas antes de que alcancen este tamaño.

Efecto de la geometría de la muestra

Figura 7: Tensión limitada por el rendimiento dentro de la zona\(r_p\).

La tenacidad, o resistencia al crecimiento de grietas, de un material se rige por la energía absorbida a medida que la grieta avanza. En un material extremadamente quebradizo como el vidrio de ventana, esta energía es principalmente la de romper los enlaces químicos a lo largo del plano de la grieta. Pero como ya se mencionó, en materiales más duros, la ruptura de la unión juega un papel relativamente pequeño en la resistencia al crecimiento de grietas, con mucho, la mayor parte de la energía de fractura se asocia con el flujo de plástico cerca de la punta de la grieta. Una “zona plástica” está presente cerca de la punta de la grieta dentro de la cual las tensiones predichas por la Ecuación 6.4.4 estarían por encima del límite elástico del material\(\sigma_Y\). Dado que el estrés no puede elevarse por encima\(\sigma_Y\), el estrés en esta zona es\(\sigma_Y\) más que el que da la Ecuación 6.4.4. A una primera aproximación, la distancia rp que esta zona se extiende a lo largo del\(x\) eje se puede encontrar usando la Ecuación 6.4.4 con\(\theta = 0\) para encontrar la distancia a la que la tensión de la punta de la grieta se reduce a\(\sigma_Y\):

\(\sigma_y = \sigma_Y = \dfrac{K_I}{\sqrt{2\pi r_p}}\)

\[r_p = \dfrac{K_I^2}{2 \pi \sigma_Y^2\]

Esta relación se ilustra en la Figura 7. A medida que aumenta la intensidad de tensión ya sea elevando la tensión impuesta o por el alargamiento de la grieta, el tamaño de la zona plástica también aumentará. Pero la extensión del flujo plástico está finalmente limitada por la movilidad molecular o microestructural del material, y la zona puede llegar a ser tan grande. Cuando la zona no puede crecer, la grieta ya no puede restringirse y se produce una propagación inestable. El valor\(K_I\) al que esto ocurre puede entonces considerarse una propiedad de materiales, nombrada\(K_{Ic}\).

Para que el valor medido de\(K_{Ic}\) sea válido, el tamaño de la zona plástica no debe ser tan grande como para interactuar con los límites libres del espécimen o para destruir la naturaleza básica de la distribución de tensión singular. La especificación ASTM para pruebas de tenacidad a la fractura (E 399-83, “Método de prueba estándar para la tenacidad a la fractura por deformación plana de materiales metálicos”, ASTM, 1983.) especifica la geometría de la muestra para asegurar que la muestra es grande en comparación con la longitud de la grieta y el tamaño de la zona plástica (ver Figura 8):

Figura 8: Dimensiones de la muestra de tenacidad a la fractura.

Se ha prestado mucha atención al importante caso en el que existe suficiente ductilidad para que sea imposible satisfacer los criterios anteriores. En estos casos se debe abandonar la vista de intensidad de tensión y utilizar en su lugar técnicas alternativas como la integral J o el método de desplazamiento de apertura de la punta de la grieta. Se remite al lector a las referencias listadas al final del módulo para la discusión de estos enfoques.

Figura 9: Efecto del espesor de la muestra sobre la tenacidad.

La tenacidad a la fractura medida por\(K_c\) o\(\mathcal{G}_c\) es esencialmente una medida de la extensión de la deformación plástica asociada con la extensión de la grieta. Se esperaría que la cantidad de flujo de plástico escalara linealmente con el grosor de la muestra, ya que reducir el grosor a la mitad cortaría naturalmente el volumen de material plásticamente deformado aproximadamente a la mitad también. Por lo tanto, la tenacidad se eleva linealmente, al menos inicialmente, con el espesor de la muestra como se ve en la Figura 9. Eventualmente, sin embargo, se observa que la tenacidad pasa por un máximo y luego cae a un valor menor. Esta pérdida de tenacidad más allá de un cierto espesor crítico\(t^*\) es extremadamente importante en el diseño contra la fractura, ya que el uso de una muestra demasiado delgada en la medición de la tenacidad dará un valor poco realista optimista para\(\mathcal{G}_C\). Los requisitos de tamaño de la muestra para pruebas válidas de tenacidad a la fractura son tales que se mide el valor más conservador.

El espesor crítico es aquel que provoca que el espécimen esté dominado por un estado de deformación plana, a diferencia de la tensión plana. La tensión en la\(z\) dirección a través del espesor debe llegar a ser cero en los lados de la muestra ya que no se aplica tracción allí, y en una muestra delgada la tensión no tendrá espacio para elevarse a valores apreciables dentro del material. La deformación en la\(z\) dirección no es cero, por supuesto, y el espécimen experimentará una contracción de Poisson dada por\(\epsilon_z = v(\sigma_x + \sigma_y)\). Pero cuando el espécimen es más grueso, el material cerca del centro no podrá contraerse lateralmente debido a la restricción del material adyacente. Ahora la deformación\(z\) -dirección es cero, por lo que surgirá una tensión de tracción a medida que el material intente contraerse pero se le impide hacerlo. El valor de σz se eleva desde cero en la superficie exterior y se aproxima a un valor máximo dado por\(\sigma_z \approx v(\sigma_x + \sigma_y)\) en una distancia\(t^*\) como se ve en la Figura 10. Para garantizar que dominen las condiciones de deformación plana, el espesor de la muestra\(t\) debe ser tal que\(t \gg 2t^*\).

El estado de tensión triaxial establecido cerca del centro de un espécimen grueso cerca de la punta de la grieta reduce el esfuerzo cortante máximo disponible para impulsar el flujo de plástico, ya que el esfuerzo cortante máximo es igual a la mitad de la diferencia de la tensión principal más grande y menor, y el más pequeño ahora es mayor que cero. O equivalentemente, podemos afirmar que la movilidad del material se ve limitada por la incapacidad de contraerse lateralmente. Ya sea desde el punto de vista de tensión o deformación, la extensión de la plasticidad disponible se reduce haciendo que la muestra sea gruesa.

Ejemplo\(\PageIndex{5}\)

Los tamaños de zona plástica para los casos de tensión plana y deformación plana se pueden visualizar usando un criterio de rendimiento adecuado junto con las expresiones de tensión cerca de la punta de la grieta. El criterio de rendimiento v. Mises se dio en términos de tensiones principales en el Módulo 20 como

Las tensiones principales se pueden obtener de Eqns. 6.4.4 como

\(\sigma_1 = \dfrac{K_I}{\sqrt{2 \pi r}} \cos \dfrac{\theta}{2} (1 + \sin \dfrac{\theta}{2})\)

El tercer estrés principal es

\(\sigma_3 = \begin{cases} 0, \text{ plane stress} \\ v(\sigma_1 + \sigma_2), \text{ plane strain} \end{cases}\)

Estas tensiones pueden sustituirse en el criterio de rendimiento, que luego se resuelve para el radio\(r\) en el que se produce el rendimiento. Es conveniente normalizar este radio por los raduis de la zona plástica a lo largo del\(x\) eje −, dado por la Ecuación 6.4.6. Los comandos de Maple para llevar a cabo estas sustituciones y trazar el resultado son:

# Radio de la zona plástica a lo largo del eje x > rp: =K [I] ^2/ (2*PI*Sigma [Y] ^2):

# v. Criterio de rendimiento Mises en términos de tensiones principales
> v_mises: =2*sigma [Y] ^2= (sigma [1] -sigma [2]) ^2 + (sigma [1] -sigma [3]) ^2 + (sigma [2] -sigma [3]) ^2:

# Tensiones principales en la región de la punta de la grieta
> sigma [1]: =( K [I] /sqrt (2*pi*r)) *cos (theta/2) * (1+sin (theta/2)):
> sigma [2]: =( K [I] /sqrt (2*pi*r)) *cos (theta/2) * (1-sin (theta/2));

# Evaluar v. Mises para tensión plana (v_strs) y deformación plana (v_strn) # Toma nu = 0.3
> v_strs: =subs (sigma [3] =0, v_mises):
> v_strn: =subs (sigma [3] =.3* (sigma [1] +sigma [2]), v_mises):

# Resuelve para radio de zona plástica, normaliza por rp
# pl_strs para caso de tensión plana, pl_strn para deformación plana > pl_strs: =solve (v_strs, r) /rp:
> pl_strn: =solve (v_strn, r) /rp:

# Trazar zonas plásticas normalizadas para tensión plana y deformación plana > plot ({pl_strs, pl_strn}, theta=0.. 2*Pi, coords=polar);

Figura 11: Formas de zonas plásticas normalizadas para deformación plana (contorno interno) y tensión plana (contorno exterior).

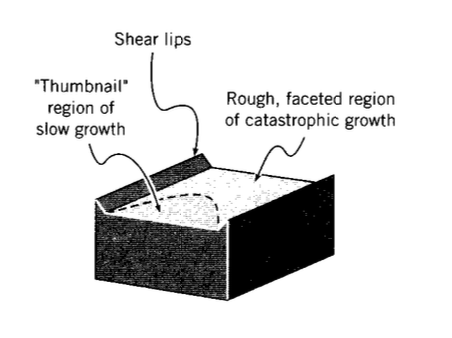
Incluso en una muestra gruesa, la tensión en la dirección z debe acercarse a cero en las superficies laterales. Por lo tanto, las regiones cercanas a la superficie están libres de la restricción de tensión triaxial y presentan un mayor flujo de plástico impulsado por cizallamiento. Después de que un espécimen agrietado haya sido probado hasta el fracaso, a menudo será visible un patrón plano de “miniatura” como se ilustra en la Figura 12. Esta es la región de crecimiento lento de la grieta, donde la grieta es capaz de mantener su orientación preferida transversal a la tensión en la dirección y. El crecimiento de grietas cerca de los bordes es retardado por el flujo de plástico adicional allí, por lo que la línea de grieta se inclina hacia adentro Cuando la tensión se incrementa lo suficiente como para hacer que la grieta crezca catastróficamente, normalmente lo hace a velocidades lo suficientemente altas como para que la orientación transversal no siempre se mantenga. La región de fractura rápida es así facetada y rugosa, lo que lleva a algunos mecánicos de traspatio a reclamar que el material falló porque “cristalizó”.

A lo largo de los bordes de la muestra, a menudo se pueden encontrar “labios de corte” en los que la grieta se ha desarrollado por flujo de cizallamiento y con deformación plástica intensiva. Los labios estarán cerca de un\(^{\circ}\) ángulo de 45, la orientación de los planos de corte máximo.

Tamaño y temperatura del grano

Figura 12: Topografía superficial de fractura.

El acero es un material estructural tan importante y ampliamente utilizado que es fácil olvidar que el acero es una innovación tecnológica bastante reciente. Bien entrado el siglo XIX, la madera era el material dominante para muchos puentes, edificios y barcos. A medida que el uso del hierro y el acero se generalizaron en la última parte de ese siglo y en la primera parte del presente, se produjeron una serie de desastres que se pueden rastrear hasta el estado entonces incompleto de comprensión de estos materiales, especialmente en lo que respecta a su tendencia a volverse quebradizos a bajas temperaturas. Muchas de estas fallas han sido descritas y analizadas en un fascinante libro de Parker (E.R. Parker, Brittle Behavior of Engineering Structures, John Wiley & Sons, 1957.).

Uno de estos fracasos quebradizos es quizás el desastre más famoso de los últimos siglos, el hundimiento del transatlántico Titanic el 15 de abril de 1912, con una pérdida de unas mil 500 personas y sólo 705 sobrevivientes. Hasta hace muy poco, se pensaba que la tragedia era causada por un largo corte desgarrado en el casco del barco por un iceberg. Sin embargo, cuando finalmente se descubrieron los restos del barco en 1985 utilizando robots submarinos, no se encontró evidencia de tal corte. Además, los robots pudieron posteriormente devolver muestras del acero del barco cuyo análisis ha dado lugar a una explicación alternativa.

Ahora es bien sabido que los grados menores de acero, especialmente aquellos que tienen grandes concentraciones de impurezas como las inclusiones intersticiales de carbono, están sujetos a fragilización a bajas temperaturas. William Garzke, arquitecto naval de la firma neoyorquina de Gibbs & Cox, y sus colegas han argumentado que el acero en el Titanic era efectivamente quebradizo en las 31\(^{\circ}F\) aguas del Atlántico esa noche, y que la colisión de 22 nudos con el iceberg generó no un corte sino un extenso agrietamiento qué agua podría entrar en el casco. Si el acero hubiera permanecido duro a esta temperatura, estos autores sienten, el agrietamiento puede haber sido mucho menos extenso. Esto habría ralentizado las inundaciones y dado más tiempo para que las embarcaciones de rescate llegaran al lugar de los hechos, lo que podría haber incrementado mucho el número de supervivientes.

Figura 13: Apilamiento de dislocación dentro de un grano.

En los metales de transición bcc como el hierro y el acero al carbono, la falla quebradiza se puede iniciar por deslizamiento de dislocación dentro de un grano cristalino. El deslizamiento tiene lugar en el límite de fluencia\(\sigma_Y\), el cual varía con el tamaño de grano de acuerdo con la ley Hall-Petch como se describe en el Módulo 21:

\(\sigma_Y = \sigma_0 + k_Y d^{-1/2}\)

Las dislocaciones no son capaces de propagarse más allá de los límites del grano, ya que los granos adyacentes en general no tendrán sus planos de deslizamiento adecuadamente orientados. Las dislocaciones entonces se “amontonan” contra los límites de grano como se ilustra en la Figura 13. El pileup de dislocación actúa de manera similar a una grieta interna con una longitud que escala con el tamaño de grano d, intensificando la tensión en los granos circundantes. Sustituyendo a by\(d\) en la ecuación de Griffith modificada (Ecuación 6.4.1), la tensión aplicada necesaria para causar fractura en granos adyacentes se relaciona con el tamaño de grano como

\(\sigma_f = k_f d^{-1/2}, k_f \propto \sqrt{\dfrac{E\mathcal{G}_c}{\pi}}\)

Las dos relaciones anteriores para el rendimiento y la fractura se trazan en la Figura 14 frente al tamaño inverso del grano de la raíz (por lo que el tamaño de grano aumenta a la izquierda), siendo las pendientes\(k_Y\) y\(k_f\) respectivamente. Cuando\(k_f > k_Y\), la fractura no ocurrirá hasta\(\sigma = \sigma_Y\) para valores de d a la izquierda del punto\(A\), ya que el rendimiento y el deslizamiento es un requisito previo para la escisión. En esta región los esfuerzos de deformación y fractura son los mismos, y la falla parece quebradiza ya que el rendimiento a gran escala no tendrá oportunidad de ocurrir. A la derecha del punto\(A\), el cedimiento tiene lugar previo a la fractura y el material aparece dúctil. \(A\)Por lo tanto, el punto define un tamaño de grano crítico\(d^*\) en el que se llevará a cabo una transición de “nil-ductilidad” de dúctil (granos más pequeños que\(d^*\)) a falla quebradiza.

Figura 14: Efecto del tamaño de grano sobre el rendimiento y la tensión de fractura.

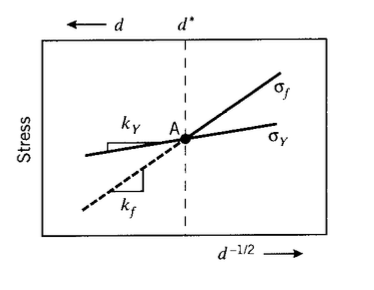
A medida que se baja la temperatura, el límite elástico σY aumentará como se describe en el Módulo 20, y el esfuerzo de fractura σf disminuirá (ya que la movilidad atómica y por lo tanto\(\mathcal{G}_C\) disminuirá). Por lo tanto, el punto\(A\) cambia hacia la derecha a medida que se baja la temperatura. El tamaño de grano crítico para la ductilidad nula ahora ocurre a un valor menor; es decir, los granos deben ser más pequeños para evitar fragilizar el material. Equivalentemente, refinar el tamaño de grano tiene el efecto de disminuir la temperatura de transición dúctil-quebradiza. Por lo tanto, el refinamiento del tamaño de grano aumenta tanto el rendimiento como el esfuerzo de fractura, disminuye la temperatura de transición dúctil-quebradiza y promueve la tenacidad también. Este es un mecanismo de fortalecimiento singularmente útil, ya que otras técnicas como el endurecimiento por deformación y el endurecimiento en solución sólida tienden a lograr el fortalecimiento a expensas de la tenacidad.

Factores distintos a la temperatura también pueden fragizar el acero. Inclusiones como carbono y fósforo actúan para inmovilizar sistemas de deslizamiento que de otro modo podrían aliviar las tensiones asociadas con los pileups de dislocación, y estas inclusiones pueden elevar el límite elástico y, por lo tanto, la temperatura de transición dúctil-quebradiza marcadamente. Efectos similares pueden ser inducidos por el daño de la radiación de alta energía, por lo que la fragilidad de los componentes del reactor nuclear es motivo de gran preocupación. La fragilización también se ve facilitada por la presencia de muescas, ya que generan tensiones triaxiales que restringen el flujo plástico. Las altas tasas de deformación promueven la fragilidad porque la tensión de flujo necesaria para acomodar la tasa de deformación es mayor, y la soldadura inadecuada puede conducir a fragilidad tanto alterando la microestructura del acero como generando tensiones internas residuales.

Referencias Generales

1. Anderson, T.L., Mecánica de Fracturas: Fundamentos y Aplicaciones, CRC Press, Boca Raton, 1991.

2. Barsom, J.M., ed., Fracture Mechanics Retrospective, American Society for Testing and Materials, Filadelfia, 1987.

3. Collins, J.A., Fallo de materiales en el diseño mecánico, Wiley, 1981.

4. Courtney, T.H., Comportamiento mecánico de materiales, McGraw-Hill, Nueva York, 1990.

5. Gordon, J.E., La nueva ciencia de los materiales fuertes, o por qué no te caes por el suelo, Princeton University Press, 1976.

6. Hertzberg, R.W., Mecánica de Deformación y Fractura de Materiales de Ingeniería, Wiley, Nueva York, 1976.

7. Knott, J.F., Fundamentos de la mecánica de fracturas, John Wiley — Halsted Press, Nueva York, 1973.

8. Mendenhall, W., R.L. Scheaffer y D.D. Wackerly, Estadística matemática con Applica- ciones, Duxbury Press, Boston, 1986.

9. Strawley, J.E., y W.F. Brown, Ensayo de Dureza a Fractura, ASTM STP 381, 133, 1965.

10. 1967.

Ejercicio\(\PageIndex{1}\)

Utilizando un desarrollo análogo al empleado en el Módulo 21 para el límite elástico teórico, muestran que la resistencia a la tracción teórica es\(\sigma^{th} \approx E/10\) (mucho mayor que la observada experimentalmente). Asumir una función de fuerza atómica armónica\(\sigma = \sigma^{th} \sin(2\pi x/\lambda\)), donde\(x\) está el desplazamiento de un átomo desde su posición de equilibrio y\(\lambda \approx a_0\) es el espaciamiento interatómico. El estrés máximo se\(\sigma^{th}\) puede encontrar usando

\(E = (\dfrac{d \sigma}{d\epsilon})_{x \to 0} \text{ and } \epsilon = \dfrac{x}{a_0}\)

Ejercicio\(\PageIndex{2}\)

Usando un factor de seguridad de 2, encuentre la presión de operación segura en un recipiente a presión de acero de extremo cerrado\(1'\) en diámetro y grosor de\(0.2''\) pared.

Ejercicio\(\PageIndex{3}\)

Se construye un recipiente a presión con un diámetro de\(d = 18''\) y una longitud de\(L = 6'\). El recipiente debe ser capaz de soportar una presión interna de\(p = 1000\text{ psi}\), y el espesor de la pared es tal que mantenga bajo la tensión nominal del aro\(2500\text{ psi}\). Sin embargo, el vaso estalla a una presión interna de solo\(500\text{ psi}\), y una investigación micrográfica revela que la fractura fue iniciada por una grieta interna\(0.1''\) de longitud. Calcular la tenacidad a la fractura (\(K_{Ic}\)) del material.

Ejercicio\(\PageIndex{4}\)

Una resina epoxi altamente reticulada tiene un coeficiente de expansión térmica lineal\(\alpha = 5 \times 10^{-5} K^{-1}\),\(G_{IC} = 120 J/m^2\),\(E = 3.2 GPa\), y\(v = 0.35\). Una capa gruesa de resina se cura y está firmemente unida a una pieza de aluminio (\(\alpha = 2.5 \times 10^{-5} K^{-1}\)) en\(180^{\circ} C\). Calcule el tamaño mínimo del defecto necesario para iniciar el agrietamiento en la resina al enfriarse a\(20^{\circ} C\). Tome\(\alpha\) en la Ecuación 6.4.5 para ser\(2/\pi\) para grietas en forma de centavo de radio\(a\) en una hoja ancha.

Ejercicio\(\PageIndex{5}\)

(a) Una placa gruesa de aleación de aluminio, de 175 mm de ancho, contiene una grieta ubicada centralmente de 75 mm de longitud. La placa experimenta fractura quebradiza a una tensión aplicada (uniaxial, transversal a la grieta) de 110 MPa. Determinar la tenacidad a la fractura del material.

b) ¿Cuál sería el esfuerzo de fractura si la placa fuera lo suficientemente ancha como para permitir una asunción de ancho infinito?

Ejercicio\(\PageIndex{6}\)

Para obtener durezas válidas de fractura por deformación plana, el tamaño de la zona plástica debe ser pequeño con respecto al grosor de la muestra\(B\), la longitud\(a\) de la grieta y el ancho del “ligamento”\(W - a\). El criterio establecido es

Clasificar los materiales en la base de datos en términos del parámetro dado en el lado derecho de esta expresión.

Ejercicio\(\PageIndex{7}\)

Cuando se aplica una carga de 150 kN a una muestra de tracción que contiene una grieta de 35 mm, el desplazamiento total entre los extremos de la muestra es de 0.5 mm. Cuando la grieta ha crecido a 37 mm, el desplazamiento para esta misma carga es de 0.505 mm. El espécimen tiene 40 m de espesor. La carga de fractura de una muestra idéntica, pero con una longitud de grieta de 36 mm, es de 175 kN. Encuentra la dureza a la fractura\(K_{Ic}\) del material.