6.5: Fatiga

Introducción

El concepto de “fatiga” surgió varias veces en el Módulo sobre Fractura (Módulo 23), como en el crecimiento de grietas en los aviones Comet que derivaron al desastre cuando se hicieron lo suficientemente grandes como para propagarse catastróficamente como lo predice el criterio Griffith. La fatiga, como entienden los tecnólogos de materiales, es un proceso en el que se acumulan daños debido a la aplicación repetitiva de cargas que pueden estar muy por debajo del límite de elasticidad. El proceso es peligroso porque una sola aplicación de la carga no produciría ningún efecto malo, y un análisis de estrés convencional podría llevar a una suposición de seguridad que no existe.

En una visión popular de la fatiga en los metales, se cree que el proceso de fatiga comienza en un defecto interno o superficial donde se concentran las tensiones, y consiste inicialmente en un flujo de cizallamiento a lo largo de los planos de deslizamiento. A lo largo de varios ciclos, este deslizamiento genera intrusiones y extrusiones que comienzan a parecerse a una grieta. Una verdadera grieta que se extiende hacia adentro desde una región de intrusión puede propagarse inicialmente a lo largo de uno de los planos de deslizamiento originales, pero eventualmente se vuelve para propagarse transversalmente a la tensión normal principal como se ve en la Figura 1.

Figura 1: Modelo de intrusión-extrusión de inicio de grietas por fatiga.

Cuando se examina la superficie de falla de un espécimen fatigado, generalmente se evidencia una región de crecimiento lento de grietas en forma de “concha” concéntrica alrededor de la ubicación de la flf aw inicial. (Ver Figura 2.) La región de concha a menudo contiene “marcas de playa” concéntricas en las que la grieta fue detenida durante cierto número de ciclos antes de reanudar su crecimiento. Eventualmente, la grieta puede llegar a ser lo suficientemente grande como para satisfacer los criterios de energía o intensidad de tensión para una rápida propagación, siguiendo las expresiones anteriores para la mecánica de fractura. Esta fase final produce la superficie rugosa típica de fractura rápida. En el examen post mortem de piezas fallidas, a menudo es posible correlacionar las marcas de playa con casos específicos de sobreesfuerzo, y estimar la tensión aplicada al fallo a partir del tamaño de la grieta justo antes de la rápida propagación y la tenacidad a la fractura del material.

Figura 2: Superficies típicas de fatiga y falla. De B. Chalmers, Metalurgia Física, Wiley, p. 212, 1959.

El estudio moderno de la fatiga se remonta generalmente a la obra de A. Wohler, tecnólogo del sistema ferroviario alemán a mediados del siglo XIX. Wohler se mostró preocupado por la falla de los ejes después de varios tiempos en servicio, con cargas considerablemente menores de lo esperado. Un eje de vagón es esencialmente una viga redonda en flexión de cuatro puntos, lo que produce una tensión de compresión a lo largo de la superficie superior y una tensión de tracción a lo largo de la parte inferior (ver Figura 3). Después de que el eje haya girado media vuelta, la parte inferior se convierte en la parte superior y viceversa, por lo que las tensiones en una región particular de material en la superficie varían sinusoidalmente de tensión a compresión y viceversa. Esto ahora se conoce como carga de fatiga totalmente invertida.

Figura 3: Fatiga en un eje de vagón.

Curvas S-N

Mucho antes de que se desarrollara una comprensión microestructural de los procesos de fatiga, los ingenieros habían desarrollado medios empíricos para cuantificar el proceso de fatiga y diseñar contra él. Quizás el concepto más importante es el\(S-N\) diagrama, como los que se muestran en la Figura 4 (H.W. Hayden, W.G. Moffatt, y J. Wulff, The Structure and Properties of Materials, Vol. III, John Wiley & Sons, 1965.), en el que se aplica una amplitud\(S\) de tensión cíclica constante a un espécimen y se determina el número de ciclos de carga\(N\) hasta que falla el espécimen. Se podrían requerir millones de ciclos para causar fallas a niveles de carga más bajos, por lo que las abscisas generalmente se trazan logarítmicamente.

Figura 4:\(S - N\) curvas para aluminio y acero bajo en carbono.

En algunos materiales, en particular las aleaciones ferrosas, la\(S - N\) curva flf asiste eventualmente, de manera que por debajo de un cierto límite de resistencia no ocurre la\(\sigma_e\) falla por mucho tiempo que se ciclen las cargas. Obviamente, el diseñador dimensionará la estructura para mantener las tensiones\(\sigma_e\) por debajo de un factor de seguridad adecuado si se van a soportar cargas cíclicas. Para algunos otros materiales como el aluminio, no existe límite de resistencia y el diseñador debe hacer arreglos para que la vida útil planificada de la estructura sea menor que el punto de falla en la\(S - N\) curva.

La variabilidad estadística es problemática en las pruebas de fatiga; es necesario medir la vida útil de quizás veinte especímenes en cada uno de diez niveles de carga para definir la\(S - N\) curva con confianza estadística (A Guide for Fatigue Testing and the Statistical Analysis of Fatigue Data, ASTM STP-91-A, 1963 .). Generalmente es imposible ciclar la muestra a más de aproximadamente 10Hz (la inercia en los componentes de la máquina de prueba y el calentamiento de la muestra a menudo se vuelven problemáticos a velocidades más altas) y a esa velocidad se necesitan 11.6 días para alcanzar\(10^7\) los ciclos de carga. Obtener una\(S - N\) curva completa es obviamente un procedimiento tedioso y costoso.

Figura 5: Variabilidad en la vida útil a la fatiga y resistencia a la fractura.

A primera vista, la dispersión en los tiempos de vida medidos parece enorme, especialmente dada la escala logarítmica de las abscisas. Si el coeficiente de variabilidad en las pruebas de tracción convencionales suele ser de solo un pequeño porcentaje, ¿por qué las vidas de fatiga varían en órdenes de magnitud? Debe recordarse que en las pruebas de tracción, estamos midiendo la variabilidad en la tensión en un número dado de ciclos (uno), mientras que en la fatiga estamos midiendo la variabilidad en ciclos a una tensión dada. Dicho de otra manera, en las pruebas de tracción estamos generando barras de dispersión verticales, pero en fatiga son horizontales (ver Figura 5). Tenga en cuenta que debemos esperar más variabilidad en la vida útil a medida que la\(S - N\) curva se vuelve f atter, de modo que los materiales que son menos propensos al daño por fatiga requieren más especímenes para proporcionar un límite de confianza dado en la vida útil.

Efecto de la carga media

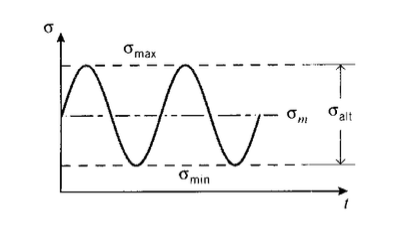
Por supuesto, no todas las aplicaciones de carga reales implican ciclos de estrés completamente invertidos. Un tipo de prueba de fatiga más general agrega una tensión media\(\sigma_m\) sobre la que se superpone un ciclo sinusoidal, como se muestra en la Figura 6. Tal ciclo puede formularse de varias maneras, una común es indicar la tensión alterna\(\sigma_{alt}\) y la relación de tensión\(R = \sigma_{\min}/\sigma_{\max}\). Para carga totalmente invertida,\(R = -1\). Un ciclo de tensión de\(R = 0.1\) se utiliza a menudo en las pruebas de componentes de aeronaves, y corresponde a un ciclo de tensión-tensión en el que\(\sigma_{\min} = 0.1 \sigma_{\max}\).

Figura 6: Media simultánea y carga cíclica.

Se requiere una cantidad muy sustancial de pruebas para obtener una\(S - N\) curva para el caso simple de carga completamente invertida, y generalmente no será práctico determinar familias enteras de curvas para cada combinación de tensión media y alterna. Hay una serie de estrategias para afinar esta dificultad, una común es el diagrama de Goodman que se muestra en la Figura 7. Aquí se construye una gráfica con tensión media como la abscisa y tensión alterna como la ordenada, y se dibuja una recta\ línea de vida” desde\(\sigma_e\) el\(\sigma_{alt}\) eje hasta la tensión de tracción final\(\sigma_f\) en el\(\sigma_m\) eje. Entonces, para cualquier tensión media dada, el límite de resistencia | el valor del estrés alterno en el que la fractura por fatiga nunca ocurre | se puede leer directamente como la ordenada de la línea de vida a ese valor de\(\sigma_m\). Alternativamente, si la aplicación de diseño dicta una relación dada de\(\sigma_e\) a\(\sigma_{alt}\), se dibuja una línea desde el origen con una pendiente igual a esa relación. Su intersección con la línea de vida le da entonces el límite de resistencia efectivo para esa combinación de\(\sigma_f\) y\(\sigma_m\).

Figura 7: El diagrama de Goodman.

Ley de minero por daños acumulados

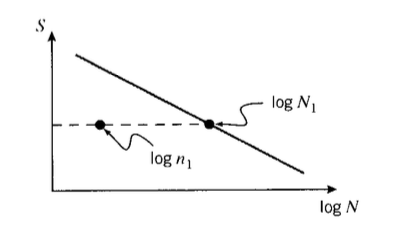
Cuando el nivel de carga cíclica varía durante el proceso de fatiga, a menudo se plantea la hipótesis de un modelo de daño acumulativo. Para ilustrar, tomar la vida para ser\(N_1\) ciclos a un nivel de estrés\(\sigma_1\) y\(N_2\) en\(\sigma_2\). Si se supone que el daño se acumula a un ritmo constante durante la fatiga y\(n_1\) se aplica una serie de ciclos a la tensión\(\sigma_1\), donde\(n_1 < N_1\) como se muestra en la Figura 8, entonces la fracción de vida útil consumida será\(n_1/N_1\). Para determinar cuántos ciclos adicionales sobrevivirá el espécimen a la tensión\(\sigma_2\), se dispondrá de una fracción adicional de vida de tal manera que la suma de las dos fracciones sea igual a una:

\(\dfrac{n_1}{N_1} + \dfrac{n_2}{N_2} = 1\)

Observe que aquí se utilizan ciclos absolutos y no ciclos logarítmicos. Resolviendo para los ciclos restantes permisibles en\(\sigma_2\):

 

La generalización de este enfoque se llama Ley de Minero, y se puede escribir

\[\sum \dfrac{n_j}{N_j} = 1\]

donde\(n_j\) es el número de ciclos aplicados a una carga correspondiente a una vida útil de\(N_j\).

Ejemplo\(\PageIndex{1}\)

Consideremos un material hipotético en el que la\(S - N\) curva sea lineal a partir de un valor igual al esfuerzo de fractura\(\sigma_f\) en un ciclo\((\log N = 0)\), cayendo a un valor de\(\sigma_f/2\) at\(\log N = 7\) como se muestra en la Figura 9. Este comportamiento puede ser descrito por la relación

 

El material ha sido sometido a ciclos de\(n_1 = 10^5\) carga a un nivel\(S = 0.6 \sigma_f\), y deseamos estimar cuántos ciclos puede soportar\(n_2\) el material ahora si elevamos la carga a\(S = 0.7 \sigma_f\). A partir de la\(S - N\) relación, sabemos que la vida en\(S = 0.6 \sigma_f =\) constante sería\(N_1 = 3.98 \times 10^5\) y la vida en\(S = 0.7 \sigma_f =\) constante sería\(N-2 = 1.58 \times 10^4\). Ahora aplicando la Ecuación 6.5.1:

Figura 9:\(S - N\) Curva lineal.

\(\dfrac{n_1}{N_1} + \dfrac{n_2}{N_2} = \dfrac{1 \times 10^5}{3.98 \times 10^5} + \dfrac{n_2}{1.58 \times 10^4} = 1\)

\(n_2 = 1.18 \times 10^4\)

La “ley” de Miner debe verse como muchas otras “leyes” materiales, una aproximación útil, bastante fácil de aplicar, que podría ser lo suficientemente precisa como para usarla en el diseño. Pero la acumulación de daños en la fatiga suele ser una mezcla complicada de varios mecanismos diferentes, y la suposición de acumulación de daño lineal inherente a la ley de Miner debe verse con escepticismo. Si porciones de la microestructura del material se vuelven incapaces de soportar la carga a medida que avanza la fatiga, la tensión debe ser llevada por los elementos microestructurales supervivientes. La tasa de acumulación de daño en estos elementos aumenta entonces, de manera que el material sufre daños mucho más rápidamente en las últimas porciones de su vida útil de fatiga. Si por otro lado las cargas cíclicas inducen mecanismos de fortalecimiento como la orientación molecular o el embotamiento de grietas, la tasa de acumulación de daño podría disminuir durante alguna parte de la vida útil del material. La ley del minero ignora tales efectos, y a menudo no logra capturar la física esencial del proceso de fatiga.

Tasas de crecimiento de grietas

Ciertamente en aviones, pero también en otras estructuras, es vital que los ingenieros sean capaces de predecir la tasa de crecimiento de grietas durante el ciclo de carga, para que la pieza en cuestión sea reemplazada o reparada antes de que la grieta alcance una longitud crítica. Una gran cantidad de evidencia experimental respalda la opinión de que la tasa de crecimiento de grietas puede correlacionarse con la variación cíclica en el factor de intensidad de estrés:

\[\dfrac{da}{dN} = A \Delta K^m\]

donde\(da/dN\) está la tasa de crecimiento de grietas por fatiga por ciclo,\(\Delta K = K_{\max} - K_{\min}\) es el rango de factores de intensidad de tensión durante el ciclo,\(A\) y\(m\) son parámetros que dependen del material, ambiente, frecuencia, temperatura y relación de estrés. Esto a veces se conoce como la “ley de París”, y conduce a tramas similares a la que se muestra en la Figura 10.

Figura 10: La ley de París para las tasas de crecimiento del crack por fatiga.

El exponente\(m\) suele estar cerca de 4 para los sistemas metálicos, lo que podría racionalizarse ya que la acumulación de daños está relacionada con el volumen\(V_p\) de la zona plástica: ya que el volumen\(V_p\) de la zona se escala con\(r_p^2\) y\(r_p \propto K_I^2\), entonces\(da/dn \propto \Delta K^4\). Algunos valores específicos de las constantes\(m\) y\(A\) para diversas aleaciones se dan en el Cuadro 1.

Cuadro 1: Parámetros numéricos en la ecuación de París.

aleación	\(m\)	\(A\)
Acero	3	\(10^{-11}\)
Aluminio	3	\(10^{-12}\)
Níquel	3.3	\(4 \times 10^{-12}\)
Titanio	5	\(10^{-11}\)

Ejercicio\(\PageIndex{1}\)

Un acero tiene una resistencia a la tracción máxima de 110 kpsi y un límite de resistencia a la fatiga de 50 kpsi. La carga es tal que la tensión alterna es 0.4 de la tensión media. Utilizando el método Goodman con un factor de seguridad de 1.5, encuentra la magnitud de la tensión alterna que le da un funcionamiento seguro.

Ejercicio\(\PageIndex{2}\)

Una aleación de titanio tiene una resistencia a la tracción máxima de 120 kpsi y un límite de resistencia a la fatiga de 60 kpsi. La tensión alterna es de 20 kpsi. Encuentre el estrés medio permisible, utilizando un factor de seguridad de 2.

Ejercicio\(\PageIndex{3}\)

Un material tiene una\(S - N\) curva que es lineal a partir de un valor igual al esfuerzo de fractura\(\sigma_f\) en un ciclo (\(\log N= 0\)), cayendo a un valor de\(\sigma_f/3\) at\(\log N = 7\). El material ha sido sometido a ciclos de\(n_1 = 1000\) carga a un nivel\(S = 0.7 \sigma_f\). Estime a cuántos ciclos puede soportar\(n_2\) el material si la amplitud de tensión se eleva ahora a\(S = 0.8 \sigma_f\).

Ejercicio\(\PageIndex{4}\)

Una aleación de acero tiene una\(S - N\) curva que cae linealmente de 240 kpsi en\(10^4\) ciclos a 135 kpsi en\(10^6\) ciclos. Una muestra se carga a 160 kpsi de tensión alterna para\(10^5\) ciclos, después de lo cual la tensión alterna se eleva a 180 kpsi. ¿Cuántos ciclos adicionales a esta tensión más alta se esperaría que sobreviva el espécimen?

Ejercicio\(\PageIndex{5}\)

Considera un cuerpo, lo suficientemente grande como para ser considerado infinito en dimensión lateral, que contiene una grieta central a través del espesor inicialmente de longitud\(2a_0\) y sometido a una tensión cíclica de amplitud\(\Delta \sigma\). Utilizando la Ley de París (Ecuación 6.5.2), muestran que el número de ciclos\(N_f\) necesarios para que la grieta crezca a una longitud\(2a_f\) viene dada por la relación

\(\ln (\dfrac{a_f}{a_0}) = A(\Delta \sigma)^2 \pi N_f\)

cuando\(m = 2\), y para otros valores de\(m\)

 

Ejercicio\(\PageIndex{6}\)

Utilizar la expresión obtenida en Ejercicio\(\PageIndex{5}\) para calcular el número de ciclos que un componente de acero puede sostener antes de la falla, donde la media longitud inicial de la grieta es de 0.1 mm y la media longitud crítica de la grieta para causar fractura es de 2.5 mm. La amplitud de tensión por ciclo es de 950 MPa. Toma la grieta para ser la de una grieta central en un plato infinito.

Ejercicio\(\PageIndex{7}\)

Utilizar la expresión desarrollada en Ejercicio\(PageIndex{1}\) para investigar si es mejor limitar el tamaño\(a_0\) de los defectos iniciales o extender el tamaño\(a_f\) del defecto en el que se produce la fractura rápida. La limitación\(a_0\) podría hacerse con una fabricación mejorada o mejores métodos de inspección, y el aumento\(a_f\) podría hacerse seleccionando un material con mayor tenacidad a la fractura. Para el caso “basal”, tomar\(m = 3.5, a_0 = 2\ mm\),\(a_f = mm\). Calcular el incremento porcentual en\(N_f\) dejando que (a) el tamaño inicial de f aw se reduzca a\(a_0 = 1\ mm\), y (b) aumentando el tamaño final de f aw a\(N_f = 10\ mm\).