9: Poniéndolo todo junto

Ciencia de la destilación (una mezcla de Química e Ingeniería Química)

Esta es la Parte IX, Poniendo Todo Junto de una serie de diez partes de artículos técnicos sobre la Ciencia de la Destilación, como se practica actualmente a nivel industrial. Véase también la Parte I, Panorama general para los comentarios introductorios, los alcances de la serie de artículos y la nomenclatura.

La Parte IX, Poniéndolo Todo Junto utiliza la información de las Partes III a VII, mostrando cómo combinarlas en un ejemplo práctico para la separación masiva; y cómo el uso de las técnicas detalladas en artículos anteriores da respuestas que difieren de los ideales de la Ley básica de Raoult/Dalton aplicación.

Ver artículos anteriores por el siguiente detalle:

• Parte III para propiedades críticas y factor acéntrico, especialmente Tabla 3-3
• Parte IV para la ecuación de presión de vapor recomendada, especialmente la Ecuación 4-3 y la Tabla 4-1
• Parte V para la Ecuación de Estado, especialmente las Ecuaciones 5-3 y 5-4
• Parte VI, especialmente la Ecuación 6-4 para la presión parcial y las Ecuaciones 6-7 y 6-8 para los coeficientes de fugacidad
• Parte VII para Coeficientes de Actividad Líquida, especialmente Ecuación 7-3

En este artículo se desarrolla un ejemplo práctico de destilación, mostrando la relación Y/X con la temperatura para el sistema binario DCS-TCS con presión constante a 11.0 atmósferas, y mostrando los resultados como una gráfica T XY /P así como en forma tabular. A partir de tales datos, un diseñador de columnas de destilación consideraría la mejor disposición para la alimentación de la columna, recuperación de “partes superiores” y “fondos”, recuento de bandejas y relación de reflujo externo (y a partir de eso, la energía requerida para el calderín y condensador, así como la carga hidráulica por unidad de flujo másico de materia prima). Se elaboran dos variaciones de este ejemplo, que muestran la aplicación de la ciencia de la destilación: una que solo usa Raoult/Dalton ideal, y otra que utiliza el conjunto completo de coeficientes de partida de idealidad. La salida de la tabla y las gráficas a continuación se realizan utilizando MS Excel. Luego al final del artículo, los resultados de la tabla se demuestran gráficamente usando una gráfica McCabe-Theile para separar las charolas para una tasa de reflujo apropiada y mostrar la mejor bandeja de alimentación.

La tabla de la Figura 9-1 se configura para cubrir el rango de fracción molar líquida de DCS de unidad a cero, en incrementos de 0.05 fracción molar, con 0.01/0.99 fracción molar añadida para ilustrar los efectos asintóticos. Para cada fila de tabla distinta de cero, primero se asume una temperatura, y luego se calculan las fracciones molares de vapor por Raoult/Dalton, con p=11.0 atmósferas; luego la temperatura de esa fila se ajusta iterativamente hasta que la presión total = 11.0 atmósferas.

En la gráfica de la Figura 9-1 se muestran los resultados del cálculo en forma T XY /P, con el valor de X _DCS =1.0 representando el producto “tops” más apretado posible en el condensador de la columna de destilación; y un valor de X _DCS =0.0 representando el más apretado posible producto de “fondos” en el rehervidor de columna, todo en una condición de reflujo total. Para una columna finita, la fracción molar del producto “tops” sería un cultivo de los valores superiores X _DCS de las curvas T XY /P; y la fracción molar del producto de “colas” a sería un cultivo de los valores menores de X _DCS del T XY /P curvas. En tal caso, la bandeja de alimentación de la columna se identificaría como ese punto en la columna donde la temperatura de la bandeja es idéntica al punto de ebullición de la mezcla de alimentación. La gráfica adjunta de solución muestra cómo serían las curvas T XY /P, para tal solución de Raoult/Dalton al binario DCS-TCS a 11.0 atmósferas.

\( Y_{1}=(X_{1} \times VP_{1})/(X_{1} \times VP_{1} + X_{2} \times VP_{2}) \nonumber\)\( Y_{2}=(X_{2} \times VP_{2})/(X_{1} \times VP_{1} + X_{2} \times VP_{2}) \nonumber\)repetir Ecuación 6-1

Figura 9-1, Tabla de cálculo y gráfica TXY, Raoult/Dalton

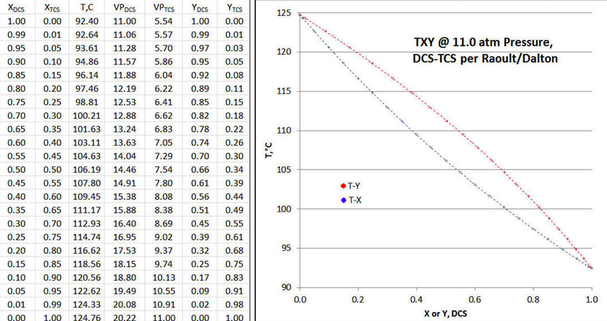
Si se examina cuidadosamente la gráfica de datos de la gráfica de la Figura 9-1, se puede ver que las curvas T-X y T-Y son exactamente simétricas cuando se “pliegan” a lo largo de una línea que va desde puntos de abscisa/ordenada de (0,124.76) a (1,92.40); o “plegadas” ortogonalmente a esa misma línea. Es decir, no hay desviaciones de la idealidad ni en fase vapor ni líquida, ya sea con DCS o TCS.

Ahora X e Y se vuelven a calcular incluyendo las desviaciones de la idealidad, tanto en fugacidad (ø) como en Coeficientes de Actividad Líquida (\(\gamma \nonumber\)).

Figura 9-2, tabla de cálculo TXY/P, todos los factores de salida incluidos

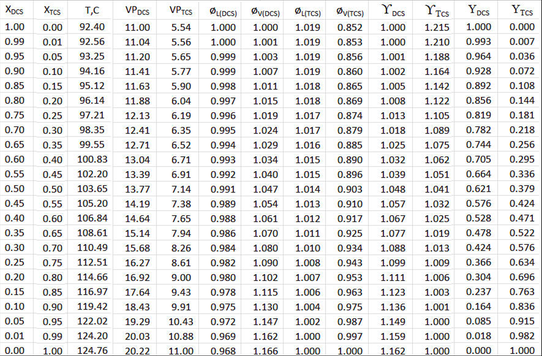
También se configura la tabla de la Figura 9-2 anterior y se realizan cálculos por filas para cada valor de X _DCS, pero los coeficientes de fugacidad en fase líquida y vapor (ø _L y ø _V) y los coeficientes de actividad (\(\gamma_{i} \nonumber\)) se incluyen en el cálculo del vapor fracciones molares (\(\gamma_{DCS} \nonumber\)). Para cada fila, la temperatura se itera hasta la suma de presiones parciales = 11.0 atmósferas. Tenga en cuenta que dado que los coeficientes de actividad son funciones suaves de temperatura, cada fila tiene sus propias constantes de Van Laar determinadas y el valor\(\gamma \nonumber\) calculado para la fracción molar líquida de esa fila. Así, se incluyen todos los factores de salida de la idealidad.

\[ Y_{i}= (\phi_{i}^L \times \gamma_{i} \times VP_{i} \times X_{i})/(\phi_{i}^V \times \pi) \label{9-1} \]

que es un reordenamiento algebraico de la Ecuación 6-4 de la Parte VI anterior.

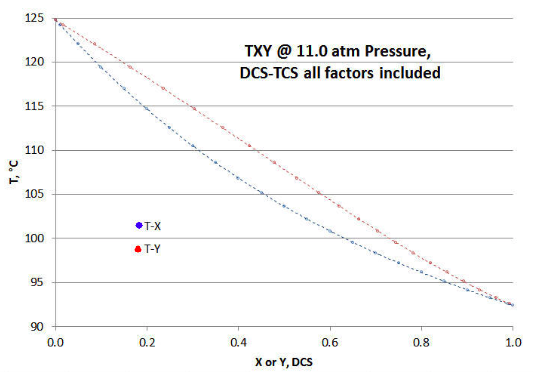
Para mostrar mejor cómo los diversos factores de desviación de idealidad impactan en la gráfica T XY /P (en comparación con la Figura 9‑1 anterior), se grafica la tabla de la Figura 9-2. La simetría de la gráfica Figura 9-1 Raoult/Dalton ya no está ahí, ni a lo largo de la línea de “pliegue” que va desde los puntos de abscisa/ordenada de (0,124.76) a (1, 92.40); o “plegada” ortogonalmente a esa misma línea. Obsérvese también que las curvas T-X y T-Y están más próximas entre sí en la Figura 9‑3, a diferencia de la Figura 9-1.

Figura 9-3, parcela TXY/P, todos los factores de salida incluidos

Para una aproximación muy simple del recuento de bandejas, para un producto dado de columna de destilación “tops”, fracciones molares de producto de “colas” y mezcla de alimentación, y para una tasa de reflujo dada, se construye una gráfica McCabe-thiele en la Figura 9-4 para separar gráficamente el número de bandejas por encima y por debajo de la bandeja de alimentación. Para casi todas las aplicaciones industriales, este análisis bandeja por bandeja se realiza mediante modelado por computadora, como ASPEN, VMG, HYSYS, ChemCAD, etc. Para aplicar la técnica a un modelo de computadora, el usuario especificaría las constantes críticas (según la Parte III), la ecuación de presión de vapor a usar (según Parte IV), la EOS que se utilizará para calcular los coeficientes de fugacidad (según la Parte V) y el modelo de Coeficiente de Actividad Líquida que se utilizará (según la Parte VI).

Para construir una gráfica de McCabe-Thiele, el equilibrio X - Y (en rojo abajo) se representa en un conjunto de ejes donde X = fracción molar líquida del componente más volátil = X _DCS; e Y = fracción molar de vapor del componente más volátil = Y _DCS. La línea de reflujo total (en negro abajo) conecta (X, Y) = (0,0) y (1,1); representando el reflujo máximo posible. Las líneas se agregan (en azul discontinuo abajo) para la alimentación (X _F), y el producto destilado (X _D) y el producto de fondo (X _B), desde el eje X hasta la línea de reflujo total. La línea de alimentación se extiende hacia la curva de equilibrio, y desde esa intersección se dibuja una línea hasta el final de la línea de producto destilado. La pendiente de esa línea dibujada representa el reflujo interno mínimo necesario para hacer la separación (es decir, con un número infinito de charolas). Luego se dibuja la línea de operación de la columna superior (en magenta abajo) conectando el extremo de la línea de producto destilado con la línea de alimentación, con una pendiente algo mayor que la pendiente mínima de reflujo. En la práctica normal la pendiente de la línea operativa de la columna superior suele ser de aproximadamente 1.3 veces la pendiente mínima, dependiendo del valor relativo de la energía operativa vs costo de capital. Luego se dibuja la línea de operación de la columna inferior, intersecando la línea de producto de fondo con la línea de operación de la columna superior (y la línea de alimentación). El número de bandejas teóricas (también conocido como etapas) puede entonces ser escalonado (en verde abajo) de X _D a X _B, y determinar la mejor bandeja para la alimentación.

Figura 9-4, solución de McCabe Thiele para cálculos de ejemplo

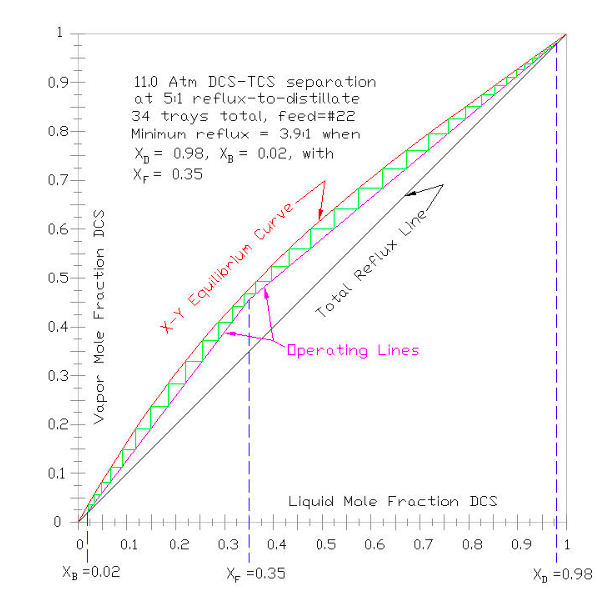
Para ilustrar un ejemplo de uso de una gráfica de McCabe-Thiele, supongamos que la mezcla a separar es un líquido molar DCS 35%, precalentado a su punto de ebullición de 108.61°C (como se muestra en el 35% de la Figura 9-2). “Además, supongamos que el producto destilado “" tops "” de la columna debe ser 98% molar de DCS y el producto de “" fondos "” de la columna debe ser 98% molar de TCS.” Según el texto anterior, se determina que el reflujo mínimo (es decir, la pendiente de la línea entre X _D = X _DCS de 0.98, X _B = X _DCS de 0.02) es de 3. 9:1, reflujo a destilado. Para permitir un número razonable de charolas, se elige una tasa de reflujo de 5:1 (aproximadamente 1.3 veces el mínimo), por lo que la pendiente de la línea de operación de la columna superior es R/ (R+1) = 5/ (5+1) =0.8333. Al salir de las bandejas, se determina que el número total de charolas teóricas requeridas es 34, con la bandeja de alimentación en #22. El conteo convencional de bandejas comienza en el condensador de columna = bandeja #1.

Como se puede observar al examinar la Figura 9-4, a medida que aumenta la tasa de reflujo de la columna, la pendiente de la línea operativa de la columna superior (magenta) aumenta y se abre la brecha entre la Línea de Equilibrio X-Y (roja) y la Línea de Reflujo Total (negra). Por lo que al aumentar el reflujo se disminuye el número de charolas requeridas para realizar la separación especificada.

En una aplicación normal de procesos industriales, todos los cálculos se realizan a través de simuladores por computadora, lo que permite variaciones en la pendiente de la línea de operación; condición de calidad de alimentación (por ejemplo, vapor saturado, líquido saturado, líquido subenfriado, etc.); cambios en las relaciones de flujo líquido/vapor internos debido a la física propiedades; efectos de calor ambiente; eficiencias de bandeja, etc.; así como integrar la columna de destilación en el resto del diseño del proceso. Entonces el método McCabe-Thiele solo se usa para la explicación gráfica.

Sin embargo, la consideración principal del diseño de la columna de destilación es la relación de equilibrio X-Y. Si esto tiene un error considerable, como usar solo Raoult/Dalton, el diseño de la columna será un fracaso. Dado que el costo de los sistemas de destilación a escala industrial es de millones de dólares (decenas de $MM para los más grandes), hay muchas razones para que la relación de equilibrio X-Y sea correcta.

En el ejemplo de este artículo, el modelo básico de Raoult/Dalton daría como resultado que la relación de equilibrio X-Y en el ejemplo anterior tuviera más curvatura (que la mostrada en la Figura 9-4) y por lo tanto más espacio abierto entre la curva de equilibrio y las líneas de operación. El reflujo resultante determinado sería aproximadamente 2/3 del requerido, y el número de charolas requeridas también sería aproximadamente 2/3 de las necesidades, por lo que un error importante en el diseño. Dado lo que está en juego financieramente, no cabe duda de que el uso de una ciencia de destilación adecuada bien merece la pena, aunque los conceptos sean complejos y los cálculos sean tediosos.