8: Métodos de análisis VLE
- Page ID
- 82489
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ciencia de la destilación (una mezcla de Química e Ingeniería Química)
Se trata de la Parte VIII, Métodos de Análisis VLE de una serie de diez partes de artículos técnicos sobre la Ciencia de la Destilación, como se practica actualmente a nivel industrial. Véase también la Parte I, Panorama general para los comentarios introductorios, los alcances de la serie de artículos y la nomenclatura.
Parte VIII, Métodos de Análisis VLE recomienda la metodología utilizada al recolectar datos de los Coeficientes de Actividad Líquida de los sistemas binarios (ver Parte VII). Este artículo también trata de la validación, especialmente cuando la recolección de datos se realiza en fluidos reactivos como los clorosilanos que pueden desproporcionarse o dimerizar durante el estudio.
Este artículo utiliza la información de las Partes III a VII.
En la Parte VII se dio una técnica de correlación para estimar los Coeficientes de Actividad Líquida. Como se mencionó en el artículo anterior, es común recolectar dichos datos de equilibrios vapor-líquido (VLE) en el laboratorio, en condiciones cercanas a la presión ambiente. Sin embargo, muchas aplicaciones industriales frecuentemente necesitan usar resultados de VLE a presiones de proceso/temperaturas más altas o diferentes composiciones. Para evitar la confusión de notación entre el coeficiente de actividad líquida (\(\gamma_{i} \nonumber\)) y la fracción molar de vapor (Y i), las fracciones molares X e Y se muestran en negritas.
Recordemos de las Partes VI y VII que los coeficientes de fugacidad (\(\phi_{i}^V\nonumber\)&\(\phi_{i}^L\nonumber\)) son funciones de temperatura y presión. Sin embargo, los Coeficientes de Actividad Líquida (s\(\gamma_{i} \nonumber\)) son funciones de solo temperatura y fracción molar. En una situación experimental, los valores calculados de\(\gamma_{i} \nonumber\) (a partir de los valores de Y i y X i = fracción molar en fase vapor y fracción molar en fase líquida) son más fáciles de correlacionar cuando la temperatura del sistema se mantiene constante, y se permite que la presión del sistema variar. Dicho de otra manera, P XY data @ constante T es mucho más fácil de recolectar y correlacionar que T XY @ constante P. Sin embargo, en aplicaciones comerciales la columna de destilación se controla típicamente a presión constante. Entonces, un error común de comunicación industrial es solicitar al laboratorio que recoja datos de VLE como T XY @P, pero en su lugar obtener P XY @T en su lugar. Hay una manera de convertir un conjunto de datos a la otra relación, pero es algo incómoda y requiere elegir el modelo de coeficiente de actividad.
En la Figura 7-1 de la Parte VII, se muestra el perfil esperado de\(\gamma \nonumber\) vs X @ constante T, y en la Figura 7-2 de la Parte VII se muestra el perfil esperado de\(\gamma \nonumber\) vs T @ constante X, en los ejes X =0 y X =1. La razón para generar coeficientes de actividad líquida experimentalmente es normalmente utilizar los resultados de laboratorio para el diseño de la columna de destilación, con la confianza que se\(\gamma \nonumber\) puede conocer con precisión a cualquier valor de X o T, para establecer la relación Y/X arriba y abajo del diseño de la columna. Utilizando los principios de las Partes VI y VII, estos problemas pueden resolverse.
Una vez establecido el protocolo experimental, es necesario considerar el impacto de los equipos de recolección de datos en los fluidos analizados y validar la calidad de los fluidos de muestra. Para fluidos reactivos como los clorosilanos, eso significa que el uso de cristalería con capacidad de presión es la mejor opción (o acero revestido de níquel como segunda opción), ya que algunos de los elementos de aleación del acero inoxidable catalizarán lentamente las reacciones de desproporción, que alteran las composiciones de la muestra.
Además, es importante validar la pureza de las muestras de fluido, en lugar de aceptar ciegamente el análisis de cualquier información de proveedor acompañante. Nuevamente, con los clorosilanos (como típicos de los fluidos reactivos), el contenedor de envío puede catalizar reacciones secundarias (es decir, el COA del proveedor quizás fue exacto cuando la muestra se cargó en el contenedor, pero la pureza se degradó durante el envío). Es común que las muestras de TCS puras al 99.99% (bajo inertización de argón) de proveedores acreditados terminen teniendo varios por ciento de DCS y varios por ciento de STC, junto con algunas décimas por ciento de hexaclorodisilano y algunas décimas por ciento de gas hidrógeno, cuando se usan apenas unas semanas después. Una buena práctica antes de cargar fluidos de muestra en el equipo de laboratorio es destilar dos veces las muestras (descartando las fracciones “ligeras” y “pesadas”, y asegurando que solo se usa la fracción “cortada del corazón”: cuya presión de ebullición es idéntica a la presión de vapor del componente puro esperada).
Con las precauciones anteriores, los datos se recolectan en 15-20 (o más) puntos X, Y, con algunos duplicados más adelante en la ejecución para establecer la precisión del análisis experimental y confirmar la ausencia de error sistémico (como contaminación). Al menos dos pares de puntos de datos deben recopilarse cerca de X= cero y X= unidad. Para ayudar a confirmar la dependencia de temperatura de los coeficientes de actividad, se deben recolectar al menos tres conjuntos de datos (cada uno a una temperatura o presión constante diferente).
Después de la recolección de datos, el trabajo de laboratorio se suspende, pero luego se necesita “procesamiento de números” para confirmar la validez de los datos antes de informar o usar los resultados. Si no se confirma la validez de los datos, se debe encontrar el error y repetir el trabajo de laboratorio. Primero, trazar el conjunto de datos y verificar que tanto la curva P-X como la curva P-Y, o la curva T-X y la curva T-Y muestran una intersección idéntica, tanto en los ejes de fracción molar cero como unitaria; y que las intersecciones de ejes son exactamente representativas de cada puro- presión de vapor conocida del componente. Si las curvas X e Y no se cruzan en el valor correcto en cada eje, hay algún error sistemático en el conjunto de datos que debe resolverse antes de realizar más trabajos de evaluación. Es probable que un conjunto de datos corrupto tenga un valor mínimo para establecer coeficientes de actividad; y más a menudo es una razón para desecharlo todo y volver a hacer el trabajo, después de que se resuelva el error sistémico.
Usando una modificación algebraica de la Ecuación 6-4 anterior, los coeficientes de actividad, se calculan los\(\gamma_{i} \nonumber\) i para cada punto de datos P- X y P- Y.
\[\gamma_{i} =(\phi_{i}^V/\phi_{i}^L) \times (Y_{i} \times \pi)/(VP_{i} \times X_{i}) \label{8-1} \]
donde\(\pi \nonumber\) es la presión total,\(VP_{i} \nonumber\) es la presión de vapor del i-ésimo componente, y\((\phi_{i}^V/\phi_{i}^L) \nonumber\) es la relación de fugacidad vapor/líquido de ese componente.
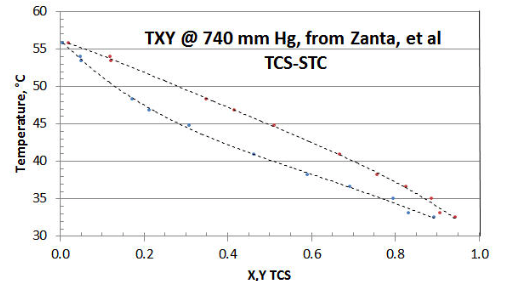
En la Figura 8-1 se muestra el conjunto de datos T XY /P de doce puntos de Zanta et al, de Chemicky Prumysl (Czech Chemical Industry), utilizando una gráfica de hoja de cálculo. Los investigadores sí recopilaron algunos puntos de datos cerca del eje STC (es decir, TCS= cero). Sin embargo, habría sido preferible tener algunos más recopilados cerca del otro eje (es decir, TCS= unidad); y que todos los datos se reportaran con mayor precisión. Los investigadores optaron por recolectar datos a una presión constante de 740 mm Hg (a diferencia del método P XY /T más preferible que evite la necesidad de ajustar el Coeficiente de Actividad Líquido calculado\(\gamma \nonumber\) para cambiar la temperatura), por razones de su equipo de laboratorio y simplificar su procedimiento; y para recopilar únicamente un conjunto de datos T XY /P.
Si solo se consideran los datos brutos, parecería que las curvas T-X y T-Y podrían no intersecarse mutuamente en el eje STC, o que la intersección es mayor que la temperatura esperada de 56.2°C representativa de la vaporización STC @ 740 mm Hg. La razón es que la precisión individual del punto de datos es baja en la región del eje STC.
Sin embargo, con el alisado de datos y la extrapolación de las curvas T-X y T-Y a través de algún ajuste de curvas de hoja de cálculo, las dos curvas parecen muy probablemente intersectar el eje STC cerca de la temperatura esperada de 56.2°C. Sin embargo, en el eje TCS, el ajuste de curva de los datos T-X y T-Y parece que ambos dan como resultado su intersección en el eje TCS a 30.0°C, a diferencia de los 32.3°C esperados para TCS puro. La explicación más probable para esta discrepancia de conjunto de datos es que la muestra de TCS suministrada fue una mezcla desproporcionada de DCS/TCS/STC tal como se recibió, y/o los fluidos en el equipo desproporcionaron como resultado de los materiales de construcción del equipo. Una temperatura del eje TCS de 30.0°C es representativa de una mezcla líquida de 5% DCS/ 95% TCS. Sorprendentemente, el procedimiento analítico de los investigadores no recogió el pico de DCS, lo que habría revelado la corrupción de la muestra (pero ese es un error común al usar ese tipo de analizador del investigador).
Ahora que el conjunto de datos ha sido desacreditado, queda por ver qué -si la hay- se puede extraer información útil. Aparte de demostrar técnica, hay poco uso en la reducción de los datos que son altos en “mal TCS” para conseguir que la\(\gamma \nonumber\) asíntota se interseque con el eje TCS. Esto se debe a que las fracciones molares X TCS* están cambiando a lo largo de la curva del coeficiente de actividad STC (aproximadamente una relación 1:19 de DCS/TCS, cayendo en relación a muy poco DCS en la mezcla ternaria, cerca de 56.2°C en el eje STC). Sería imposible adivinar qué valores de propiedad son los mejores para usar para los coeficientes de fugacidad, dado un contenido DCS “comodín”). Los datos más cercanos a intersectar el eje STC podrían ser interpolados para formar unos “pseudo-puntos” cercanos a X TCS =0, con el fin de obtener un valor aproximado de la\(\gamma \nonumber\) asíntota TCS (basado en el supuesto de que hay poco DCS en la mezcla ternaria en ese punto). Sin embargo, incluso pequeñas cantidades de DCS cerca del área X TCS =0 podría esperarse que ejerzan un efecto significativo de Coeficiente de Actividad Líquida, y los valores de fugacidad podrían estar algo en error al asumir solo los valores de propiedad de TCS.
Sin embargo, para ilustrar la técnica de reducción de datos para los datos T XY /P (a diferencia de la forma P XY /T preferida), se evalúan algunos “pseudo-puntos” cerca del eje.
Usando un ajuste de curva de cuarto orden, con la temperatura del eje STC establecida en 56.20°C, las ecuaciones de ajuste de curva T-X y T-Y son, respectivamente, a través de funciones de ajuste de curvas de hoja de cálculo:
T- X\(T=18.949x^4-64.825x^3+75.709x^2-56.044x+ 56.20 \nonumber\)
T-Y\(T=-22.243y^4+33.158y^3-18.028y^2-19.075y+ 56.20 \nonumber\)
A partir de esos dos ajustes de curva, se calculan los siguientes “pseudo-puntos”, resolviendo las ecuaciones cuarticas para T-X y T-Y:
|
P, mm Hg |
T, °C |
X TCS* |
\(\gamma \nonumber\)TCS* |
|---|---|---|---|
|
740 |
56.2 |
0.0000 |
\ (\ gamma\ nonumber\) TCS*” valign="top” width="174" class="lt-eng-8146">
0.0000 |
|
740 |
55.0 |
0.00359 |
\ (\ gamma\ nonumber\) TCS*” valign="top” width="174" class="lt-eng-8146">
0.0104 |
|
740 |
54.0 |
0.0415 |
\ (\ gamma\ nonumber\) TCS*” valign="top” width="174" class="lt-eng-8146">
0.1065 |
|
740 |
53.0 |
0.0620 |
\ (\ gamma\ nonumber\) TCS*” valign="top” width="174" class="lt-eng-8146">
0.1515 |
En la Tabla 8-1, X TCS* e Y TCS* están subinscritos como “TCS*” para denotar que mientras las propiedades de TCS se utilizan para la estimación de la presión de vapor y fugacidad, el fluido más volátil es realmente una mezcla DCS/TCS. El punto de datos en X, Y = 0.0000, 0.0000 se da solo para mostrar la intersección del eje STC, pero no se puede usar para calcular la\(\gamma \nonumber\) asíntota ya que eso resultaría en “división por cero” en la Ecuación 7-1.
Usando las propiedades de TCS, los valores para VP, ø L y ø v se calculan según las Partes IV, V y VI, y los resultados se muestran en la Tabla 8-2 para\(\gamma \nonumber\) TCS* calculado a 740 mm Hg (para cada temperatura de “pseudo-punto”).
|
P, mm Hg |
T, °C |
VP TCS* |
ø L |
ø v |
\(\gamma \nonumber\)TCS* |
|---|---|---|---|---|---|
|
740 |
56.2 |
2.130 |
0.9983 |
1.0321 |
\ (\ gamma\ nonumber\) TCS*” valign="top” width="126">
por determinar |
|
740 |
55.0 |
2.055 |
0.9984 |
1.0316 |
\ (\ gamma\ nonumber\) TCS*” valign="top” width="126">
1.418 |
|
740 |
54.0 |
1.994 |
0.9984 |
1.0311 |
\ (\ gamma\ nonumber\) TCS*” valign="top” width="126">
1.294 |
|
740 |
53.0 |
1.934 |
0.9984 |
1.0307 |
\ (\ gamma\ nonumber\) TCS*” valign="top” width="126">
1.270 |
Los valores calculados para\(\gamma \nonumber\) TCS* en la Tabla 8-2 se basan en los “pseudo-puntos” X, Y del Cuadro 8-1 y utilizando la ecuación E (\ ref {8-1}) anterior, para demostrar la metodología de reducción de datos experimentales. La tendencia sobre los coeficientes de fugacidad y el coeficiente de actividad es correcta: los valores ø L aumentan hacia la unidad a medida que X TCS* aumenta hacia la unidad; los valores ø v disminuyen hacia la unidad a medida que X TCS* aumenta hacia la unidad\(\gamma \nonumber\) Los valores de TCS* disminuyen hacia la unidad cuando X TCS* aumenta hacia la unidad.
La asíntota en el eje STC se determina extrapolando el valor de\(\gamma \nonumber\) TCS* de los tres “pseudo-puntos”. (Esa curva tendría una pendiente diferente con respecto a la composición si se tratara de datos T XY /P, ya que la temperatura está cambiando así como X TCS* en la Tabla 7-2.) Esta técnica identifica la\(\gamma \nonumber\) asíntota TCS* como 1.437 (el valor promedio de\(\gamma \nonumber\) TCS* obtenido extrapolando ajustes de curva de\(\gamma \nonumber\) TCS* vs X TCS* a un valor cero de X TCS*, y \(\gamma \nonumber\)TCS* vs Y TCS* a un valor cero de X TCS*). En comparación con los datos de otros investigadores, la asíntota calculada tiene un alto valor. También parece alto por expectativa de la Ecuación 7-3 de la Parte VII, lo que indicaría un valor más cercano a 1.21 @ 56.2°C, o 1.23 @ 32.3°C (el punto de ebullición TCS esperado a 740 mm Hg). Posiblemente existe un error por el contenido de DCS, lo que tendería a hacer altos los valores de\(\gamma \nonumber\) TCS* calculados al aumentar la fracción molar no STC en el vapor. La técnica de ajuste de curvas podría estar “desactivada” ya que hubo baja precisión en los dos pares de datos cercanos al eje X TCS* =0.
Esto demuestra que simplemente no hay una buena manera de “arreglar” datos que tienen errores sistemáticos en ellos: prácticamente todos los textos sugieren que cuando se encuentran datos corruptos, no tiene sentido continuar con el análisis de datos. Además de determinar valores asintóticos razonables en ambos ejes, Reid, Prausnitz y Sherwood sugieren en “Las propiedades de los gases y líquidos”, que todos los valores\(\gamma \nonumber\) calculados se ajusten primero a una base de temperatura común (usando la aproximación de\(Ln(\gamma) \times = constant \nonumber\)), luego usar el Gibbs- Ley Duhem para establecer la consistencia termodinámica. Si bien técnicamente es la mejor manera de validar los datos para su consistencia, requiere una cantidad significativa de datos de alta calidad, y se sugiere solo si se deben considerar modelos avanzados de Coeficiente de Actividad Líquida (por ejemplo, NRTL o UNIQUAC). Para Van Laar, Margules, Wilson o modelos similares de dos constantes, deben ser suficientes 15-20 puntos de datos.
Siempre es mejor tener menos puntos de datos, pero tener el conjunto de datos internamente consistente, en lugar de una gran cantidad de puntos de datos posiblemente corruptos.
Este artículo sugiere utilizar el modelo Van Laar para coeficientes de actividad basados en resultados razonables con análisis de datos sobre clorosilanos, y el éxito en la predicción de las constantes de Van Laar a través de la Ecuación 7-3 en la Parte VII. Sin embargo, el lector puede querer explorar otros modelos para un mejor ajuste a los datos experimentales, después de que dichos datos hayan sido validados. En “Las propiedades de los gases y los líquidos”, los autores dan una lista exhaustiva de otros modelos de coeficientes de actividad a considerar, con algunas notas sobre “pro & con”.


