1.6: Ley de Gauss
- Page ID
- 86337
Ahora tenemos que revisar alguna teoría de campo. Estaremos usando campos de vez en cuando en este curso, y cuando necesitemos algún aspecto de la teoría de campos, introduciremos lo que necesitamos en ese momento. Esto parece tener más sentido que pasar varias semanas hablando de mucha teoría abstracta sin ver cómo o por qué puede ser útil.
Lo primero que debemos recordar es la Ley de Gauss. La Ley de Gauss, como la mayoría de las leyes fundamentales del electromagnetismo, no proviene del primer principio, sino de la observación empírica y de los intentos de hacer coincidir los experimentos con algún tipo de marco matemático autoconsistente. La Ley de Gauss establece que:\[\begin{array}{l} \oint\limits_{s,} D \ dS &= \ Q_{\text{encl}} \\ &= \ \oint \limits_{v,} \rho (v) \ dV \end{array} \nonumber \]
donde\(D\) está el vector de desplazamiento eléctrico, que está relacionado con el vector de campo eléctrico,\(E\), por la relación\(D = \varepsilon E\). \(\varepsilon\)se llama la constante dieléctrica. En silicio tiene un valor de\(1.1 \times 10^{-12} \ \frac{\mathrm{F}}{\mathrm{cm}}\). (Tenga en cuenta que\(D\) debe tener unidades de\(\frac{\mathrm{Coulombs}}{\mathrm{cm}^{2}}\) para que todo funcione bien.) \(Q_{\mathrm{encl}}\)es la cantidad total de carga encerrada en el volumen\(V\), la cual se obtiene haciendo una integral volumétrica de la densidad de carga\(\rho (v)\).
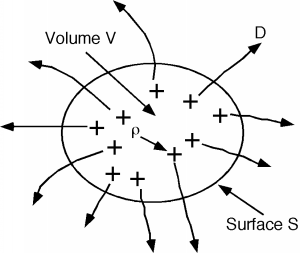
La ecuación\(\PageIndex{1}\) solo dice que si se suma la integral de superficie del vector de desplazamiento\(D\) sobre una superficie cerrada\(S\), lo que se obtiene es la suma de la carga total encerrada por esa superficie. Por útil que sea, la forma integral de la Ley de Gauss, (que es lo que\(\PageIndex{1}\) es la Ecuación) no nos ayudará mucho a entender los detalles de la región de agotamiento. Tendremos que convertir esta ecuación a su forma diferencial. Esto lo hacemos primero reduciendo el volumen\(V\) hasta que podamos tratar la densidad de carga\(\rho (v)\) como una constante\(\rho\), y reemplazar el volumen integral con un producto simple. Ya que estamos haciendo\(V\) pequeños, llamémoslo\(\Delta (V)\) para recordarnos que estamos hablando de apenas una pequeña cantidad. \[\oint\limits_{\Delta (v),} \rho (v) \ dV \rightarrow \rho \Delta (v) \nonumber \]
Y así, la Ley de Gauss se convierte en:\[\begin{array}{l} \oint\limits_{s,} D \ dS &= \varepsilon \oint\limits_{s,} E \ dS \\ &= \rho \Delta (V) \end{array} \nonumber \] o\[\frac{1}{\Delta V} \left(\oint\limits_{s,} E \ dS\right) = \frac{\rho}{\varepsilon} \nonumber \]
Ahora bien, por definición el límite del lado izquierdo de la Ecuación\(\PageIndex{4}\) como\(\Delta (V) \rightarrow 0\) se conoce como la divergencia del vector\(\mathbf{E}\), o\(\mathrm{div} \mathbf{E}\). Así tenemos\[\lim_{\Delta (V) \rightarrow 0} \frac{1}{\Delta (V)} \left(\oint\limits_{s,} E \ dS\right) = \mathrm{div} (\mathbf{E}) = \frac{\rho}{\varepsilon} \nonumber \] Nota lo que esto dice sobre la divergencia. La divergencia del vector\(\mathbf{E}\) es el límite de la integral superficial de\(\mathbf{E}\) sobre un volumen\(V\), normalizado por el propio volumen, ya que el volumen se contrae a cero. Me gusta pensar que es una especie de “integral de superficie puntual” del vector\(\mathbf{E}\).

Si\(\mathbf{E}\) sólo varía en una dimensión, que es con lo que estamos trabajando ahora mismo, la expresión de la divergencia es particularmente sencilla. Es fácil resolver qué es a partir de una simple imagen. Mirando Figura\(\PageIndex{2}\) vemos que si solo\(\mathbf{E}\) se apunta a lo largo de una dirección (digamos\(x\)) y es solo una función de\(x\), entonces la integral de superficie de\(\mathbf{E}\) sobre el volumen\(\Delta (V) = \Delta (x) \Delta (y) \Delta (x)\) es particularmente fácil de calcular. \[\oint\limits_{s,} E \ dS = \mathbf{E} (x+\Delta (x)) \Delta (y) \Delta (z) - \mathbf{E}(x) \Delta (y) \Delta (z) \nonumber \]
Recordamos que la integral de superficie se define como positiva para un vector que apunta hacia afuera y negativa para uno que apunta hacia el volumen encerrado por la superficie. Ahora usamos la definición de la divergencia\[\begin{array}{l} \mathrm{div} (\mathbf{E}) &= \lim_{\Delta (V) \rightarrow 0} \frac{1}{\Delta (V)} \left(\oint\limits_{s,} E \ dS\right) \\ &= \lim_{\Delta (V) \rightarrow 0} \frac{\left(\mathbf{E} (x+\Delta (x)) - \mathbf{E}(x)\right) \Delta (y) \Delta (z)}{\Delta (x) \Delta (y) \Delta (z)} \\ &= \lim_{\Delta (V) \rightarrow 0} \frac{\mathrm{E} (x+\Delta(x)) - \mathrm{E}(x)}{\Delta (x)} \\ &= \frac{\delta \mathbf{E}(x)}{\delta x} \end{array} \nonumber \]
Entonces, tenemos para la forma diferencial de la ley de Gauss:\[\frac{\delta \mathbf{E}(x)}{\delta x} = \frac{\rho (x)}{\varepsilon} \nonumber \] Así, en nuestro caso, la tasa de cambio de\(E\) con\(x\)\(\dfrac{d}{dx} (E)\), o la pendiente de\(E(x)\) es apenas igual a la densidad de carga,\(\rho (x)\), dividida por\(\varepsilon\).


