3.4: Equilibrio entre los contactos y el conductor

En esta sección consideraremos la combinación de una molécula y un solo contacto.

En ausencia de una fuente de voltaje, el contacto aislado y la molécula están al mismo potencial. Así, sus energías de vacío (la energía potencial de un electrón libre) son idénticas en aislamiento. Cuando el contacto está conectado con la molécula, el equilibrio debe establecerse en el sistema combinado. Para evitar el flujo de corriente, debe haber una energía Fermi uniforme tanto en el contacto como en la molécula. Pero si las energías Fermi son diferentes en el contacto aislado y las moléculas, ¿cómo se obtiene el equilibrio?

Figura\(\PageIndex{1}\): La alineación energética de un contacto aislado y una molécula aislada. Si no hay fuente de voltaje en el sistema, la energía de un electrón libre es idéntica en las ubicaciones de contacto y molécula. Así, las energías de vacío se alinean. Las energías Fermi quizá no, sin embargo. Pero en equilibrio, las energías Fermi son forzadas a alinearse por transferencia de carga.

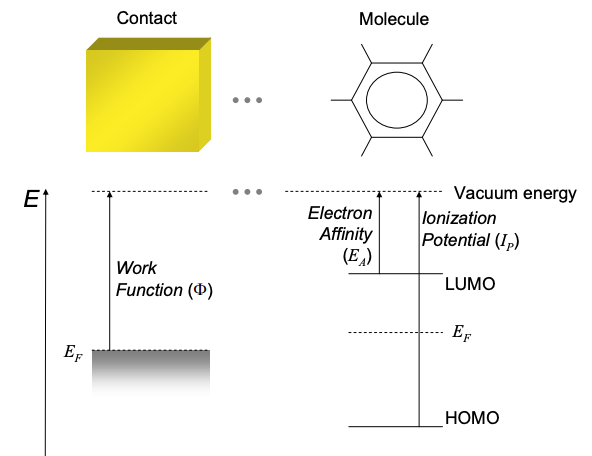
Dado que los niveles de Fermi cambian con la adición o resta de carga, el equilibrio se obtiene por transferencia de carga entre el contacto y la molécula. La transferencia de carga cambia el potencial del contacto con respecto a la molécula, desplazando las energías de vacío relativas. Esto se conoce como “carga”. La transferencia de carga también afecta los niveles de Fermi ya que los electrones llenan algunos estados y se vacían de otros. Tanto los efectos de carga como los de llenado de estado pueden ser modelados por capacitores. Consideraremos primero el llenado de estado electrónico.

La capacitancia cuántica

Figura\(\PageIndex{2}\): Una analogía para la transferencia de electrones en la interfaz entre un metal y una molécula. El tamaño del tanque de agua es equivalente a la densidad de los estados. El nivel de Fermi es equivalente al nivel del agua. Si el “metal” tiene una densidad suficientemente grande de estados, entonces el cambio en su nivel de agua es imperceptible.

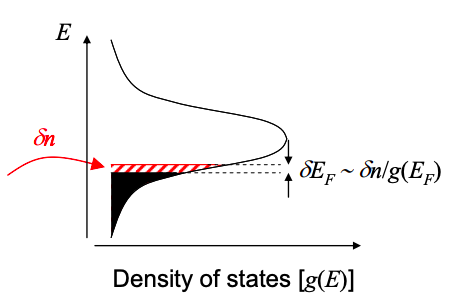
Pero una molécula no necesariamente tendrá una densidad uniforme de estados como se muestra en la Figura\(\PageIndex{2}\). También es posible que solo se transfiera una cantidad fraccionaria de carga. Por ejemplo, imagínese que algunos\(\delta n\) electrones de cantidad fraccional se transfieren del contacto a la molécula. Es posible que la función de onda del electrón transferido incluya tanto el contacto como la molécula. Dado que parte de la función de onda compartida reside en la molécula, esto es equivalente a una transferencia de carga fraccional.

Pero si\(\delta n\) fueran iguales a +1, la LUMO estaría medio llena y de ahí la energía Fermi estaría en la LUMO, mientras que si\(\delta n\) fueran -1, el HOMO estaría medio lleno y de ahí la energía Fermi estaría en el HOMO. En general, el número de cargas en la molécula viene dado por

\[ n=\int^{+\infty}_{-\infty} g(E)f(E,E_{F})dE \nonumber \]

donde g (E) es la densidad de estados moleculares por unidad de energía. Para pequeños cambios en la energía de Fermi, podemos linealizar la Ecuación (3.4.1) para determinar el efecto de la transferencia de carga sobre\(E_{F}\). Nos interesa la cantidad\(dE_{F}/dn\). Para sistemas degenerados podemos simplificar la Ecuación (3.4.1):

\[ n = \int^{E_{F}}_{-\infty}g(E)dE \nonumber \]

tomar la derivada con respecto a la energía Fermi da:

\[ \frac{dn}{dE_{F}} =g(E_{F}) \nonumber \]

Podemos reorganizar esto para obtener:

\[ \delta E_{F} = \frac{\delta n}{g(E_{F})} \nonumber \]

Así después de la transferencia de carga la energía Fermi dentro de la molécula cambia por\(\delta n/g\), donde g es la densidad de estados por unidad de energía.

A veces es conveniente modelar el efecto de llenar la densidad de estados por la “capacitancia cuántica” que definiremos como:

\[ C_{Q}=q^{2}g(E_{F}) \nonumber \]

i.e.

\[ \delta E_{F} = \frac{q^{2}}{C_{Q}}\delta n \nonumber \]

Si la molécula tiene una gran densidad de estados a nivel Fermi, su capacitancia cuántica es grande, y se debe transferir más carga para desplazar el nivel Fermi.

Figura\(\PageIndex{3}\): La transferencia de carga cambia el nivel de Fermi en un conductor. La magnitud del cambio está determinada por la densidad de estados a nivel Fermi, y a menudo se expresa en términos de una “capacitancia cuántica”.

También podemos calcular la capacitancia cuántica del contacto. Los contactos metálicos contienen una gran densidad de estados a nivel Fermi, lo que significa que se debe transferir un número muy grande de electrones para desplazar su nivel Fermi. Así, decimos que la energía Fermi del contacto está "clavada" por la densidad de los estados. Otra forma de expresar esto es que la capacitancia cuántica del contacto es aproximadamente infinita.

La capacitancia cuántica se puede emplear en un circuito equivalente para la unión metalmolécula. Pero hemos generalizado el circuito de tal manera que cada potencial de nodo es el nivel Fermi, no solo el potencial electrostático como en un circuito eléctrico convencional.

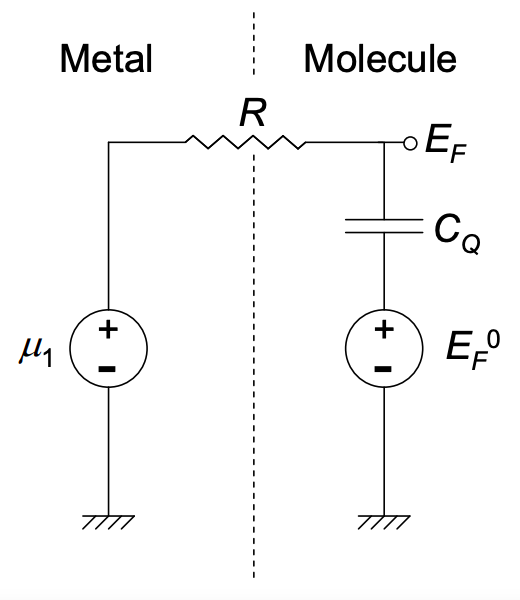
En el circuito de abajo, el metal es modelado por una fuente de voltaje igual al potencial químico\(\mu_{1}\) del metal. Previo al contacto, el nivel de Fermi de la molécula es\(E_{F}^{0}\). El contacto en sí está modelado por una resistencia que permite que la corriente fluya cuando los niveles de Fermi a ambos lados del contacto están desalineados. La carga que fluye del metal a la molécula desarrolla un potencial a través de la capacitancia cuántica. Pero tenga en cuenta que esto es un cambio en el nivel de Fermi, no un potencial electrostático. También es importante señalar que la capacitancia cuántica suele depender del nivel de Fermi en la molécula. La única excepción es si la densidad de estados es constante en función de la energía. Así, un valor constante de solo se\(C_{Q}\) puede emplear para pequeñas desviaciones entre\(\mu_{1}\) y\(E_{F}^{0}\).

Figura\(\PageIndex{4}\): Modelo de señal pequeña para la unión metal-molécula. Los efectos de la carga no están incluidos. La resistencia se caracterizará aún más en secciones posteriores.

Capacitancia electrostática

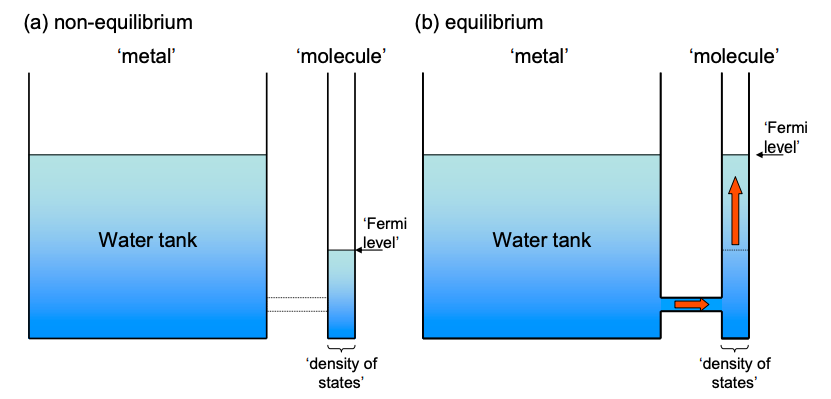
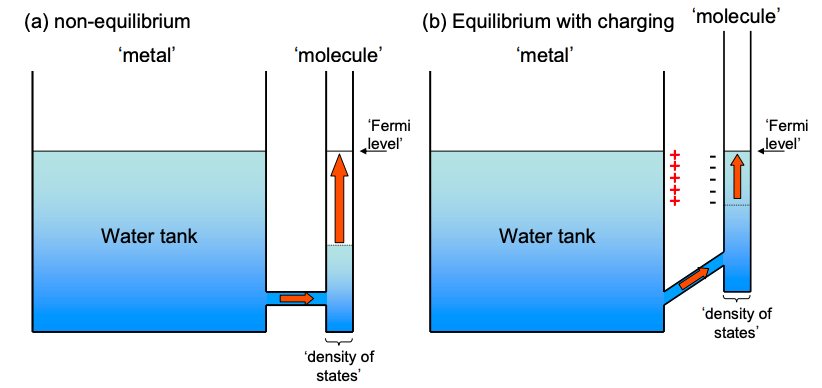
Desafortunadamente, el establecimiento del equilibrio entre un contacto y la molécula no es tan simple como el flujo de agua entre dos tanques. Los electrones, a diferencia del agua, están cargados. Así, la transferencia de electrones desde el contacto a una molécula deja una carga neta positiva en el contacto y una carga neta negativa en la molécula.

La carga en la interfaz cambia el potencial de la molécula en relación con el metal y es equivalente a desplazar todos los tanques de agua hacia arriba y hacia abajo. La carga ayuda al establecimiento del equilibrio y reduce el número de electrones que se transfieren después de que se realiza el contacto.

Figura\(\PageIndex{5}\): Los electrones transportan carga y desplazan el potencial cuando se transfieren entre un metal y una molécula. El cambio resultante en el potencial es equivalente a levantar la columna de “molécula” de agua. Los niveles de agua deben coincidir en última instancia, pero ahora se requiere menos agua para ser transferida.

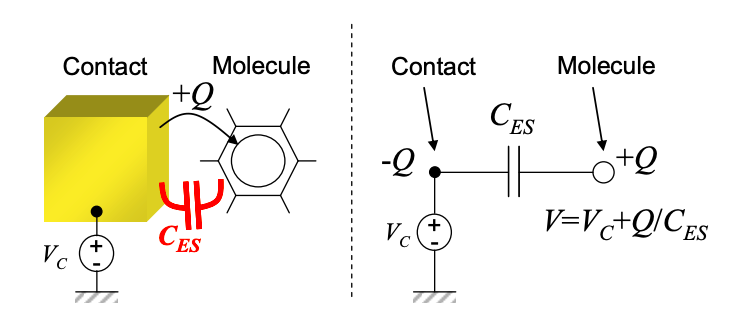
El contacto y la molécula pueden considerarse como las dos placas de un condensador. En la Figura 3.4.6 etiquetamos este condensador,\(C_{ES}\) - la capacitancia electrostática, para distinguirla de la capacitancia cuántica discutida en la sección anterior.

Cuando se transfiere carga en la interfaz, se carga el condensador, se establece un voltaje y la molécula cambia de potencial. El cambio en el potencial molecular por electrón transferido se conoce como la energía de carga y se refleja en un desplazamiento en la energía de vacío. De la relación fundamental para un condensador:

\[ C_{ES}=\frac{Q}{V} \nonumber \]

donde V es el voltaje a través del condensador. Podemos calcular el cambio de potencial debido al cobro:

\[ U_{C} = qV = \frac{q^{2}}{C_{ES}}\delta n \nonumber \]

Figura\(\PageIndex{6}\): Un contacto y una molécula se pueden modelar como dos placas de un condensador paralelo. Cuando se transfiere la carga, esta capacitancia electrostática determina el cambio en el potencial electrostático y, por lo tanto, el desplazamiento en la energía de vacío.

Encontraremos que\(\delta n\) es una cantidad dinámica — cambia con el flujo de corriente. Puede ser muy importante en nanodispositivos porque la capacitancia electrostática es muy pequeña. Para las pequeñas separaciones entre contacto y conductor típicas de la nanoelectrónica (por ejemplo, 1 nm), la energía de carga puede ser del orden de 1V por electrón.

Resumiendo estos efectos, encontramos que la energía Fermi de la molécula neutra,\(E_{F}^{0}\), está relacionada con la energía Fermi de la combinación metal-molécula,\(E_{F}\), por

\[ E_{F} = \delta n/g +\frac{q^{2}}{C_{ES}}\delta n +E_{F}^{0} \nonumber \]

Figura\(\PageIndex{7}\): Modelo de señal pequeña para la unión metal-molécula, incluyendo los efectos de la carga. La resistencia se caracterizará aún más en secciones posteriores.

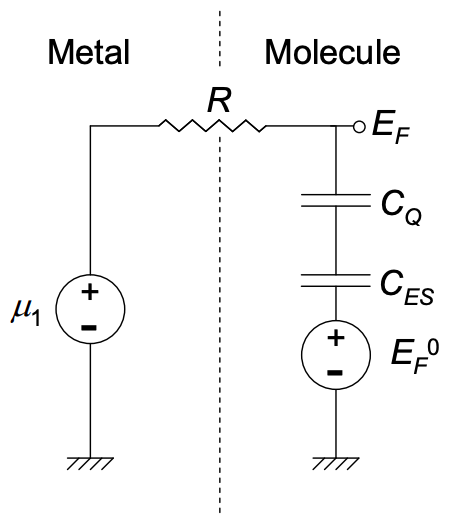
O, en términos de la capacitancia cuántica:

\[ E_{F} = \frac{q^{2}}{C_{Q}} \delta n + \frac{q^{2}}{C_{ES}} \delta n + E_{F}^{0} \nonumber \]

Figura\(\PageIndex{8}\): Cambios en la alineación del nivel de energía cuando la carga se transfiere del metal a una molécula. La carga de la molécula corresponde a aplicar un voltaje a través de un condensador interfacial, cambiando así el potencial de la molécula. En consecuencia, el nivel de vacío se desplaza en la ubicación de la molécula, desplazando todos los estados moleculares junto con ella. Además, la carga transferida llena algunos estados vacíos previos en la molécula. Ambos efectos cambian la energía de Fermi en la molécula.