4.6: El límite cuántico de la conductancia
- Page ID
- 84573
Hemos visto que en un cable cuántico, el flujo de corriente requiere una diferencia en los niveles cuasi de Fermi para los electrones que se mueven con y contra la corriente. Además, solo los electrones entre los cuasi niveles de Fermi, es decir,\(F^{-}<E<F^{+}\) llevan corriente.
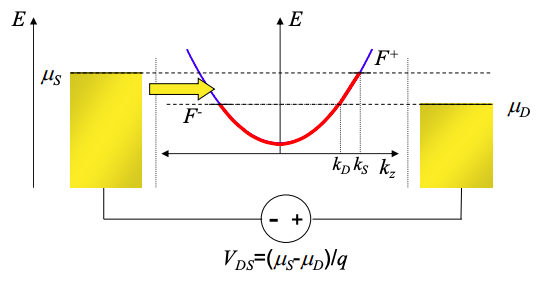
En general, la corriente total en un cable cuántico es
\[ I = qN/\tau \nonumber \]
donde N es el número de electrones no compensados, y\(\tau\) es su tiempo de tránsito (el tiempo que tardan en cruzar de un extremo del cable al otro). Vamos a usar la Ecuación (4.6.1) para calcular la corriente en un cable cuántico de modo único a T=0K.
La velocidad de los electrones en el cable viene dada por la velocidad del grupo (ver Problema 3)
\[ v = \frac{1}{\hbar}\frac{dE}{dk} \nonumber \]
Como un aparte, observamos que si\(F^{+}-F^{-}\) es pequeña, la corriente que transporta electrones se mueven aproximadamente a la velocidad de Fermi en equilibrio.
\[ v_{F}=\left.\frac{1}{\hbar} \frac{d E}{d k}\right|_{E_{F}} \nonumber \]
El tiempo de tránsito en la Ecuación (4.6.1) está relacionado con la longitud del cable, L, y la velocidad de los electrones no compensados:
\[ \tau = \frac{L}{v} = L / \left( \frac{1}{\hbar} \frac{dE}{dk}\right) \nonumber \]
El número de electrones no compensados es igual al número de electrones en los estados\(k_{D} < k < k_{S}\), equivalente a\(\mu_{D} < E < \mu_{S}\) en la Figura 4.6.1. Cada k estado ocupa\(\Delta k = 2\pi / L\). Recordemos también que hay dos electrones por k estado (uno de cada espín). Por lo tanto,
\[ N = 2 \int^{k_{S}}_{k_{D}} \frac{dk}{2\pi / L} \nonumber \]
La ecuación (4.6.1) es entonces
\[ I = 2q \int^{k_{S}}_{k_{D}} \frac{dk}{2\pi /L} \frac{1}{h L}\frac{dE}{dk} \nonumber \]
Simplificando da
\[ I = \frac{2q}{h} \int^{k_{S}}_{k_{D}} dk\ \frac{dE}{dk} \nonumber \]
Cambiar la variable de integración a energía da
\[ I = \frac{2q}{h} \int^{\mu_{S}}_{\mu_{D}} dE \nonumber \]
\( =\frac{2q}{h} (\mu_{S}-\mu_{D}) \)
Tenga en cuenta\(V_{DS} = -(\mu_{D}-\mu_{S})/q\), así
\[ I=\frac{2q^{2}}{h} V \nonumber \]
Esta expresión demuestra que la resistencia de un cable monomodo ideal es
\[ R = \frac{h}{2q^{2}} \approx 12.9\ k\Omega \nonumber \]
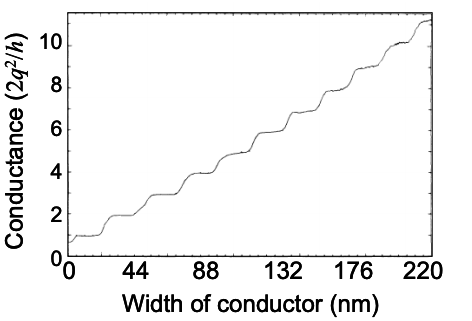
Un cable de modo múltiple con modos M se puede considerar como M cables monomodo en paralelo. Dado que las conductancias paralelas se suman, el límite cuántico suele escribirse como una conductancia. Para un cable balístico multimodo, la conductancia es
\[ G_{C} = \frac{2q^{2}}{h}\ M \nonumber \]
Esta es la famosa conductancia cuántica limitada. Se obtiene la sorprendente conclusión de que incluso los conductores balísticos tienen una resistencia, aunque esta resistencia es independiente de la longitud del conductor.
Pero una resistencia implica que el poder se disipa cuando fluye una corriente. Dado que el transporte de electrones en el cable es balístico, ¿dónde ocurren las pérdidas de potencia resistiva?
Si observamos la Figura 4.6.1 encontramos que los portadores que ingresan al cable desde la fuente se propagan sin cambio de potencial hasta llegar al drenaje donde deben llegar al equilibrio a potencial químico\(\mu_{D}\). Así, la potencia se disipa en el desagüe.
El límite cuántico en la conductancia surge como consecuencia de la interfaz entre el contacto con sus (idealmente) modos infinitos y número infinito de electrones todos en equilibrio, y un conductor con un pequeño número de modos que soportan electrones no equilibrados. Así, el límite cuántico se puede considerar como una resistencia de contacto.
Por supuesto, a medida que aumenta el número de modos en el conductor, la resistencia de contacto disminuye. En el límite clásico, puede ser ignorado por completo.