5.4: Capacitancia cuántica en FET

Última actualización
Guardar como PDF

Page ID: 84220

Marc Baldo
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Desafortunadamente, las Ecuaciones. (5.3.4) y (5.3.5) normalmente deben resolverse iterativamente. Pero se puede obtener perspicacia estudiando un FET con algunas aproximaciones.

Otra forma de pensar sobre el cobro es considerar el efecto sobre el potencial del canal de los cambios incrementales en\(V_{GS}\) o\(V_{DS}\). Luego podemos aplicar modelos de capacitores simples de carga de canal para determinar el potencial de canal en la Ecuación (5.3.6).

Si el potencial en el canal cambia\(\delta U\) entonces el número de cargos en el canal cambia en

\[ \delta N = -g(E_{F})\delta U \nonumber \]

Tenga en cuenta que hemos asumido T = 0K, y anotar también el signo negativo — hacer que el potencial del canal sea más negativo aumenta el número de cargos.

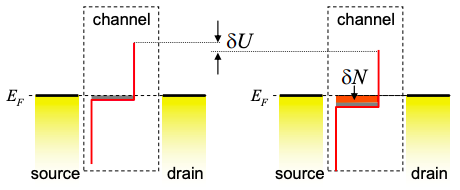
Captura de pantalla 2021-05-18 a las 17.51.33.png — Figura\(\PageIndex{1}\): Un cambio en el potencial del canal cambia el número de cargas en el canal.

Sustituir de nuevo a la Ecuación (5.3.4) da

\[ \delta U = -q \delta V_{GS} \frac{C_{G}}{C_{ES}}-q \delta V_{DS} \frac{C_{D}}{C_{ES}}-\frac{q^{2}}{C_{ES}}g(E_{F})\delta U \nonumber \]

Recopilación\(\delta U\) de términos da

\[ \delta U = -q \delta V_{GS} \frac{C_{G}}{C_{ES} +C_{Q}}-q \delta V_{DS} \frac{C_{D}}{C_{ES}+C_{Q}} \nonumber \]

Donde recordamos la capacitancia cuántica (\(C_{Q}\)):

\[ C_{Q}=q^{2}g(E_{F}) \nonumber \]

Usando la capacitancia cuántica, podemos construir fácilmente un modelo de señal pequeña para cambios en\(V_{GS}\) o\(V_{DS}\). Véase, por ejemplo, el\(V_{GS}\) modelo de señal pequeña en la Figura 5.4.2. Tenga en cuenta que el valor de la capacitancia cuántica depende del potencial del canal en el punto de polarización.

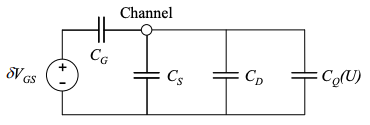
Captura de pantalla 2021-05-18 a las 17.56.12.png — Figura\(\PageIndex{2}\): Un modelo de señal pequeña para el potencial de canal.

Usando la Ecuación (5.4.1) también podemos determinar un modelo de señal pequeña para la carga en el canal.

\[ q\delta N=\delta V_{GS} \frac{C_{G}C_{Q}}{C_{ES}+C_{Q}} \nonumber \]

En la siguiente sección consideraremos la operación de FET bajo dos casos limitantes: (i) cuando\(C_{Q}\) es grande relativo a\(C_{ES}\), y (ii) cuando\(C_{Q}\) es pequeño. Los dos casos corresponden típicamente a los estados ON y OFF de un FET, respectivamente.