5.8: La dependencia de la temperatura de la corriente en el estado OFF
- Page ID
- 84258
Tanto los transistores a nanoescala como los más grandes tienen una pequeña capacitancia cuántica en el estado OFF, que también se conoce como subumbral desde entonces\(V_{GS} < V_{T}\).
Pero aunque la densidad de estados sea cero entre\(\mu_{S} > E > \mu_{D}\), a temperaturas más altas, algunos electrones pueden ser excitados en estados vacíos muy por encima de la Energía Fermi. Si la densidad de estados es muy baja en la Energía Fermi, pero mayor lejos del nivel Fermi, entonces podemos modelar la distribución de Fermi por una cola exponencial. Recordemos que esto se conoce como una distribución no degenerada; ver Figura 5.8.1.
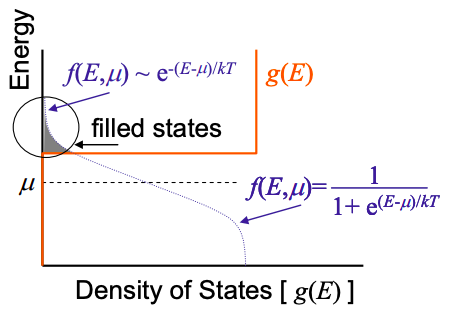
La ecuación (5.5.3) se convierte
\[ N_{S} = \int^{\infty}_{-\infty} g(E-U)e^{-(E-\mu_{S})/kT}dE \nonumber \]
Ahora cambiando la variable de integración a\(E’=E-U\)
\[ N_{S} = \int^{\infty}_{-\infty} g(E’)e^{-(E’+U-\mu_{S})/kT}dE’ \nonumber \]
Simplificando
\[ N_{S} = e^{-U/kT}\int^{\infty}_{-\infty} g(E’)e^{-(E’-\mu_{S})/kT}dE’ \nonumber \]
Del mismo modo,
\[ N_{D} = e^{-U/kT}\int^{\infty}_{-\infty} g(E’)e^{-(E’-\mu_{D})/kT}dE’ \nonumber \]
Así, a partir de la Ec. (5.5.3) la corriente es
\[ I = \frac{q}{\tau}\text{exp}\left[\frac{qV_{GS}}{kT} \right] \cdot \int^{\infty}_{-\infty} g(E’)\left( e^{-(E’-\mu_{S})/kT} - e^{-(E’-\mu_{D})/kT}\right) \nonumber \]
Ecuación (5.8.5) mantiene en el límite que\(C_{G} \gg C_{S}, C_{D}\). En general, encontramos que la corriente en la región subumbral es
\[ I = I_{0}\text{exp}\left[\frac{qV_{GS}}{kT} \frac{C_{G}}{C_{ES}}\right] \nonumber \]
Tomando logaritmo de ambos lados encontramos,
\[ \text{log}_{10}I=\frac{q}{KT}\frac{C_{G}}{C_{ES}}(\text{log}_{10}e)V_{GS}+\text{log}_{10}I_{0} \nonumber \]
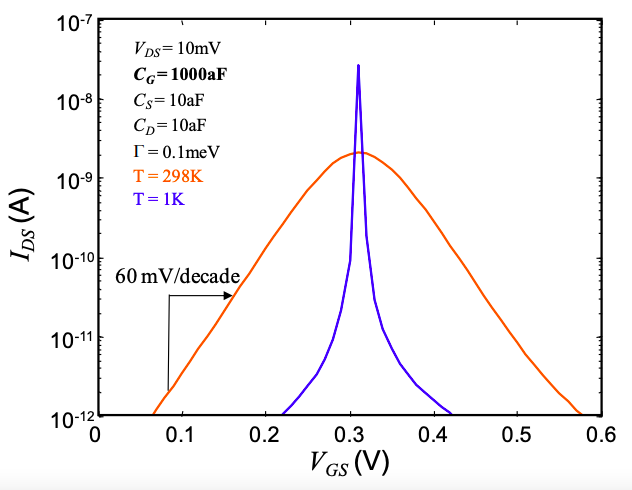
La pendiente, S, del régimen subumbral suele expresarse en voltios de puerta por década de corriente de drenaje. A temperatura ambiente, el óptimo, cuando\(C_{G} \gg C_{S}, C_{D}\), es
\[ S=\frac{kT}{q}\frac{1}{\text{log}_{10}e} \approx 60 \text{ mV/decade} \nonumber \]
La pendiente se vuelve mucho más aguda a bajas temperaturas; ver Figura 5.8.2.