5.10: El FET de Alambre Cuántico Balístico

Última actualización
Guardar como PDF

Page ID: 84193

Marc Baldo
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Considere el FET de alambre cuántico balístico que se muestra en la Figura 5.10.1.

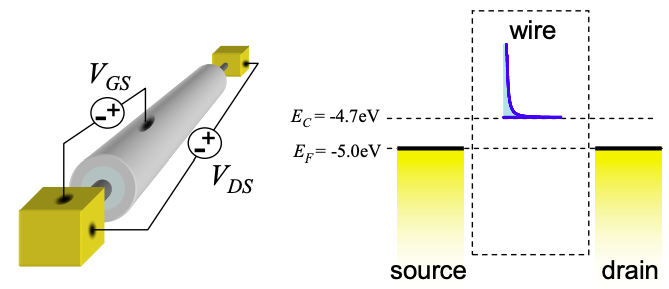
Captura de pantalla 2021-05-18 a las 19.06.20.png — Figura\(\PageIndex{1}\): Un FET de alambre cuántico. La puerta se envuelve alrededor del cable para maximizar la capacitancia entre el canal y la puerta. La longitud del cable es L = 100nm, la capacitancia de la puerta es\(C_{G}\) = 50 aF por nanómetro de longitud del cable, y la masa de electrones, m, en el cable es\(m=m_{0}=9.1\times10^{-31} kg\).

Supondremos que solo hay una banda parabólica en el cable.

De la Ecuación (2.10.6), la densidad de estados en el cable es:

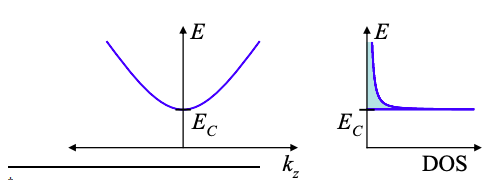
Captura de pantalla 2021-05-18 a las 19.10.38.png — Figura\(\PageIndex{2}\): Estructura de banda y densidad de estados en un cable cuántico monomodo.

\[ g(E)dE=\frac{2L}{h}\sqrt{\frac{2m}{E-E_{C}}}u(E-E_{C})dE , \nonumber \]

donde L es la longitud del cable, y m es la masa de electrones en el alambre. Pero sólo la mitad de estos estados contienen electrones que viajan en la dirección positiva. Por lo tanto, debemos dividir la Ecuación (5.10.1) por dos para producir:

\[ g^{+}(E)dE=\frac{1}{2}\times\frac{2L}{h}\sqrt{\frac{2m}{E-E_{C}}}u(E-E_{C})dE \nonumber \]

Dada la posición de la Fermi Energy, esta banda es la banda de conducción. Vamos a etiquetar la energía en la parte inferior de la banda de conducción,\(E_{C}\). Ya que modelamos electrones que se mueven a lo largo del cable como ondas planas, dentro de la banda parabólica tenemos

\[ E-E_{C} =\frac{\hbar^{2}k^{2}}{2m} = \frac{1}{2}mv^{2} \nonumber \]

Podemos reescribir la Ecuación (5.10.2) en términos de la velocidad, v, del electrón:

\[ g^{+}(E)dE = \frac{1}{2}\times \frac{4L}{hv(E)}u(E-E_{C})dE \nonumber \]

Ahora L/v es el tiempo de tránsito de un electrón a través del cable, así

\[ g^{+}(E)dE = \frac{1}{2}\times \frac{4\tau(E)}{h}u(E-E_{C})dE \nonumber \]

Podemos sustituir la ecuación (5.10.5) en la expresión para la densidad de corriente (Ecuación (5.9.4)) para obtener

\[ I= \frac{2q}{h}\int^{+\infty}_{-\infty} u(E-E_{C}-U)(f(E,\mu_{S})-(f(E,\mu_{D}))dE . \nonumber \]

\(^{†}\)Este análisis del FET de alambre cuántico balístico me lo presentó Mark Lundstrom en la Universidad de Purdue. Para una referencia completa, consulte Mark Lundstrom y Jing Guo, “Transistores a nanoescala: física, modelado y simulación”, Springer, Nueva York, 2006.