6.7: Ejemplos de cálculos de encuadernación ajustada

Consideremos un conductor que consta de cuatro átomos, cada uno de los cuales proporciona un orbital atómico fronterizo que contiene un solo electrón. Un equivalente molecular a este conductor modelo es 1,3-butadieno; ver Figura 6.8.1. Aquí cada átomo de carbono aporta un electrón en un orbital atómico fronterizo.

Figura\(\PageIndex{1}\): (izquierda) Un conductor modelo de cuatro átomos, donde cada átomo aporta un solo electrón en una órbita atómica fronteriza. (derecha) Un equivalente químico aproximado es 1,3-butadieno, donde los átomos de carbono proporcionan los orbitales fronterizos.

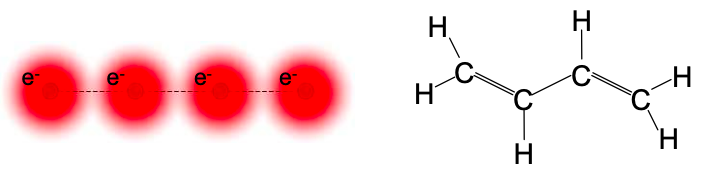
Ignoraremos los átomos de hidrógeno, ya que los electrones fronterizos son donados por los átomos de carbono. Etiquetemos los cuatro orbitales atómicos de la frontera de carbono\(\phi_{1}, \phi_{2}, \phi_{3},\text{ and } \phi_{4}\).

Siguiendo la Ecuación (6.4.1), dejamos que los orbitales moleculares sean

\[ \psi = c_{1}\phi_{1}+c_{2}\phi_{2}+c_{3}\phi_{3}+c_{4}\phi_{4} \nonumber \]

donde aún no se han determinado los\(c_i\) coeficientes.

Consideremos a continuación las integrales de la forma:

\[ \left< \phi_{m}|H|\psi \right> = \left< \phi_{m}|E|\psi \right> = E \left< \phi_{m}|\psi \right> \nonumber \]

Considerando\(m = 1\)\(m=2\),\(m=3\) y\(m=4\) a su vez, obtenemos cuatro ecuaciones:

\ [\ comenzar {alinear*}\ izquierda<\ phi_ {1} |H|\ psi\ right> &= c_ {1}\ alfa_ {1} + c_ {2}\ beta_ {12} = c_ {1} E\\ [4pt]
\ izquierda<\ phi_ {2} |H|\ psi\ right> &= c_ {2}\ alpha_ {2} + c_ {1}\ beta_ {21} +c_ {3}\ beta_ {23} = c_ {2} E\\ [4pt]
\ izquierda<\ phi_ {3} |H|\ psi\ right> &= c_ {3}\ alfa_ {3} + c_ {2}\ beta_ {32} +c_ {4}\ beta_ {34} = c_ {3} E\\ [4pt]
\ izquierda<\ phi_ {4} |H|\ psi\ right> &= c_ {4}\ alpha_ {4} + c_ {3}\ beta_ {43} = c_ {4} E\ end {align*}\ nonumber\]

Se puede pensar en cada ecuación como una descripción de las interacciones entre un átomo de carbono en particular, y él mismo y sus vecinos. Resolver estas ecuaciones da los coeficientes\(c_{1}, c_{2}, c_{3}, \text{ and } c_{4}\). Para simplificar, asumiremos que la autoenergía en cada átomo de carbono es la misma, i.e.

\[ \alpha = \alpha_{1} = \alpha_{2}= \alpha_{3}= \alpha_{4} \nonumber \]

Además, asumiremos que las interacciones de salto entre los átomos de carbono vecinos son las mismas, i.e.

\[ \beta = \beta_{12} =\beta_{21} =\beta_{23} =\beta_{32}=\beta_{34}=\beta_{43} \nonumber \]

Quizás la mejor manera de resolver las ecuaciones sistemáticamente es a través de una matriz. Las ecuaciones se pueden reescribir:

\ [\ left (\ begin {array} {cccc}
\ alpha &\ beta & 0 & 0\\
\ beta &\ alpha &\ beta &\ alpha &\ beta &
0\\ 0 &\ beta &\ alpha &\
beta\ 0 &\ beta &\ alpha
\ end {array}\ derecha)\ left (\ begin {array} {l}
c_ {1}\\
c_ {2}\
c_ {3}\\
c_ {4}
\ end {array}\ derecha) =E\ izquierda (\ begin {array} {l}
c_ {1}\\
c_ {2}\\
c_ {3}\\
c_ {4}
\ end {array}\ derecha)\ nonumber\]

Esta ecuación es de la forma familiar

\[ H| \psi \big \rangle = E| \psi \big \rangle \nonumber \]

donde el hamiltoniano está en forma de matriz, y la función de onda es un vector de columna que contiene los coeficientes que ponderan los orbitales atómicos:

\ [H=\ izquierda (\ begin {array} {cccc}
\ alpha &\ beta & 0 & 0\\
\ beta &\ alpha &\ alpha &\ beta &
0\\ 0 &\ beta &\ alpha &\ beta &\
beta\ 0 &\ beta &\ alpha
\ end {array}\ derecha),\ quad\ psi=\ left (\ begin {array} { l}
c_ {1}\\
c_ {2}\\
c_ {3}\\
c_ {4}
\ end {array}\ derecha)\ nonumber\]

Expresar la función hamiltoniana y ondulada en esta forma es un ejemplo de mecánica matricial, una versión de la mecánica cuántica formulada por Werner Heisenberg que resulta conveniente para muchos problemas. Aparte de este ejemplo, no vamos a perseguir la mecánica matricial en esta clase.

Pero vale la pena tomarse un momento para examinar la estructura de la matriz hamiltoniana. Cada fila describe ahora las interacciones entre orbitales fronterizos sobre un átomo de carbono, y ella misma y sus vecinos. La diagonal de la matriz contiene las autoenergías, y los elementos offdiagonal son las interacciones de salto. Este ejemplo particular es tridiagonal, es decir, los elementos de la matriz son cero, excepto la diagonal, y sus elementos de matriz inmediatamente adyacentes. Las moléculas lineales con enlaces simples y dobles alternantes siempre poseen matrices tridiagonales.

Después de un poco de práctica con cálculos de encuadernación apretada deberías poder saltar directamente a anotar la matriz hamiltoniana. Por ejemplo, considere el ciclobutadieno; se muestra a continuación.

Figura\(\PageIndex{2}\): Una molécula cíclica de cuatro átomos y su equivalente químico, ciclobutadieno.

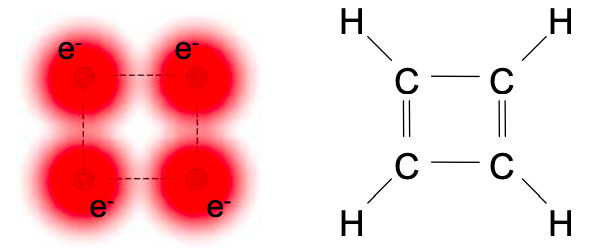
Debido a su estructura de anillo, el ciclobutadieno tiene interacciones de salto adicionales entre los carbonos #1 y #4 que estaban en los extremos de la cadena en 1,3-butadieno. Estas interacciones en las posiciones 1,4 y 4,1 están marcadas en rojo en la Ecuación (6.8.9) a continuación

\ [H=\ left (\ begin {array} {cccc}
\ alpha &\ beta & 0 &\ textcolor {rojo} {\ beta}\\ beta &
\ alpha &\ beta & 0\\ 0 &\
beta &\ alpha &\ alpha &\ beta &\ beta
\\ textcolor {rojo} {\ beta} & 0 &\ beta &\ alpha
\ end { array}\ derecha)\ nonumber\]

Como probablemente puedas imaginar, para todas menos las moléculas más simples, estas matrices pueden llegar a ser extremadamente grandes y difíciles de usar. Y resolverlos puede ser extremadamente intensivo desde el punto de vista computacional. De hecho, los cálculos de encuadernación apretada casi nunca se hacen a mano. Pero se puede obtener alguna idea resolviendo analíticamente moléculas lineales simples.

Volviendo al 1,3-butadieno, reordenando la Ecuación (6.8.6), obtenemos:

\ [\ left (\ begin {array} {cccc}
\ alfa-E &\ beta & 0 & 0\\ beta &
\\ beta &\ alfa-E &\ beta &
0\\ 0 &\ beta &\ alfa-E &\ beta\\
0 & 0 &\ beta &\ alpha-E
\ end {array}\ derecha)\ left (\ begin {array} {l}
c_ {1}\\
c_ {2}\\
c_ {3}\\
c_ {4}
\ end {array}\ derecha) = 0\ nonumber\]

Para encontrar la solución no trivial (es decir, soluciones distintas a\(c_{1} = c_{2} = c_{3} = c_{4} =0\)) tomamos el determinante:

\ [\ izquierda|\ begin {array} {cccc}
\ alfa-E &\ beta & 0 & 0\\ beta &
\\ beta &\ alfa-E &\ beta &\ beta &
0\\ 0 &\ beta &\ alfa-E &\ beta\\
0 &\ beta &\ alpha-E
\ end {array}\ derecha|=0\ nonumber\]

Las soluciones son:

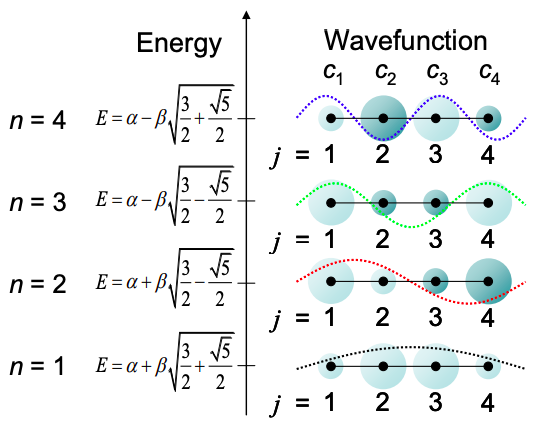
\[E = \alpha \pm \beta\sqrt{\frac{3}{2}\pm\frac{\sqrt{5}}{2}} \nonumber \]

Y las funciones propias son:

\[ c_{j} = sin\left(\ jn \frac{\pi}{5} \right), \ \ j,n=1,2,3,4 \nonumber \]

Estas soluciones se resumen en la Figura\(\PageIndex{3}\). Los orbitales moleculares son similares a las ondas estacionarias esperadas para una partícula en una caja.

Figura\(\PageIndex{3}\): Los orbitales moleculares y sus energías para 1,3-butadieno. Después de “Molecular Quantum Mechanics”, de Atkins y Friedman, 3a edición, Cambridge University Press, 1997.