7.5: Computadoras reversibles

En la sección anterior, definimos el cómputo como un proceso que incrementa la información y disminuye la incertidumbre. Pero si la incertidumbre (es decir, la entropía) disminuye dentro de la computadora, la entropía debe aumentar fuera de la computadora. Se trata de una aplicación de la segunda ley de la termodinámica, que establece que todos los sistemas físicos sólo pueden incrementar la entropía con el tiempo.

De todas las leyes físicas, la segunda ley de la termodinámica es famosa por definir la “flecha del tiempo”. La implicación de la segunda ley es que la computación es irreversible, al menos si la computación cambia la incertidumbre.

Por ejemplo, consideremos una puerta AND de dos entradas. Si una de las entradas a la puerta AND es un cero, entonces la información en la otra entrada es desechada. Así, el número total de estados disminuye cuando las entradas se propagan a la salida de una puerta AND. En consecuencia, la entropía disminuye, el calor se disipa y las puertas AND no son reversibles.

Figura\(\PageIndex{1}\): Las puertas Y no son reversibles. Si la salida es cero, las entradas no pueden ser reconstruidas.

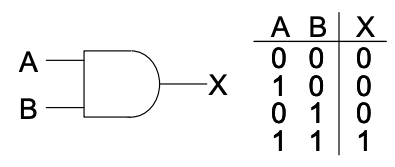
El calor disipado en la puerta AND se calcula de la siguiente manera. Hay cuatro posibles estados de entrada. Suponiendo que cada uno es equiprobable, la entropía de Shannon es

\[ H_{in} = -\log_{2} 1/4 = 2 \text{ bits} \nonumber \]

Hay dos estados de salida posibles. La probabilidad de la salida X = 0 es ¾ y la probabilidad de X = 1 es ¼.

\[ H_{out} = -\frac{3}{4} \log_{2} 3/4 - \frac{1}{4}\log_{2}1/4 \approx 0.811 \text{ bits} \nonumber \]

Por lo tanto,

\[ \Delta E = -k_{B} T\ln(2)\Delta H \approx 3.4\times 10^{-21} J \nonumber \]

Pero, ¿y si diseñamos una puerta que no tirara a la basura los estados durante el cómputo? Tal sistema sería reversible, y lo que es más importante, no necesitaría disipar la energía.

De hecho, se han propuesto varios elementos lógicos reversibles. Quizás la computadora irreversible más conocida es la computadora de bola de billar pionera por Fredkin.

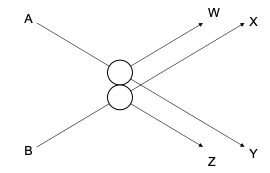
Un ejemplo de una puerta lógica de bola de billar se muestra en la Figura\(\PageIndex{2}\). Las bolas de billar se disparan hacia la puerta lógica desde las posiciones A y B. Si hay una colisión, las bolas se desvían a las posiciones W y Z. Si una bola está ausente, sin embargo, se genera una salida en X o Y. También hay que asumir que las bolas obedecen las leyes de la mecánica clásica; no hay fricción y las colisiones son perfectamente elásticas. Tenga en cuenta que el número de estados en una bola de billar elementos lógicos no cambia — las bolas de billar no se crean ni se destruyen.

Figura\(\PageIndex{2}\): Una puerta de colisión de dos bolas. Después de Feynman, Conferencias sobre Computación. Editores A.J.G. Hola y R.W. Allen, Addison-Wesley 1996.

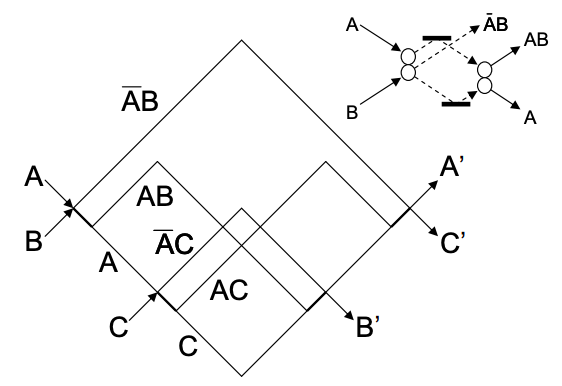
Los dispositivos más complejos son posibles añadiendo “puertas de redirección” (muros). Por ejemplo, la Figura\(\PageIndex{3}\) muestra un interruptor hecho a partir de puertas de colisión y redirección.

Figura\(\PageIndex{3}\): Un interruptor de bola de billar. Después de Feynman, Conferencias sobre Computación. Editores A.J.G. Hola y R.W. Allen, Addison-Wesley 1996.

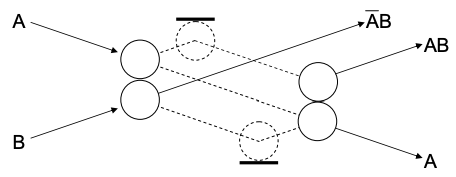
Pero dado que muchas puertas lógicas como la puerta AND son inherentemente no reversibles, surge la pregunta: ¿Se puede implementar un algoritmo arbitrario enteramente a partir de elementos reversibles? La respuesta es sí. Las computadoras reversibles pueden construirse completamente de un elemento reversible fundamental conocido como la puerta Fredkin, que se muestra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{4}\): El símbolo de la puerta de Fredkin. A no ha cambiado. Si A = 0 entonces B y C cambian. Si A = 1 entonces B y C permanecen sin cambios. Todos los elementos lógicos pueden formularse a partir de puertas reversibles de Fredkin. Después de Feynman, Conferencias sobre Computación. Editores A.J.G. Hola y R.W. Allen, Addison-Wesley 1996.

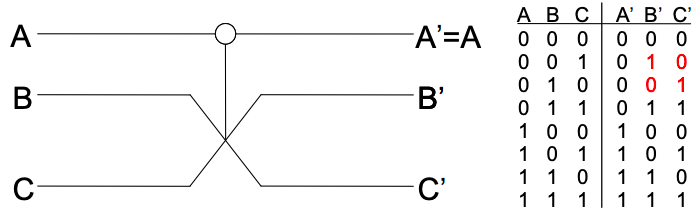
En la Figura se muestra una implementación de una puerta Fredkin con bolas de billar\(\PageIndex{4}\).

Figura\(\PageIndex{5}\): Una puerta Fredkin construida a partir de cuatro interruptores de bola de billar. Después de Feynman, Conferencias sobre Computación. Editores A.J.G. Hola y R.W. Allen, Addison-Wesley 1996.