8.5: Apéndice 4 - Orbitales Híbridos
- Page ID
- 84331
Alineación lineal con dos vecinos (hibridación sp)
Considera tres átomos en una línea, como se muestra en la Figura\(\PageIndex{1}\). Arbitrariamente alineamos los átomos con el eje x.
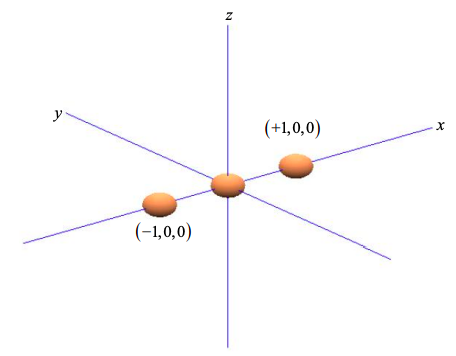
Deseamos determinar la contribución de los orbitales del átomo central a los\(\sigma\) enlaces. Recordemos que\(\sigma\) los enlaces tienen densidad electrónica en el eje entre los átomos.
Ahora bien, si el conjunto de bases consiste en orbitales s y p, solo\(s\) y\(p_{x}\) orbitales pueden contribuir a\(\sigma\) enlaces en el eje x. \(p_{y}\)y\(p_{z}\) los orbitales tienen densidad cero en el eje x y por lo tanto no pueden contribuir a los\(\sigma\) enlaces. Sin embargo, pueden contribuir a\(\pi\) los vínculos.
Definamos los orbitales atómicos adaptados a simetría que contribuyen a\(\sigma\) los enlaces generalmente como:
\[ \phi_{\sigma}=c_{s}\phi_{s}+c_{p_{z}}\phi_{p_{z}} \label{8.5.1} \]
donde\(c_{s}\) y\(c_{p_{x}}\) son los coeficientes de ponderación para los\(s\) y\(p_{x}\) orbitales respectivamente. Hay dos\(\sigma\) lazos: uno a la izquierda y otro a la derecha. Vamos a definir los dos orbitales atómicos adaptados a simetría que contribuyen a estos\(\sigma\) enlaces como\(\phi_{\sigma}^{1}\) y\(\phi_{\sigma}^{2}\) respectivamente.
La órbita s contribuye igualmente a ambos orbitales atómicos adaptados a la simetría. i.e.
\[ |c_{s}|^{2} = \frac{1}{2},\ \ \ c_{s} =\frac{1}{\sqrt{2}} \label{8.5.2} \]
Dado que el\(p_{x}\) orbital está alineado con el eje x, podemos ponderar los componentes\(p_{x}\) orbitales por las coordenadas de los dos átomos vecinos en x = +1 y x = -1,
\ [\ phi_ {\ sigma} ^ {1} = c_ {s}\ phi_ {s} + c_ {p}\ phi_ {p_ {x}}\
\ phi_ {\ sigma} ^ {2} = c_ {s}\ phi_ {s} - c_ {p}\ phi_ {p_ {x}}\ etiqueta {8.5.3}\]
En la primera orbital, estamos sumando los s y\(p_{x}\) orbitales en fase. En consecuencia, tenemos la densidad máxima de electrones en la dirección x positiva. En el segundo, estamos sumando los s y\(p_{x}\) orbitales fuera de fase, produciendo una densidad máxima de electrones en la dirección x negativa.
La normalización de cada orbital da
\[ |c_{p}|^{2} = \frac{1}{2},\ \ \ c_{p} =\sqrt{\frac{1}{2}} \label{8.5.4} \]
Así, el primer orbital atómico adaptado a simetría es
\[ \phi_{\sigma}^{1} = \frac{1}{\sqrt{2}}(\phi_{s}+\phi_{p_{x}}) \label{8.5.5} \]
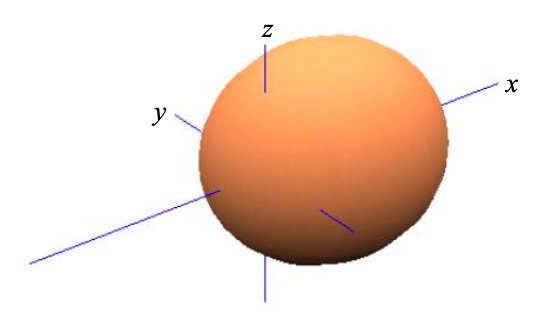
Del mismo modo, el segundo orbital atómico adaptado a simetría es
\[ \phi_{\sigma}^{2} = \frac{1}{\sqrt{2}}(\phi_{s}-\phi_{p_{x}}) \label{8.5.6}. \]
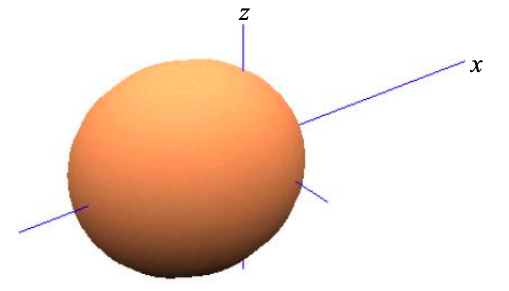
Así, basado puramente en argumentos de simetría, en una cadena lineal de átomos es conveniente reexpresar los cuatro orbitales atómicos s,\(p_{x}\),\(p_{y}\) y\(p_{z}\), como
\[ \phi_{\sigma} = \frac{1}{\sqrt{2}}(\phi_{s} \pm\phi_{p_{x}}) \label{8.5.7}, \]
donde\(p_{y}\) y no\(p_{z}\) se vean afectados. Esto se conoce como hibridación sp ya que hemos combinado uno s orbital atómico, y uno p orbital atómico para crear dos orbitales atómicos que contribuyen a los\(\sigma\) enlaces.
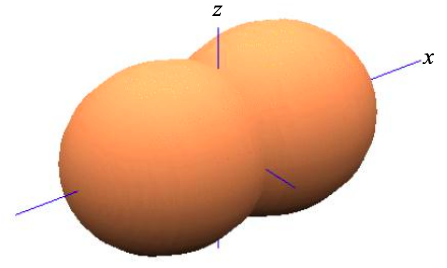
Los orbitales restantes\(p_{y}\) y\(p_{z}\) atómicos pueden combinarse en orbitales moleculares con mayor energía. El orbital molecular más alto ocupado (HOMO) también se conoce como orbital molecular fronterizo. En un material hibridado sp, el orbital molecular fronterizo será una combinación lineal de orbitales\(p_{z}\) atómicos\(p_{y}\) y orbitales. El orbital molecular fronterizo es relevante para nosotros, porque es más probable que los niveles más profundos se llene parcialmente. En consecuencia, es más probable que la conducción se produzca a través del HOMO que por orbitales más profundos.
Ahora,\(\sigma\) los enlaces poseen densidades de electrones localizadas entre átomos. Pero\(\pi\) los enlaces compuestos por combinaciones lineales de p orbitales pueden deslocalizarse a lo largo de una cadena o lámina de átomos. Así, si el HOMO es un\(\pi\) enlace, es mucho más fácil empujar un electrón a través de él; veremos algunos ejemplos de esto en la siguiente sección.
Alineación plana con tres vecinos (\(sp^{2}\)hibridación)
Considera un átomo central con tres vecinos equiespaciados en los puntos de un triángulo; como se muestra en la Figura\(\PageIndex{5}\). Arbitrariamente alineamos los átomos en el plano x-y.
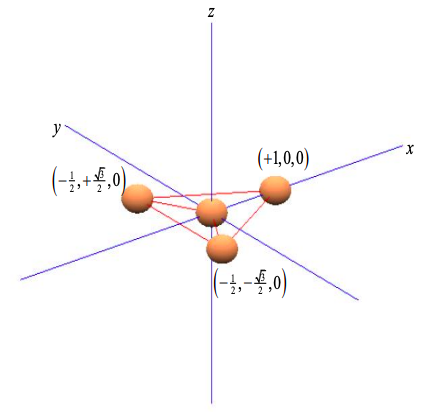
Una vez más, deseamos determinar la contribución de los orbitales del átomo central a los\(\sigma\) enlaces. Si el conjunto de bases consiste en orbitales s y p, solo los orbitales s\(p_{x}\) y\(p_{y}\) atómicos pueden contribuir a los\(\sigma\) enlaces en el plano x-y. \(p_{z}\)los orbitales sólo pueden contribuir a\(\pi\) los vínculos.
Definamos los orbitales atómicos adaptados a simetría que contribuyen individualmente a\(\sigma\) los enlaces generalmente como:
\[ \phi_{\sigma} = c_{s}\phi_{s} + c_{p_{x}}\phi_{p_{x}} + c_{p_{y}}\phi_{p_{y}} \label{8.5.8} \]
El orbital s contribuye igualmente a los tres orbitales atómicos adaptados a simetría. i.e.
\[ |c_{s}|^{2} = \frac{1}{3},\ \ \ c_{s} = \frac{1}{\sqrt{3}} \label{8.5.9} \]
Dado que el\(p_{x}\) orbital está alineado con el eje x, y\(p_{y}\) con el eje y, podemos ponderar los componentes orbitales p por las coordenadas del triángulo de átomos vecinos
\ [\ phi_ {\ sigma} ^ {1} = c_ {s}\ phi_ {s} + c_ {p}\ izquierda (+1\ phi_ {p_ {x}} + 0\ phi_ {p_ {y}}\ derecha)\
\ phi_ {\ sigma} ^ {2} = c_ {s}\ phi_ {s} + c_ {p}\ izquierda (-\ frac {1} {2}\ phi_ {p_ {x}} +\ frac {\ sqrt {3}} {2}\ phi_ {p_ {y}}\ derecha)\
\ phi_ {\ sigma} ^ {3} = c_ {s}\ phi_ {s} + c_ {p}\ izquierda (-\ frac {1} {2}\ phi_ _ {p_ {x}} -\ frac {\ sqrt {3}} {2}\ phi_ {p_ {y}}\ derecha)\ etiqueta {8.5.10}\]
La normalización de cada orbital da
\[ |c_{p}|^{2} = \frac{2}{3},\ \ \ c_{p} = \sqrt{\frac{2}{3}} \label{8.5.11} \]
Por lo tanto,
\ [\ phi_ {\ sigma} ^ {1} =\ frac {1} {\ sqrt {3}}\ phi_ {s} +\ sqrt {\ frac {2} {3}}\ phi_ {p_ {x}} + 0\ phi_ {p_ {y}}\
\ phi_ {\ sigma} ^ {2} =\ frac {1} {\ sq{ 3}}\ phi_ {s} -\ frac {1} {\ sqrt {6}}\ phi_ {p_ {x}} +\ frac {1} {\ sqrt {2}}\ phi_ {p_ {y}}\
\ phi_ {\ sigma} ^ {2} =\ frac {1} {\ sqrt {3}}\ phi_ {s} -\ frac {1} {\ sqrt {6}}\ phi_ {p_ {x}} -\ frac {1} {\ sqrt {2}}\ phi_ {p_ {y}}\ nonumber\]
Esto se conoce como\(sp^{2}\) hibridación ya que hemos combinado uno s orbital atómico, y dos orbitales p atómicos para crear tres orbitales atómicos que contribuyen individualmente a los\(\sigma\) enlaces. El ángulo de unión es de 120º.
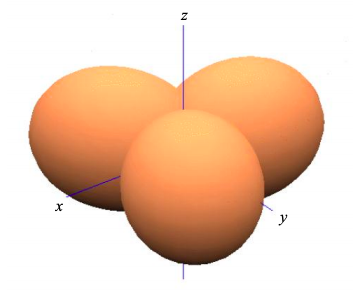
Los orbitales\(p_{z}\) atómicos restantes contribuirán a los orbitales moleculares fronterizos de un material\(sp^{2}\) hibridado; ver por ejemplo eteno en la Figura\(\PageIndex{7}\).
Como en el caso hibridado sp, los electrones en estos orbitales\(\pi\) moleculares pueden ser deslocalizados. Si los electrones se deslocalizan sobre varios átomos vecinos, entonces se dice que la molécula está conjugada. Otro material\(sp^{2}\) hibridado se mostró en la Figura 6.3.1. Se trata de 1,3- butadieno, una cadena de átomos de carbono\(4 \times sp^{2}\) hibridados. Tenga en cuenta la extensa deslocalización de electrones en los\(\pi\) enlaces.
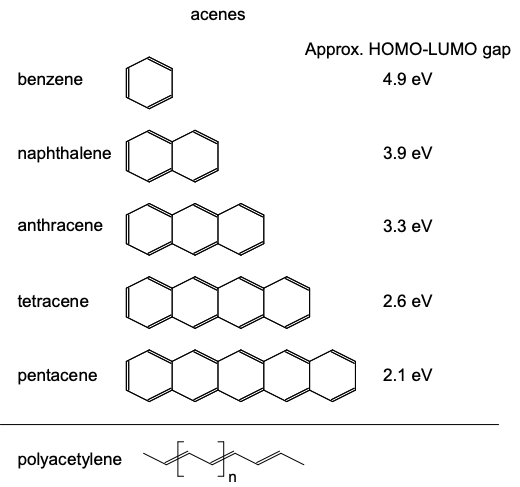
Algunas moléculas arquetípicas conjugadas a base de carbono se muestran en la Figura\(\PageIndex{8}\). En cada material se\(sp^{2}\) hibridan los átomos de carbono (rodeados por tres vecinos en puntos de un triángulo equilátero). Nótese que otra característica típica de los materiales\(sp^{2}\) hibridados es la alternancia de enlaces simples y dobles.
Alineación tetraédrica con cuatro vecinos (\(sp^{3}\)hibridación)
Considera un átomo central con cuatro vecinos equiespaciados. La repulsión entre estos átomos los empujará a las puntas de un tetraedro; ver Figura\(\PageIndex{9}\).
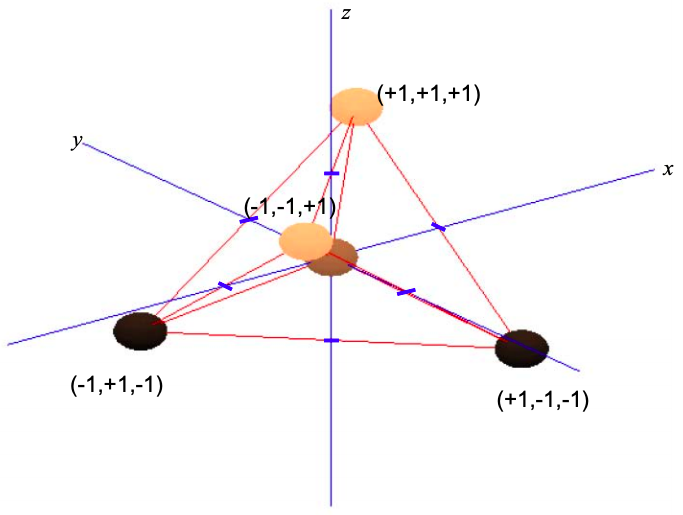
Ahora, todos los orbitales atómicos contribuirán a\(\sigma\) los vínculos. No hay\(\pi\) bonos.
Definamos los orbitales atómicos adaptados a simetría que contribuyen individualmente a\(\sigma\) los enlaces generalmente como:
\[ \phi_{\sigma} = c_{s}\phi_{s} + c_{p_{x}}\phi_{p_{x}} + c_{p_{y}}\phi_{p_{y}} + c_{p_{z}}\phi_{p_{z}} \label{8.5.13} \]
Una vez más, el orbital s contribuye por igual a los cuatro orbitales atómicos adaptados a simetría. i.e.
\[ |c_{s}|^{2} = \frac{1}{4},\ \ \ c_{s} = \frac{1}{2} \label{8.5.14} \]
Dado que el\(p_{x}\) orbital está alineado con el eje x,\(p_{y}\) con el eje y y\(p_{z}\) con el eje z, podemos ponderar los componentes orbitales p por las coordenadas del triángulo de átomos vecinos
\ [\ phi_ {\ sigma} ^ {1} = c_ {s}\ phi_ {s} + (+1\ phi_ {p_ {x}}\ +1\ phi_ {p_ {y}}\ +1\ phi_ {p_ {p_ {x}})
\\ phi_ {\ sigma} ^ {2} = c_ {s}\ phi_ {s} + (-1\ phi_ {p_ {x}}\ +1\ phi_ {p_ {y}}\ -1\ phi_ {p_ {x}})\\
\ phi_ {\ sigma} ^ {3} = c_ {s}\ phi_ {s} + (+1\ phi_ {p_ {p_ {x}}\ -1\ phi_ {p_ {y}}\ -1\ phi_ {p_ {x})\\
\ phi_ {\ sigma} ^ {1} = c_ {s}\ phi_ {s} + (-1\ phi_ {p_ {x}}\ -1\ phi_ {p_ {y}}\ -1\ phi_ {p_ {p_ {x}})\ etiqueta {8.5.15}\]
La normalización de cada orbital da
\[ |c_{p}|^{2} = \frac{1}{4},\ \ \ c_{p} = \frac{1}{2} \label{8.5.16} \]
Por lo tanto,
\ [\ phi_ {\ sigma} ^ {1} =\ frac {1} {2} (\ phi_ {s} +\ phi_ {p_ {x}} +\ phi_ {p_ {y}} +\ phi_ {p_ {z}})\\ phi_ {
\ sigma} ^ {2} =\ frac {1} {2} (\ phi_ {s} -\ phi_ {p_ {x}} +\ phi_ {p_ {y}} -\ phi_ {p_ {p_ {z}})\\ phi_ {
\ sigma} ^ {3} =\ frac {1} {2} (\ phi_ {s} +\ phi_ {p_ {x}} -\ phi_ {p_ {p_ {y}} -\ phi_ {p_ {p_ z}})\\
\ phi_ {\ sigma} ^ {4} =\ frac {1} {2} (\ phi_ {s} -\ phi_ {p_ {x}} -\ phi_ {p_ {p_ {y}} -\ phi_ {p_ {z}})\ label {8.5.17}\]
Esto se conoce como\(sp^{3}\) hibridación ya que hemos combinado uno s orbital atómico, y tres orbitales p atómicos para crear cuatro posibles orbitales atómicos que contribuyen individualmente a los\(\sigma\) enlaces. El ángulo de unión es de 109.5º.
