2.4: Funciones útiles adicionales y transformaciones de Laplace: paso, seno, coseno e integral definida

Describiremos y transformaremos varias funciones matemáticas útiles diferentes. Una característica común de la mayoría de estas funciones es que se definen para tener valores distintos de cero solo para el tiempo positivo, es decir, son cero antes de\(t\) = 0. La función fundamental de este tipo es la función básica de Heaviside unidad-paso (después del ingeniero eléctrico inglés, físico y matemático aplicado Oliver Heaviside, 1850-1925) que se muestra en la Figura\(\PageIndex{1}\):

\ [H (t) =\ left\ {\ begin {array} {ll}
0 &\ text {for} t<0\\
1 &\ text {for} t>0
\ end {array}\ right. \ label {eqn:2.26}\]

\(H(t)\)es adimensional, y está indefinido matemáticamente en la discontinuidad en\(t = 0\). Si queremos escribir una ecuación para una cantidad física de entrada que se aplique rápidamente y permanezca constante a partir de entonces, podemos usarla\(H(t)\) para representarla aproximadamente; por ejemplo, una fuerza de “paso” se\(f_x(t)\) puede describir con la ecuación

\[f_{x}(t)=F \times H(t) \equiv F H(t)\nonumber \]

donde\(F\) está la magnitud de la fuerza dimensional. Para muchas cantidades físicas de entrada, una función de paso es una aproximación idealizada; tal cantidad aumenta rápida pero continuamente, no como un paso puro discontinuo, de cero a un valor constante. [La notación\(H(t)\) utilizada aquí para la función unidad-paso es común pero no estándar; de hecho, no existe un símbolo estándar en la literatura de ingeniería.]

Figura\(\PageIndex{1}\)

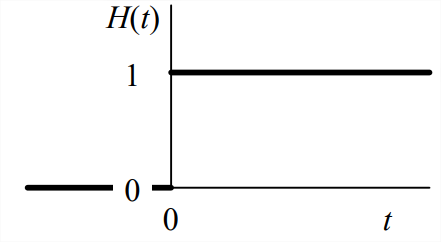
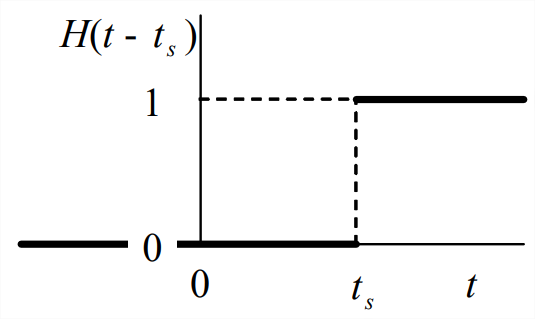
Una función de paso de unidad más general describe un paso que ocurre en algún momento diferente al instante definido como\(t\) = 0. Esta función mostrada en la Figura\(\PageIndex{2}\) es:

\ [H\ left (t-t_ {s}\ right) =\ left\ {\ begin {array} {ll}
0 &\ text {for} t<t_ {s}\\
1 &\ text {for} t>t_ {s}
\ end {array}\ right. \ label {eqn:2.27}\]

Si el tiempo de discontinuidad es\(t_s = 0\), entonces esta función más general se convierte en la función básica de la Ecuación\(\ref{eqn:2.26}\). La transformación de Laplace de\(H\left(t-t_{s}\right)\) es

\[L\left[H\left(t-t_{s}\right)\right]=\int_{t=0}^{t=\infty} e^{-s t} H\left(t-t_{s}\right) d t=\int_{t=t_{s}}^{t=\infty} e^{-s t} d t=\frac{1}{-s} \int_{t-t_{s}}^{t=\infty} d\left(e^{-s t}\right)=-\frac{1}{s}\left(e^{-s \times \infty}-e^{-s t_{s}}\right) \nonumber \]

\[L\left[H\left(t-t_{s}\right)\right]=\frac{e^{-s t_{s}}}{s}\label{eqn:2.28} \]

Obsérvese, en particular, la versión de Ecuación\(\ref{eqn:2.28}\) para la función básica unidad-paso con\(t_s\) = 0:

\[L[H(t)]=\frac{1}{s}\label{eqn:2.29} \]

Frecuentemente usaremos funciones sinusoidales y cosenales del tiempo con frecuencia circular\(\omega\), siendo las funciones distintas de cero solo para el tiempo positivo,\(t\)\(\geq\) 0. Usando notación precisa, tal función sinusoidal, por ejemplo, debería denotarse\(H(t) \times \sin \omega t\); sin embargo, con pocas excepciones, consideraremos mayormente\(t\)\(\geq\) 0, por lo que casi siempre podemos omitir la parte “\(H(t) \times\)” de la ecuación, con el entendimiento implícito de que el análisis aplica solo para \(t\)\(\geq\)0.

Figura\(\PageIndex{2}\)

A continuación derivamos la transformación de Laplace de la función sinusoidal expresando el seno en términos de funciones exponenciales complejas (tarea Problema 2.1) y usando la transformación directa básica de la Ecuación\(\ref{eqn:2.26}\):

\[L[\sin \omega t]=L\left[\frac{e^{j \omega t}-e^{-j \omega t}}{2 j}\right]=\frac{1}{2 j}\left(\frac{1}{s-j \omega}-\frac{1}{s+j \omega}\right)=\frac{1}{2 j}\left(\frac{s+j \omega-(s-j \omega)}{(s-j \omega)(s+j \omega)}\right) \nonumber \]

\[L[\sin \omega t]=\frac{1}{2 j}\left(\frac{2 j \omega}{s^{2}+\omega^{2}}\right)=\frac{\omega}{s^{2}+\omega^{2}}\label{eqn:2.30} \]

Usando un proceso similar, puede derivar (tarea Problema 2.10) la siguiente transformación de Laplace de la función coseno:

\[L[\cos \omega t]=\frac{s}{s^{2}+\omega^{2}}\label{eqn:2.31} \]

Otra transformación útil de Laplace es la de una integral definida. Supongamos que una función físicamente realista\(f(t)\) tiene transformación de Laplace\(F(s)=L[f(t)]\), y que necesitamos la transformación de la integral definida\(\int_{\tau=-\infty}^{\tau=t \geq 0} f(\tau) d \tau\). Tenga en cuenta el límite inferior de\(\tau=-\infty\); generalmente consideraremos\(f(t)\) solo para\(t\)\(\geq\) 0, pero ocasionalmente también se necesita la integral de\(f(t)\) tiempo anterior,\(t\) < 0. La transformación general, que se deriva en el Apéndice A, Sección A-3, es:

\[L\left[\int_{\tau=-\infty}^{\tau=t \geq 0} f(\tau) d \tau\right]=\frac{1}{s} F(s)+\frac{1}{s} \int_{\tau=-\infty}^{\tau=0} f(\tau) d \tau\label{eqn:2.32} \]

Para la mayoría de las aplicaciones, tendremos\(f(t)\) = 0 para\(t\) < 0, para lo cual la transformación más simple es:

\[L\left[\int_{\tau=0}^{\tau=t \geq 0} f(\tau) d \tau\right]=\frac{1}{s} F(s)\label{eqn:2.33} \]

Si consideramos la integral de\(f(t)\) como la primera derivada “negativa” (antiderivada), entonces vemos que la ecuación de transformación\(\ref{eqn:2.32}\) es lógicamente consistente con la ecuación de transformación 2.2.9 para una derivada “positiva”, con respecto tanto a la potencia de\(s\) como al término del valor inicial.