4.1: La transformación de componentes simétricos

La base de esta técnica analítica es una transformación de los tres voltajes y tres corrientes en un segundo conjunto de voltajes y corrientes. Este segundo conjunto se conoce como los componentes simétricos.

Trabajando en amplitudes complejas:

\[\ v_{a}=\operatorname{Re}\left(\underline{V}_{a} e^{j \omega t}\right)\label{1} \]

\[\ v_{b}=\operatorname{Re}\left(\underline{V}_{b} e^{j\left(\omega t-\frac{2 \pi}{3}\right)}\right)\label{2} \]

\[\ v_{c}=\operatorname{Re}\left(\underline{V}_{c} e^{j\left(\omega t+\frac{2 \pi}{3}\right)}\right)\label{3} \]

La transformación se define como:

\ [\\ left [\ begin {array} {l}
\ subrayado {V} _ {1}\
\ subrayado {V} _ {2}\
\ subrayado {V} _ {0}
\ end {array}\ derecha] =\ frac {1} {3}\ left [\ begin {array} {lll}
1 &\ subrayado {a} &\ subrayado {a} {2}\\
1 &\ subrayan {a} ^ {2} &\ subrayado {a}\\
1 & 1 & 1
\ end {array}\ derecha]\ izquierda [\ begin {array} {l}\ label {4}
\ subrayado {V} _ _ {a}\
\ subrayado {V} _ _ {b}\
\ subrayado {V} _ _ {c}
\ end {array}\ derecha]\ nonumber\]

donde el número complejo\(\ \underline{a}\) es:

\[\ \underline{a} \quad=e^{j \frac{2 \pi}{3}} \quad=-\frac{1}{2}+j \frac{\sqrt{3}}{2}\label{5} \]

\[\ \underline{a}^{2}=e^{j \frac{4 \pi}{3}}=e^{-j \frac{2 \pi}{3}}=-\frac{1}{2}-j \frac{\sqrt{3}}{2}\label{6} \]

\[\ \underline{a}^{3} \quad=1\label{7} \]

Esta transformación puede ser utilizada tanto para voltaje como para corriente, y funciona para variables en forma ordinaria así como variables que han sido normalizadas y están en forma por unidad. La inversa de esta transformación es:

\ [\\ izquierda [\ begin {array} {l}
\ subrayado {V} _ _ {a}
\\ subrayado {V} _ _ {b}
\\ subrayado {V} _ _ {c}
\ end {array}\ derecha] =\ left [\ begin {array} {lll}
1 & 1\
\ subrayado {a} ^ {2} &\ subrayado {a} & 1\\
\ subrayado {a} &\ subrayado {a} ^ {2} & 1
\ end {array}\ derecha]\ izquierda [\ begin {array} {l}
\ subrayado {V} _ {1}\
\ subrayado {V} _ {2}\
\ subrayado {V} _ {0}
\ end {array}\ derecha]\ label {8}\]

Las tres variables componentes\(\ \underline{V}_{1}\),\(\ \underline{V}_{2}\),\(\ \underline{V}_{0}\) se denominan, respectivamente, secuencia positiva, secuencia negativa y secuencia cero. Se les llama componentes simétricos porque, tomados por separado, se transforman en conjuntos simétricos de voltajes. Las propiedades de estos componentes se pueden demostrar transformando cada uno de nuevo en variables de fase.

Considere primero el componente de secuencia positiva tomado por sí mismo:

\[\ \underline{V}_{1}=V\label{9} \]

\[\ \underline{V}_{2}=0\label{10} \]

\[\ \underline{V}_{0}=0\label{11} \]

rendimientos:

\[\ \underline{V}_{a}=V \quad \text { or } \quad v_{a}=V \cos \omega t\label{12} \]

\[\ \underline{V}_{b}=\underline{a}^{2} V \quad \text { or } \quad v_{b}=V \cos \left(\omega t-\frac{2 \pi}{3}\right)\label{13} \]

\[\ \underline{V}_{c}=\underline{a} V \quad \text { or } \quad v_{c}=V \cos \left(\omega t+\frac{2 \pi}{3}\right)\label{14} \]

Este es el familiar conjunto equilibrado de voltajes: Fase b retardos fase a por 120 ^o fase c retardos fase b y fase a retardos fase c.

La misma transformación llevada a cabo en una tensión de secuencia negativa:

\[\ \underline{V}_{1}=0\label{15} \]

\[\ \underline{V}_{2}=V\label{16} \]

\[\ \underline{V}_{0}=0\label{17} \]

rendimientos:

\[\ \underline{V}_{a}=V \quad \text { or } \quad v_{a}=V \cos \omega t\label{18} \]

\[\ \underline{V}_{b}=\underline{a} V \quad \text { or } \quad v_{b}=V \cos \left(\omega t+\frac{2 \pi}{3}\right)\label{19} \]

\[\ \underline{V}_{c}=\underline{a}^{2} V \quad \text { or } \quad v_{c}=V \cos \left(\omega t-\frac{2 \pi}{3}\right)\label{20} \]

Esto se llama secuencia negativa porque la secuencia de voltajes se invierte: la fase b ahora lleva la fase a en lugar de retrasarse. Tenga en cuenta que el conjunto de secuencias negativas aún está equilibrado en el sentido de que los componentes de fase aún tienen la misma magnitud y están separados por 120 ^o. La única diferencia entre secuencia positiva y negativa es la rotación de fase. Esto se muestra en la Figura 1.

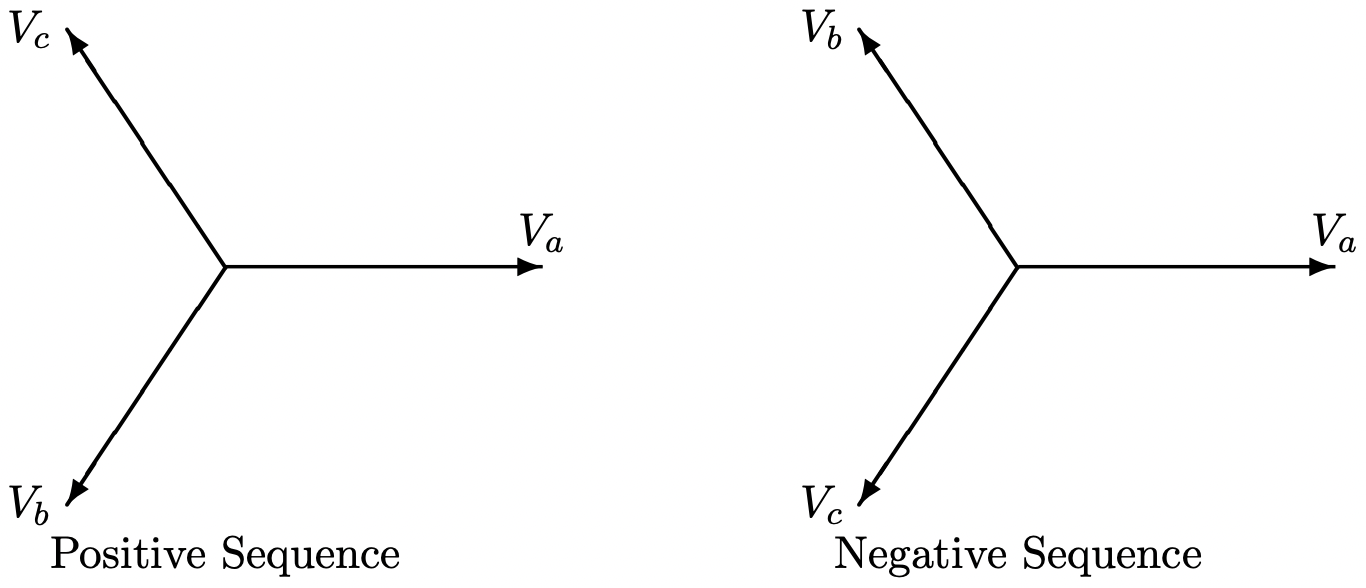Figura 1: Diagrama de fasores: voltajes trifásicos

El tercer componente simétrico es la secuencia cero. Si:

\[\ \underline{V}_{1}=0\label{21} \]

\[\ \underline{V}_{2}=0\label{22} \]

\[\ \underline{V}_{0}=V\label{23} \]

Entonces:

\[\ \underline{V}_{a}=V \quad \text { or } \quad v_{a}=V \cos \omega t\label{24} \]

\[\ \underline{V}_{b}=V \quad \text { or } \quad v_{b}=V \cos \omega t\label{25} \]

\[\ \underline{V}_{c}=V \quad \text { or } \quad v_{c}=V \cos \omega t\label{26} \]

Es decir, las tres fases están variando juntas.

Los conjuntos de secuencias positivas y negativas contienen aquellas partes de la excitación trifásica que representan la secuencia de fase normal e inversa balanceada. Se requiere una secuencia cero para componer la diferencia entre las variables de fase totales y los dos componentes giratorios.

La gran utilidad de los componentes simétricos es que, para la mayoría de los tipos de elementos de red, los componentes simétricos son independientes entre sí. En particular, las impedancias balanceadas y las máquinas giratorias extraerán solo corrientes de secuencia positiva en respuesta a voltajes de secuencia positiva. Por lo tanto, es posible describir una red en términos de subredes, una para cada uno de los componentes simétricos. A estas se les llama redes de secuencia. Una red completamente equilibrada tendrá tres redes de secuencia completamente separadas. Si una red está desequilibrada en un punto determinado, las redes de secuencia se interconectarán en ese punto. La clave para el uso de componentes simétricos en el manejo de situaciones desequilibradas está en aprender a formular esas interconexiones.