12.2: Clasificación de orden cero

Al determinar la calificación de una máquina, podemos considerar dos conjuntos separados de parámetros. El primer conjunto, los parámetros de clasificación elementales, consisten en las inductancias de la máquina, el enlace de flujo interno y la resistencia del estator. A partir de estas y algunas suposiciones sobre la velocidad base y máxima es posible obtener una primera estimación de la calificación y rendimiento del motor. Las estimaciones de desempeño más detalladas, incluida la eficiencia en la operación sostenida, requieren la estimación de otros parámetros. Prestaremos más atención a ese primer conjunto de parámetros, pero intentaremos mostrar cómo se pueden estimar al menos algunos de los parámetros operativos más completos.

Voltaje y Corriente: Rotor Redondo

Para comenzar, considere el circuito equivalente que se muestra en la Figura 5. Este es en realidad el circuito equivalente que describe todas las máquinas sincrónicas de rotor redondo. Es directamente equivalente sólo a algunas de las máquinas que estamos tratando aquí, pero servirá para ilustrar uno o dos puntos importantes.

Lo que se muestra aquí es el circuito equivalente de una sola fase de la máquina. La mayoría de los motores son trifásicos, pero no es difícil realizar la mayor parte del análisis para un número arbitrario de fases. El circuito muestra una tensión interna\(\ E_{a}\) y una reactancia\(\ X\) que junto con la corriente del terminal\(\ I\) determinan la tensión del terminal\(\ V\). En esta imagen se ignora la resistencia de la armadura. Si la máquina está funcionando en el estado estacionario sinusoidal, las cantidades principales son de la forma:

\ (\\ comenzar {alineado}
E_ {a} &=\ omega\ lambda_ {a}\ cos (\ omega t+\ delta)\\
V_ {t} &=V\ cos\ omega t\\
I_ {a} &=I\ cos (\ omega t-\ psi)
\ end {alineado}\)

La máquina está en funcionamiento síncrono si los voltajes internos y externos están al mismo

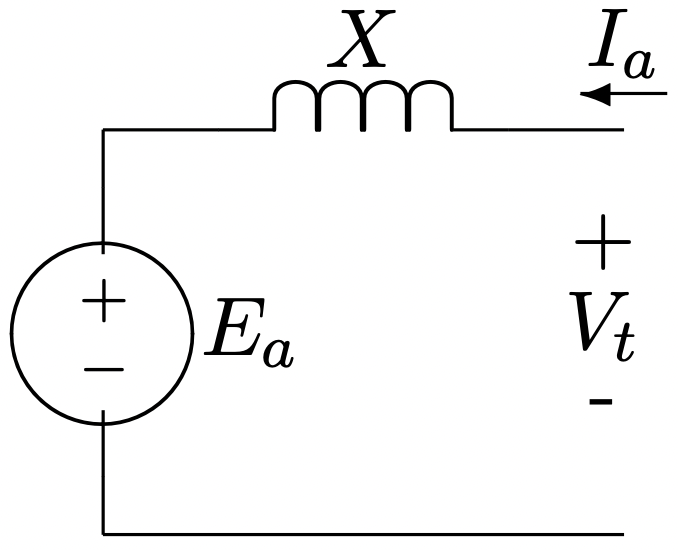Figura 5: Circuito equivalente a máquina síncrona

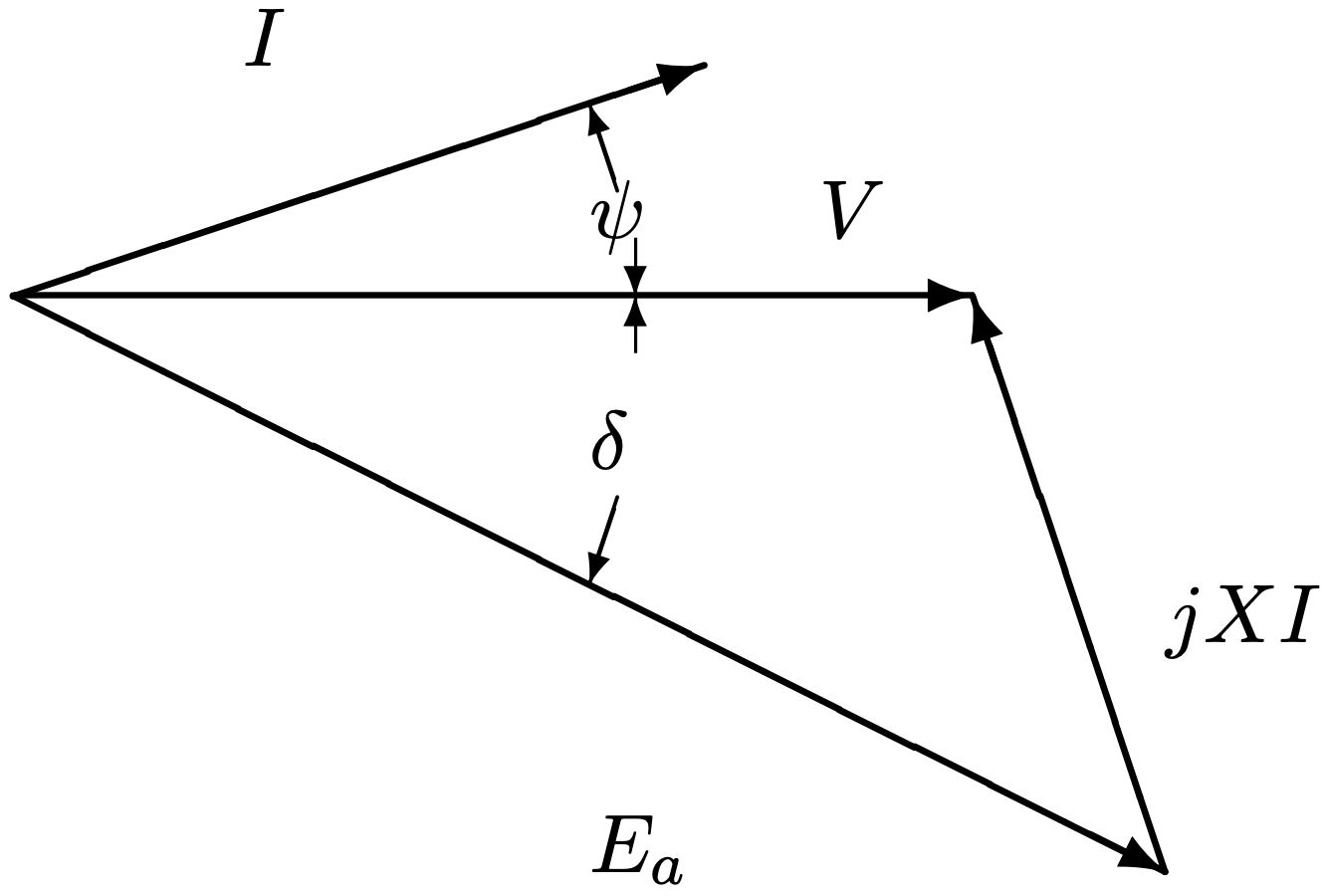Figura 6: Diagrama de fasores para una máquina síncrona

frecuencia y tener una relación de fase constante (o que cambia lentamente)\(\ (\delta)\). La relación entre las variables principales puede ser visualizada por el diagrama fasor que se muestra en la Figura 3.1. El voltaje interno es solo la derivada en el tiempo del flujo interno de los imanes permanentes, y la caída de voltaje en la reactancia de la máquina es también la derivada del tiempo del flujo producido por la corriente del inducido en el entrehierro y en las inductancias de “fuga” de la máquina. Por convención, el ángulo\(\ \psi\) es positivo cuando la corriente se\(\ I\) queda atrás voltaje\(\ V\) y el ángulo\(\ \delta\) es positivo entonces voltaje interno\(\ E_{a}\) conduce voltaje terminal\(\ V\). Por lo que ambos ángulos tienen signo negativo en la situación que se muestra en la Figura 3.1.

Si hay\(\ q\) fases, el tiempo promedio de potencia producida por esta máquina es simplemente:

\(\ P=\frac{q}{2} V I \cos \psi\)

Para la mayoría de las máquinas polifásicas que operan en lo que se denomina operación “balanceada” (todas las fases hacen lo mismo con diferencias de fase uniformes entre fases), el torque (y consecuentemente la potencia) son aproximadamente constantes. Dado que hemos ignorado la potencia disipada en la armadura de la máquina, debe ser cierto que la potencia absorbida por la fuente de voltaje interna es la misma que la potencia del terminal, o:

\(\ P=\frac{q}{2} E_{a} I \cos (\psi-\delta)\)

Dado que en el estado estacionario:

\(\ P=\frac{\omega}{p} T\)

donde\(\ T\) es el par y\(\ \omega / p\) es la velocidad de rotación mecánica, el par se puede derivar de las cantidades terminales simplemente:

\(\ T=p \frac{q}{2} \lambda_{a} I \cos (\psi-\delta)\)

En principio, entonces, para determinar el par y por lo tanto la potencia nominal de una máquina solo es necesario determinar el flujo interno, la capacidad de corriente terminal y la capacidad de velocidad del rotor. De hecho es casi así de simple. Desafortunadamente, el modelo que se muestra en la Figura 5 no está del todo completo para algunos de los motores con los que vamos a tratar, y debemos ir un nivel más a la teoría de la máquina.

Una pequeña teoría de dos reacciones

El material de esta subsección se enmarca en términos de teoría trifásica de\(\ (q=3)\) máquinas, pero en realidad es generalizable a un número arbitrario de fases. Supongamos que tenemos una máquina cuya armadura trifásica puede caracterizarse por flujos internos e inductancia que, en general, pueden no ser constantes sino que es función de la posición del rotor. Tenga en cuenta que el modelo simple que presentamos en la subsección anterior no se ajusta a esta imagen, ya que asume una inductancia terminal constante. En ese caso, tenemos:

\[\ \underline{\lambda}_{p h}=\underline{\underline{L}}_{p h} \underline{\underline{I}}_{p h}+\underline{\lambda_{R}}\label{1} \]

donde\(\ \underline{\lambda_{R}}\) está el conjunto de flujos producidos internamente (a partir de los imanes permanentes) y el devanado del estator puede tener inductancias tanto autocomo mutuas.

Ahora, nos parece útil hacer una transformación en estos flujos del estator de la siguiente manera: cada cantidad de armadura, incluyendo flujo, corriente y voltaje, se proyecta en un sistema de coordenadas que se fija al rotor. Esto suele llamarse la Transformación del Parque. Para una máquina trifásica es:

\ [\\ left [\ begin {array} {c}
u_ {d}\\
u_ {q}\\
u_ {0}
\ end {array}\ right] =\ subrayado {u} _ {d q} =\ subrayado {\ subrayado {T} u} _ {p h} =\ subrayado {\ subrayado {T}}\ left [\ begin {array} {l}
u_ {a}\\
u_ {b}\\
u_ {c}
\ end {array}\ derecha]\ label {2}\]

Donde la transformación y su inversa son:

\ [\\ subrayado {\ subrayado {T}} =\ frac {2} {3}\ izquierda [\ begin {array} {ccc}
\ cos\ theta &\ cos\ izquierda (\ theta-\ frac {2\ pi} {3}\ derecha) &\ cos\ izquierda (\ theta+\ frac {2\ pi} {3}\ derecha)\
-\ sin\ theta & -\ sin\ izquierda (\ theta-\ frac {2\ pi} {3}\ derecha) & -\ sin\ izquierda (\ theta+\ frac {2\ pi} {3}\ derecha) \
\ frac {1} {2} &\ frac {1} {2} &\ frac {1} {2}
\ end {array}\ derecha]\ label {3}\]

\ [\\ subrayado {\ subrayado {T}} ^ {-1} =\ izquierda [\ begin {array} {ccc}
\ cos\ theta & -\ sin\ theta & 1\\
\ cos\ izquierda (\ theta-\ frac {2\ pi} {3}\ derecha) & -\ sin\ izquierda (\ theta-\ frac {2\ pi} {3}\ derecha) & 1\\
\ cos\ izquierda (\ theta+\ frac {2\ pi} {3}\ derecha) & -\ sin\ izquierda (\ theta+\ frac {2\ pi} {3}\ derecha) & 1
\ end {array}\ derecha]\ label {4}\]

Es fácil demostrar que las cantidades polifásicas equilibradas en el marco estacionario, o variable de fase, se traducen en cantidades constantes en el llamado cuadro “d-q”. Por ejemplo:

\ (\\ comenzar {alineado}
I_ {a} &=I\ cos\ omega t\\
I_ {b} &=I\ cos\ izquierda (\ omega t-\ frac {2\ pi} {3}\ derecha)\\
I_ {c} &=I\ cos\ izquierda (\ omega t+\ frac {2\ pi} {3}\ derecha)\
\ theta &=\ omega t+\ theta_ {0}
\ final {alineado}\)

mapas para:

\ (\\ comenzar {alineado}
I_ {d} &=I\ cos\ theta_ {0}\\
I_ {q} &=-I\ sin\ theta_ {0}
\ end {alineado}\)

Ahora, si\(\ \theta=\omega t+\theta_{0}\), el sistema de coordenadas de transformación se elige correctamente y el eje “d-” se corresponderá con el eje sobre el que los imanes del rotor están haciendo flujo positivo. Eso sucede si, cuando\(\ \theta=0\), la fase A está vinculando el flujo positivo máximo de los imanes permanentes. Si este es el caso, los flujos internos son:

\ (\\ begin {array} {l}
\ lambda_ {a a} =\ lambda_ {f}\ cos\ theta\
\ lambda_ {a b} =\ lambda_ {f}\ cos\ izquierda (\ theta-\ frac {2\ pi} {3}\ derecha)\
\ lambda_ {a c} =\ lambda_ {f}\ cos\ izquierda (\ theta+\ frac {2\ pi} {3}\ derecha)
\ end {array}\)

Ahora bien, si calculamos los flujos en el marco d-q, tenemos:

\[\ \underline{\lambda}_{d q}=\underline{\underline{L}}_{d q} \underline{I}_{d q}+\underline{\lambda}_{R}=\underline{\underline{T L}}_ {p h} \underline{\underline{T}}^{-1} \underline{I}_{d q}+\underline{\lambda}_{R}\label{5} \]

Ahora: hay que señalar aquí dos cosas. La primera es que, si el sistema de coordenadas ha sido elegido como se ha descrito anteriormente, el flujo inducido por el rotor es, en el marco d-q, simplemente:

\ [\\ subrayado {\ lambda} _ {R} =\ izquierda [\ begin {array} {l}
\ lambda_ {f}\\
0\
0
\ end {array}\ derecha]\ label {6}\]

Es decir, los imanes producen flujo solo en el eje d-.

Lo segundo a tener en cuenta es que, bajo ciertos supuestos, las inductancias en el marco d-q son independientes de la posición del rotor y no tienen términos mutuos. Es decir:

\ [\\ subrayado {\ subrayado {L}} _ {d q} =\ subrayado {\ subrayado {T L}} _ {p h}\ subrayado {\ subrayado {T}} ^ {-1} =\ left [\ begin {array} {lll}
L_ {d} & 0 &
0\\ 0 & L_ {q} &
0\\ 0 & L_ 0}
\ end {array}\ derecha]\ label {7}\]

La aseveración de que las inductancias en el marco d-q son constantes en realidad es cuestionable, pero está lo suficientemente cerca de ser cierta y los análisis que la utilizan han demostrado estar lo suficientemente cerca como para ser correctos que (la aserción) se ha mantenido a la altura de la prueba del tiempo. De hecho, las desviaciones de la independencia en la posición del rotor son pequeñas. La independencia de los ejes (es decir, ausencia de inductancias mutuas en el marco d-q) es correcta porque los dos ejes son físicamente ortogonales. Tendemos a ignorar el tercer eje, o “cero” en este análisis. No se empareja a nada más y no tiene ni flujo ni corriente de todos modos. Tenga en cuenta que las inductancias de los ejes directo y cuadratura son, en principio, fáciles de calcular. Ellos son

dirigir el eje la inductancia de una de las fases de la armadura (corregida por el hecho de múltiples fases) con el rotor alineado con el eje de la fase, y

eje cuadratura la inductancia de una de las fases con el rotor alineado 90 grados eléctricos lejos del eje de esa fase.

A continuación, el voltaje de la armadura es, ignorando la resistencia, dado por:

\[\ \underline{V}_{p h}=\frac{d}{d t} \underline{\lambda}_{p h}=\frac{d}{d t} \underline{\underline{T}}^{-1} \underline{\lambda}_{d q}\label{8} \]

y que la tensión de la armadura transformada debe ser:

\ [\\ comenzar {alineado}
\ subrayado {V} _ {d q} &=\ subrayado {\ subrayado {T} V} _ {p h}\\
&=\ subrayado {\ subrayado {T}}\ frac {d} {d t}\ left (\ subrayado {\ subrayado {\ subrayado {T}} ^ {-1}\ subrayado {\ lambda} _ {d q}\ derecha)\\
&=\ frac {d} {d t}\ subrayado {\ lambda} _ {d q} +\ izquierda (\ subrayado {\ subrayado {T}}\ frac {d} {d t}\ subrayado {\ subrayado {T}} ^ {-1}\ derecha)\ subrayado {\ lambda} _ {d q}
\ final {alineado}\ etiqueta {9}\]

El segundo término en este expresa “voltaje de velocidad”. Una buena cantidad de sencillos pero tediosos rendimientos de manipulación:

\ [\\ subrayado {\ subrayado {T}}\ frac {d} {d t}\ subrayado {\ subrayado {T}} ^ {-1} =\ left [\ begin {array} {ccc}
0 & -\ frac {d\ theta} {d\ theta} {d t} & 0\\ frac {d\ theta} {d t} &
0 & 0 & 0 0
\ end {array}\ derecha]\ label {10}\]

Las expresiones de voltaje de los ejes directo y cuadratura son entonces:

\[\ V_{d}=\frac{d \lambda_{d}}{d t}-\omega \lambda_{q}\label{11} \]

\[\ V_{q}=\frac{d \lambda_{q}}{d t}+\omega \lambda_{d}\label{12} \]

donde

\(\ \omega=\frac{d \theta}{d t}\)

La potencia instantánea viene dada por:

\[\ P=V_{a} I_{a}+V_{b} I_{b}+V_{c} I_{c}\label{13} \]

Usando las transformaciones dadas anteriormente, se puede demostrar que esto es:

\[\ P=\frac{3}{2} V_{d} I_{d}+\frac{3}{2} V_{q} I_{q}+3 V_{0} I_{0}\label{14} \]

que, a su vez, es:

\[\ P=\omega \frac{3}{2}\left(\lambda_{d} I_{q}-\lambda_{q} I_{d}\right)+\frac{3}{2}\left(\frac{d \lambda_{d}}{d t} I_{d}+\frac{d \lambda_{q}}{d t} I_{q}\right)+3 \frac{d \lambda_{0}}{d t} I_{0}\label{15} \]

Entonces, al señalar que\(\ \omega=p \Omega\) y que (15) describe la potencia del terminal eléctrico como la suma de la potencia del eje y la tasa de cambio de la energía almacenada, podemos deducir que el par viene dado por:

\[\ T=\frac{q}{2} p\left(\lambda_{d} I_{q}-\lambda_{q} I_{d}\right)\label{16} \]

Tenga en cuenta que hemos declarado una generalización a una máquina de fase q a pesar de que la derivación aquí dada se realizó para el\(\ q=3\) caso. Por supuesto, las máquinas trifásicas son, con mucho, el caso más común. Las máquinas con mayor número de fases se comportan de la misma manera (y esta generalización es válida para todos los fines a los que la ponemos), pero hay más variables de rotor análogas al “eje cero”.

Ahora bien, señalando que, en general,\(\ L_{d}\) y no\(\ L_{q}\) son necesariamente iguales,

\[\ \lambda_{d}=L_{d} I_{d}+\lambda_{f}\label{17} \]

\[\ \lambda_{q}=L_{q} I_{q}\label{18} \]

entonces el par viene dado por:

\[\ T=p \frac{q}{2}\left(\lambda_{f}+\left(L_{d}-L_{q}\right) I_{d}\right) I_{q}\label{19} \]

Encontrar la capacidad de par

Para accionamientos de alto rendimiento, generalmente asumiremos que la fuente de alimentación, generalmente un inversor, puede suministrar corrientes en la relación espacial correcta al rotor para producir par de alguna manera razonablemente efectiva. Mostraremos en esta sección cómo determinar, dado un par requerido (o si el par está limitado por voltaje o corriente que discutiremos anon), cuáles son los valores de\(\ I_{d}\) y\(\ I_{q}\) deben ser. Entonces la fuente de alimentación, dado algunos medios para determinar dónde está el rotor (el valor instantáneo de\(\ \theta\)), utilizará la transformación inversa de Park para determinar el valor instantáneo requerido para las corrientes de fase. Esta es la esencia de lo que se conoce como “control orientado al campo”, o poner las corrientes del estator en la ubicación correcta en el espacio para producir el par requerido.

Nuestro objetivo en esta sección es, dados los parámetros elementales del motor, encontrar la capacidad del motor para producir torque. Hay tres cosas a considerar aquí:

• La corriente de la armadura es limitada, generalmente por calentamiento,
• Un segundo límite es la capacidad de voltaje de la fuente, particularmente a alta velocidad, y
• Si la máquina está operando dentro de estos dos límites, debemos considerar la colocación óptima de las corrientes (es decir, cómo obtener el mayor par por unidad de corriente para minimizar las pérdidas).

A menudo la discusión de la colocación actual se lleva a cabo utilizando, como herramienta para visualizar lo que está sucediendo, el\(\ I_{q}\) plano\(\ I_{d}\),. La operación en estado estacionario implica un solo punto en este plano. En la Figura 7 se muestra una ilustración sencilla. La capacidad de corriente de armadura limitada térmicamente se representa como un círculo alrededor del origen, ya que la magnitud de la corriente de armadura es solo la longitud de un vector desde el origen en este espacio. Tenga en cuenta que ya que en general, para máquinas de imanes permanentes con

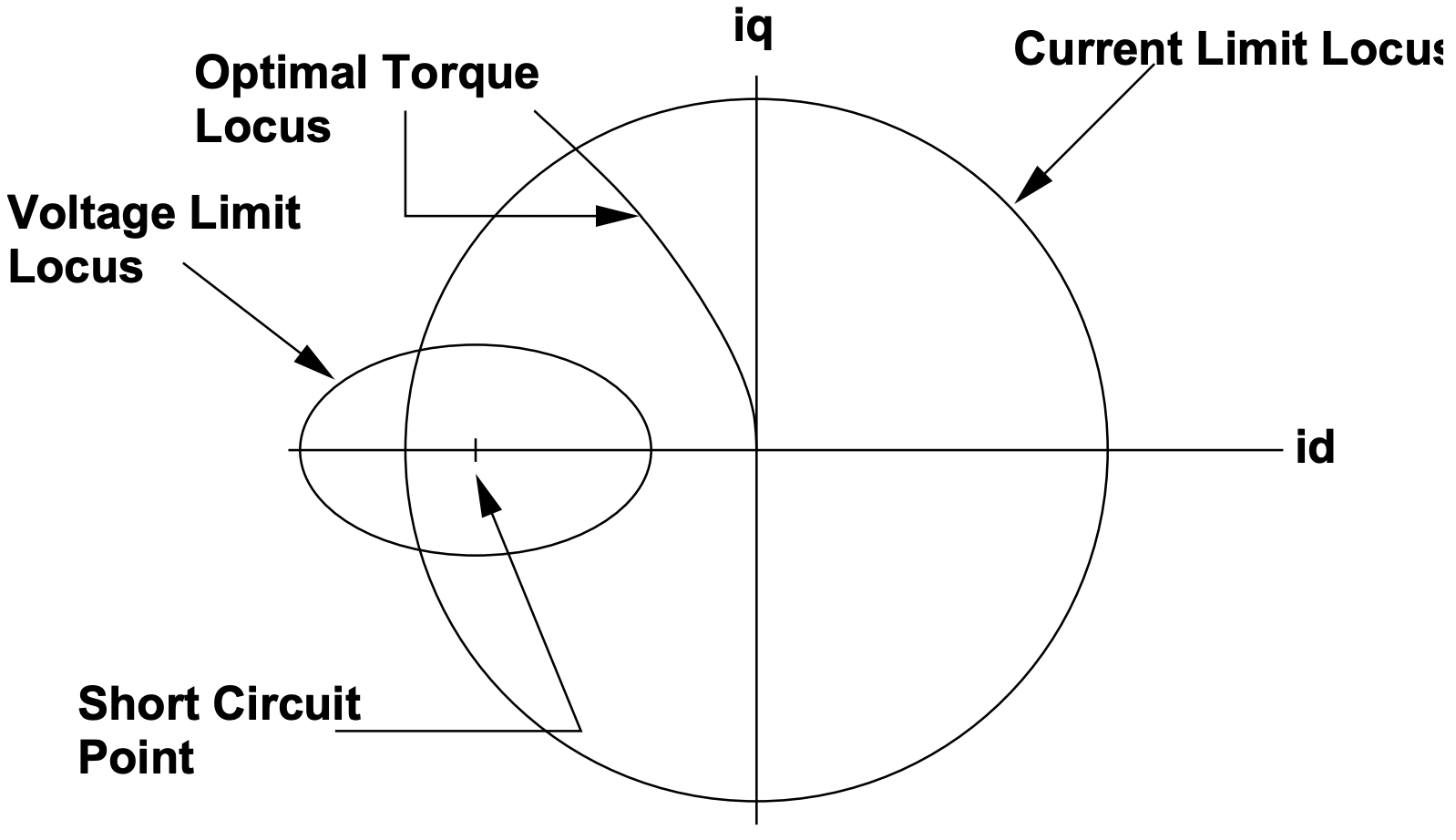Figura 7: Límites a la Operación

imanes enterrados\(\ L_{d}<L_{q}\), por lo que el funcionamiento óptimo de la máquina será con negativo\(\ I_{d}\). Mostraremos cómo determinar esta operación óptima anon, pero en general seguirá una curva en el\(\ I_{q}\) plano\(\ I_{d}\), como se muestra.

Finalmente, una elipse describe el límite de voltaje. Para comenzar, considere qué pasaría si los terminales de la máquina fueran cortocircuitados para que así\(\ V=0\). Si la máquina está funcionando a una velocidad suficientemente alta para que la resistencia de la armadura sea insignificante, la corriente de armadura sería simplemente:

\ (\\ begin {array} {l}
I_ {d} =-\ frac {\ lambda_ {f}} {L_ {d}}\\
I_ {q} =0
\ end {array}\)

Ahora, los loci de flujo constante resultan ser elipses alrededor de este punto en el plano. Dado que el flujo terminal es proporcional al voltaje e inversamente proporcional a la frecuencia, si la máquina está funcionando con un voltaje terminal dado, la capacidad de ese voltaje para mandar corriente en el\(\ I_{q}\) plano\(\ I_{d}\), es una elipse cuyo tamaño “se encoge” a medida que aumenta la velocidad.

Para simplificar las matemáticas involucradas en esta estimación, normalizamos reactancias, flujos, corrientes y pares. Primero, definamos el flujo base para que sea simple\(\ \lambda_{b}=\lambda_{f}\) y la corriente base\(\ I_{b}\) sea la capacidad de la armadura. Luego definimos dos reactancias por unidad:

\[\ x_{d}=\frac{L_{d} I_{b}}{\lambda_{b}}\label{20} \]

\[\ x_{q}=\frac{L_{q} I_{b}}{\lambda_{b}}\label{21} \]

A continuación, defina el par base para que sea:

\(\ T_{b}=p \frac{q}{2} \lambda_{b} I_{b}\)

y luego, dadas las corrientes por unidad\(\ i_{d}\) y\(\ i_{q}\), el par por unidad es simplemente:

\[\ t_{e}=\left(1-\left(x_{q}-x_{d}\right) i_{d}\right) i_{q}\label{22} \]

Es bastante sencillo (pero un poco tedioso) mostrar que el lugar de funcionamiento óptimo de corriente (es decir, el par más grande para una magnitud de corriente dada o la magnitud de corriente más pequeña para un par dado) está a lo largo de la curva:

\[\ i_{d}=-\sqrt{\frac{i_{a}^{2}}{2}+2\left(\frac{1}{4\left(x_{q}-x_{d}\right)}\right)^{2}-\frac{1}{2\left(x_{q}-x_{d}\right)} \sqrt{\left(\frac{1}{4\left(x_{q}-x_{d}\right)}\right)^{2}+\frac{i_{a}^{2}}{2}}}\label{23} \]

\[\ i_{q}=-\sqrt{\frac{i_{a}^{2}}{2}-2\left(\frac{1}{4\left(x_{q}-x_{d}\right)}\right)^{2}+\frac{1}{2\left(x_{q}-x_{d}\right)} \sqrt{\left(\frac{1}{4\left(x_{q}-x_{d}\right)}\right)^{2}+\frac{i_{a}^{2}}{2}}}\label{24} \]

El “punto de clasificación” será el punto a lo largo de esta curva cuando\(\ i_{a}=1\), o donde esta curva cruce el círculo de capacidad de la armadura en el\(\ i_d\)\(\ i_q\) plano. Cabe señalar que este conjunto de expresiones sólo funciona para máquinas sobresalientes. Para máquinas no salientes, por supuesto, la corriente de par óptimo está en el eje q. En general, para máquinas con prominencia, el par “por unidad” no será la unidad en la clasificación, de modo que el par nominal o “Velocidad base” no es el par “Base”, sino:

\[\ T_{r}=T_{b} \times t_{e}\label{25} \]

donde\(\ t_{e}\) se calcula en el punto de calificación (es decir,\(\ i_{a}=1\)\(\ i_{d}\) y y\(\ i_{q}\) según (23) y (24)).

Para velocidades suficientemente bajas, la unidad electrónica de potencia puede ordenar la corriente óptima para producir un par de torsión hasta la nominal. No obstante, para velocidades superiores a la “Velocidad Base”, esto ya no es cierto. Defina un flujo terminal por unidad:

\(\ \psi=\frac{V}{\omega \lambda_{b}}\)

La operación a una magnitud de flujo dada implica:

\(\ \psi^{2}=\left(1+x_{d} i_{d}\right)^{2}+\left(x_{q} i_{q}\right)^{2}\)

que es una elipse en el\(\ i_{q}\) plano\(\ i_{d}\),. La Velocidad Base es aquella velocidad a la que esta elipse cruza el punto donde la curva de corriente óptima cruza la capacidad de la armadura. La operación al par más alto alcanzable (para una velocidad dada) generalmente implica corrientes del eje d que son más altas que las del lugar óptimo de la corriente. Lo que está sucediendo aquí es que la corriente del eje d (negativa) sirve para reducir el flujo efectivo de la máquina y, por lo tanto, el voltaje que limita la corriente del eje q Por lo tanto, el funcionamiento por encima de la velocidad base a menudo se denomina “debilitamiento del flujo”.

La estrategia para elegir la trayectoria correcta para la corriente en el\(\ i_{q}\) plano\(\ i_{d}\), depende del valor de la reactancia por unidad\(\ x_{d}\). Para valores de\(\ x_{d}>1\), es posible producir algún par a cualquier velocidad. Para los valores de\(\ x_{d}<1\), hay una velocidad para la cual ningún punto en la capacidad de corriente del inducido está dentro de la elipse limitadora de voltaje, por lo que el par útil ha ido a cero. Generalmente, el punto de operación de par máximo es la intersección del límite de corriente de la armadura y la elipse limitadora de voltaje:

\[\ i_{d}=\frac{x_{d}}{x_{q}^{2}-x_{d}^{2}}-\sqrt{\left(\frac{x_{d}}{x_{q}^{2}-x_{d}^{2}}\right)^{2}+\frac{x_{q}^{2}-\psi^{2}+1}{x_{q}^{2}-x_{d}^{2}}}\label{26} \]

\[\ i_{q}=\sqrt{1-i_{d}^{2}}\label{27} \]

Tabla 1: Máquina de ejemplo

Inductancia del eje D	2.53 MHy
Inductancia del eje Q	6.38 MhY
Flujo Interno	58,1 MwB
Corriente de la armadura	30 A

Tabla 2: Características de funcionamiento de la máquina de ejemplo

Corriente por unidad del eje D en el punto nominal	\(\ i_{d}\)	-.5924
Corriente por unidad del eje Q en el punto de clasificación	\(\ i_{q}\)	.8056
Reactancia de eje D por unidad	\(\ x_{d}\)	1.306
Reactancia de eje Q por unidad	\(\ x_{q}\)	3.294
Par nominal (Nm)	\(\ T_{r}\)	9.17
Voltaje de terminal en el punto base (V)		97

Puede ser que no haya intersección entre la capacidad de la armadura y la elipse limitadora de voltaje. Si este es el caso y si\(\ x_{d}<1\), la capacidad de par a la velocidad dada es cero.

Si, por otro lado\(\ x_{d}>1\), puede ser que la intersección entre la elipse limitadora de voltaje y el límite de corriente de armadura no sea el punto de par máximo. Para averiguarlo, calculamos el punto de par máximo en la elipse limitadora de voltaje. Esto se hace de la manera habitual diferenciando el par con respecto a\(\ i_{d}\) mientras se mantiene la relación entre\(\ i_{d}\) y\(\ i_{q}\) estar en la elipse. El álgebra es un poco desordenado, y resulta en:

\[\ i_{d}=-\frac{3 x_{d}\left(x_{q}-x_{d}\right)-x_{d}^{2}}{4 x_{d}^{2}\left(x_{q}-x_{d}\right)}-\sqrt{\left(\frac{3 x_{d}\left(x_{q}-x_{d}\right)-x_{d}^{2}}{4 x_{d}^{2}\left(x_{q}-x_{d}\right)}\right)^{2}+\frac{\left(x_{q}-x_{d}\right)\left(\psi^{2}-1\right)+x_{d}}{2\left(x_{q}-x_{d}\right) x_{d}^{2}}}\label{28} \]

\[\ i_{q}=\frac{1}{x_{q}} \sqrt{\psi^{2}-\left(1+x_{d} i_{d}\right)^{2}}\label{29} \]

Ordinariamente, probablemente sea más fácil computar (28) y (29) primero, luego probar para ver si las corrientes están fuera de la capacidad de la armadura, y si lo están, usar (26) y (27).

Estas expresiones nos dan la capacidad de estimar la curva par-velocidad para una máquina. A modo de ejemplo, la máquina descrita por los parámetros citados en el Cuadro 1 es una máquina (nominal) de 3 HP, 4 polos, 3000 RPM.

El punto de operación nominal resulta tener los siguientes atributos:

Los loci de operación en el\(\ I_{q}\) plano\(\ I_{d}\), se muestran en la Figura 8. El límite de corriente de la armadura se muestra sólo en el segundo y tercer cuadrantes, por lo que se muestra como semicírculo. Las dos elipses corresponden con el punto nominal (la elipse más grande) y con una velocidad que es tres veces nominal (9000 RPM). El locus de corriente de par óptimo se puede ver que va desde el origen hasta el punto de clasificación, y el lugar de operación de mayor velocidad sigue el límite de corriente de la armadura. La Figura 9 muestra las curvas de par/velocidad y potencia/velocidad. Tenga en cuenta que este tipo de máquina solo se aproxima a la operación de “potencia constante” a velocidades por encima de la “base” o velocidad del punto nominal.

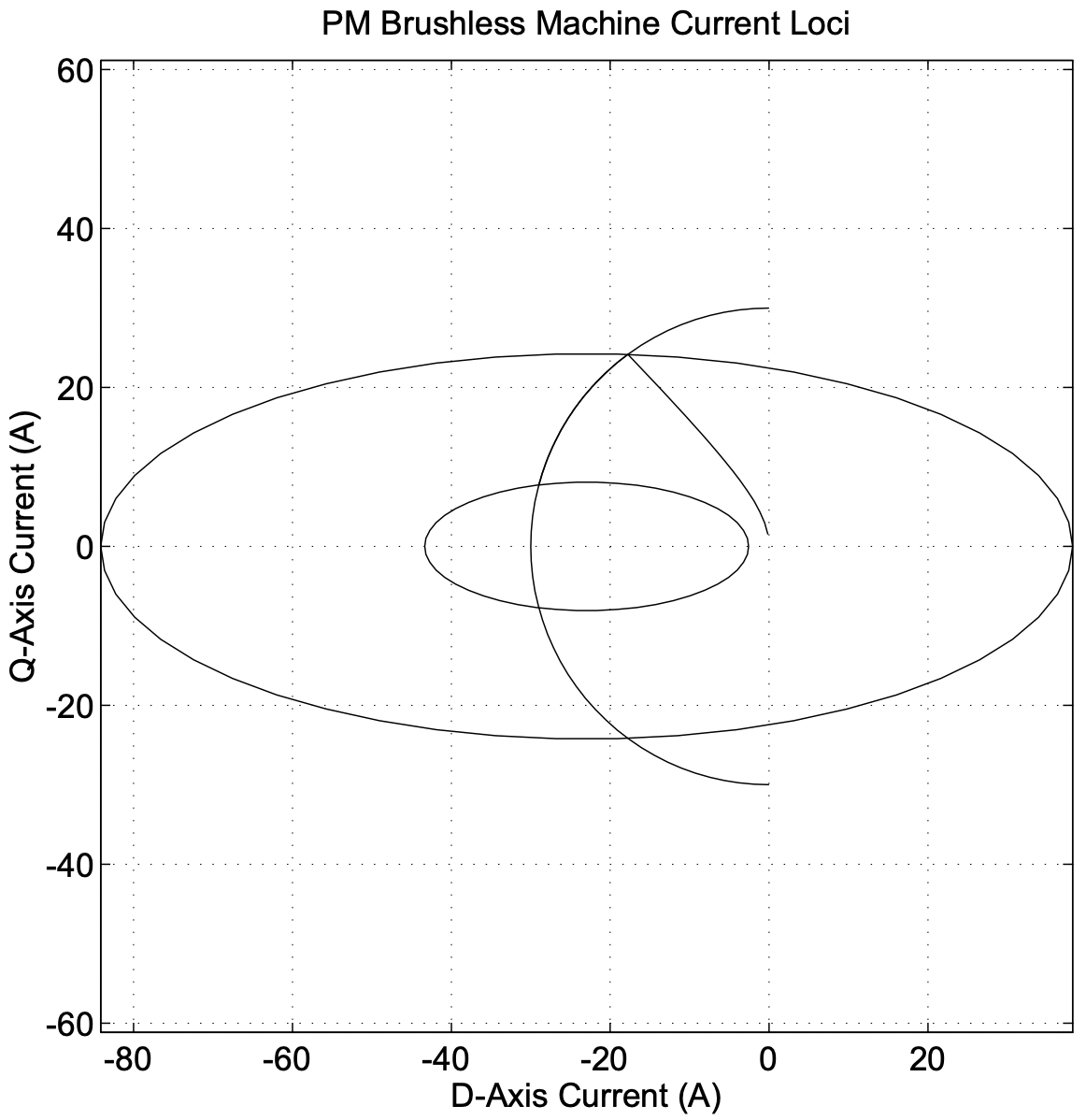Figura 8: Loci de corriente de funcionamiento de la máquina de ejemplo

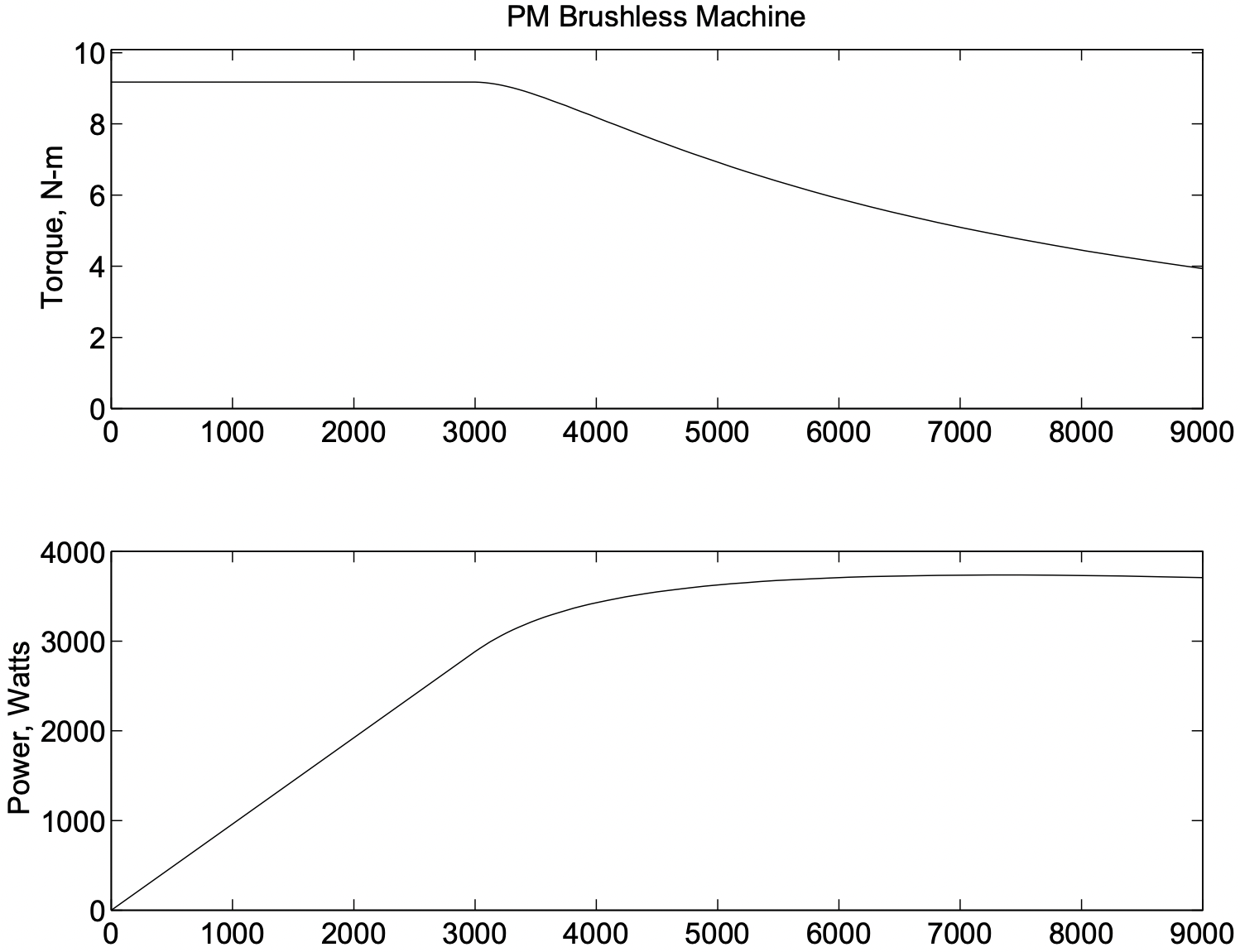Figura 9: Capacidad de par y velocidad de potencia