9.1: El peine de modo

Supongamos que la envolvente del pulso, la frecuencia de repetición y la frecuencia central ya no cambian. Después se esboza la señal correspondiente en el dominio del tiempo en la Figura 9.1.

Figura 9.1: Tren de pulsos emitido desde un láser bloqueado en modo libre de ruido. Los pulsos pueden tener chirrido. La envolvente de intensidad se repite con frecuencia de repetición\(f_R\). El campo eléctrico sólo es periódico con la tasa\(f_{CE}\) si está relacionado con la tasa de repetición por un número racional.

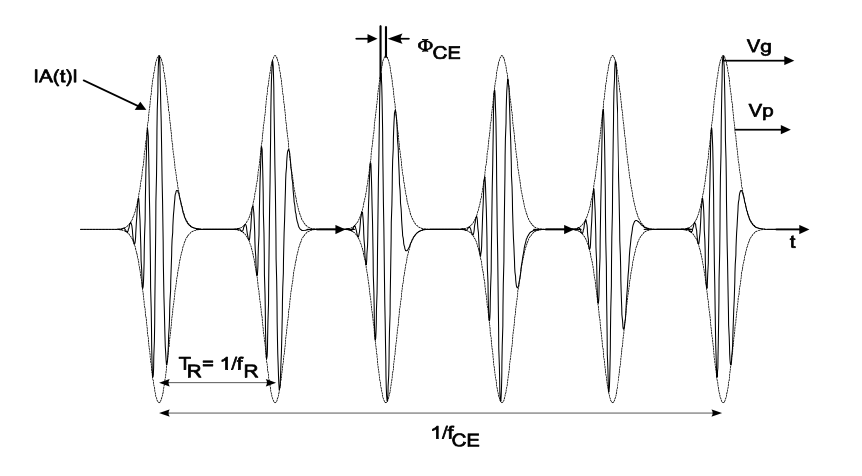
El pulso\(a(T = mT_r, t)\) es la solución de estado estacionario de la ecuación maestra que describe el sistema láser, tal como se estudió en el capítulo 6. Supongamos que la solución de estado estacionario es un solitón purturado según la ecuación (6.3.3).

\[a(t, T) = \left (A_0 \text{sech} (\dfrac{t- t_0}{\tau}) + a_c (T, t) \right ) e^{-j \phi_0 \tfrac{T}{T_R}} \nonumber \]

con el desplazamiento de fase del solitón

\[\phi_0 = \dfrac{1}{2} \delta A_0^2 = \dfrac{|D|}{\tau^2} \nonumber \]

Por lo tanto, hay un desplazamiento de fase de envolvente portadora\(\Delta \phi_{CE}\) de pulso a pulso dado por

\[\begin{array} {rcl} {\Delta \phi_{CE}} & = & {\left (\dfrac{1}{v_g} - \dfrac{1}{v_p} \right )|_{\omega_c} 2L - \phi_0 + \text{mod}(2\pi)} \\ {} & = & {\omega_c T_R \left (1 - \dfrac{v_g}{v_p} \right ) - \phi_0 + \text{mod} (2\pi)} \end{array} \nonumber \]

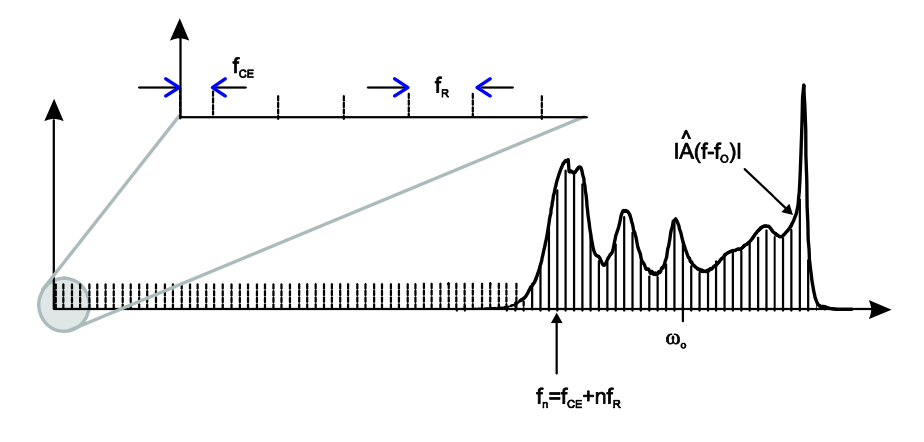
La transformada de Fourier del tren de pulsos imperturbable es

\[\begin{array} {rcl} {\hat{A} (\omega)} & = & {\hat{a} (\omega - \omega_c) \sum_{m = -\infty}^{+\infty} e^{j(\Delta \phi_{CE} - (\omega - \omega_c)T_R)m}} \\ {} & = & {\hat{a} (\omega - \omega_c) \sum_{m = -\infty}^{+\infty} e^{jmT_R (\tfrac{\Delta \phi_{CE}}{T_R} - \omega)}} \\ {} & = & {\hat{a} (\omega - \omega_c) \sum_{m = -\infty}^{+\infty} T_R \delta \left (\omega - \left (\dfrac{\Delta \phi_{CE}}{T_R} + n \omega_R \right ) \right )} \end{array} \nonumber \]

que se muestra en la Figura 9.2. Cada línea de peine es desplazada por la frecuencia de desplazamiento de envolvente portadora\(f_{CE} = \tfrac{\Delta \phi_{CE}}{2\pi T_R}\) desde el origen

Figura 9.2: Peine de modo opitcal de una salida láser de modo bloqueado.

Para obtener ecuaciones autoconsistentes para la frecuencia de repetición, la frecuencia central y los otros parámetros de pulso se emplea la teoría de perturbación de solitón. Esto se justifica para el caso, donde el pulso de estado estacionario está cerca de un solitón, es decir, para el caso del absorbedor saturable rápido, esta es la solución libre de chirp, ocurriendo cuando la relación de filtrado de ganancia a dispersión es igual a la relación de acción SAM a modulación de autofase, ver Ecuación (6.2.43). Entonces la solución de pulso en la\(m\) -ésima ida y vuelta es una solución de la ecuación de Schrödinger no lineal estabilizada por la dinámica irreversible y sujeta a perturbaciones adicionales

\[T_R \dfrac{\partial}{\partial T} A = j D \dfrac{\partial^2}{\partial t^2} A - j \delta |A|^2 A + (g - l)A + D_f \dfrac{\partial^2}{\partial t^2} A + \gamma |A|^2 A + L_{pert}\label{eq9.1.5} \]

Debido a los procesos irreversibles y las perturbaciones, la solución a (\(\ref{eq9.1.5}\)) es un pulso similar a un solitón con perturbaciones en amplitud, fase, frecuencia y temporización más algún continuo

\[A(t, T) = [(A_o + \Delta A_o) \text{sech} [(t - \Delta t)/\tau] + a_c (T, t)] e^{-j\phi_o T/T_R} e^{j \Delta p (T) t} e^{-j \theta_0} \nonumber \]

con energía de pulso\(w_0 = 2A_o^2 \tau\).

Las perturbaciones provocan fluctuaciones en la amplitud, fase, frecuencia central y temporización del solitón y generan radiación de fondo, es decir, continuo

\[\Delta A (T, t) = \Delta w(T) f_w (t) + \Delta \theta (T) f_{\theta} (t) + \Delta p(T) f_p (t) + \Delta t(T) f_t (t) + a_c (T, t). \nonumber \]

donde, reescribimos la perturbación de amplitud como una perturbación energética. La dinámica de los parámetros de pulso debido a la perturbada Ecuación de Schrödinger no lineal (\(\ref{eq9.1.5}\)) se puede proyectar a partir de la perturbación utilizando la base anexa y la relación de ortogonalidad, ver Capítulo 3.5. Obsérvese que el fi corresponde al primer componente del vector en Eqs. (3.5.9) - (3.5.12). La dinámica de los parámetros de pulso debido a la perturbada Ecuación de Schrödinger no lineal (\(\ref{eq9.1.5}\)) se puede proyectar a partir de la perturbación utilizando la base\(\hat{f}_i^*\) anexa correspondiente al primer componente del vector en Eqs. (3.5.31) - (3.5.34) y la nueva relación de ortogonalidad

\[\text{Re} \left \{\int_{-\infty}^{+\infty} \hat{f}_i^* (t) f_j (t) dt \right \} = \delta_{i,j}. \nonumber \]

Obtenemos

\[\dfrac{\partial}{\partial T} \Delta w = -\dfrac{1}{\tau_w} \Delta w + \dfrac{1}{T_R} \text{Re} \left \{\int_{-\infty}^{+\infty} \hat{f}_w^* (t) L_{pert} (T, t) dt \right \} \nonumber \]

\[\dfrac{\partial}{\partial T} \Delta \theta (T) = \dfrac{2\phi_o}{T_R} \dfrac{\Delta w}{w_o} + \dfrac{1}{T_R} \text{Re} \left \{\int_{-\infty}^{+\infty} \hat{f}_{\theta}^* (t) L_{pert} (T, t) dt \right \} \nonumber \]

\[\dfrac{\partial}{\partial T} \Delta p(T) = -\dfrac{1}{\tau_p} \Delta p + \dfrac{1}{T_R} \text{Re} \left \{\int_{-\infty}^{+\infty} \hat{f}_p^* (t) L_{pert} (T, t) dt \right \} \nonumber \]

\[\dfrac{\partial}{\partial T} \Delta t = \dfrac{-2|D|}{T_R} \Delta \omega + \dfrac{1}{T_R} \text{Re} \left \{\int_{-\infty}^{+\infty} \hat{f}_t^* (t) L_{pert} (T, t) dt \right \} \nonumber \]

Tenga en cuenta que la dinámica irreversible hace que el continuo generado se acople a los parámetros del solitón. Aquí, asumimos que este acoplamiento es pequeño y lo descuidamos en lo siguiente, véase [1]. Debido a la saturación de ganancia y la energía de pulso del filtro parabólico y las fluctuaciones de frecuencia central se amortiguan con constantes de decaimiento normalizadas

\[\dfrac{1}{\tau_w} = (2g_d - 2\gamma A_o^2) \nonumber \]

\[\dfrac{1}{\tau_p} = \dfrac{4}{3} \dfrac{g_s}{\Omega_g^2 \tau^2} \dfrac{1}{T_R} \nonumber \]

Aquí,\(g_s\) está la ganancia saturada y\(g_d\) se relaciona con la ganancia diferencial por

\[g_s = \dfrac{g_o}{1 + \tfrac{w_o}{P_L T_R}} \nonumber \]

\[g_d = \dfrac{dg_s}{dw_o} \cdot w_o \nonumber \]

Obsérvese, en este modelo asumimos que la ganancia sigue instantáneamente la potencia promedio intracavitaria o energía de pulso, lo cual no es cierto en general. Sin embargo, es sencillo incluir la relajación de la ganancia agregando un modelo de ganancia dinámica a las ecuaciones de perturbación. Por simplicidad vamos a descuidar esto aquí. Dado que el sistema es autónomo, no hay retiming y rephasing en el sistema de funcionamiento libre.