9.2: Ruido en los láseres de modo bloqueado
- Page ID
- 84882
Dentro de este marco se puede incluir fácilmente la respuesta del láser al ruido. El ruido de emisión espontánea debido al medio de amplificación con ganancia saturada gs y factor de ruido excesivo\(\Theta\) conduce a ruido blanco aditivo en la ecuación maestra perturbada (9.1.5) con\(L_{pert} = \xi (t, T)\), donde\(\xi\) es una fuente de ruido gaussiano blanco con función de autocorrelación
\[\langle \xi (t', T') \xi (t, T) \rangle = T_R^2 P_n \delta (t - t') \delta (T -T') \nonumber \]
donde la energía sonora de emisión espontánea\(P_n \cdot T_R\) con
\[P_n = \Theta \dfrac{2g_s}{T_R} \hbar \omega_c = \Theta \dfrac{\hbar \omega_c}{\tau_p} \nonumber \]
se agrega al pulso dentro de cada ida y vuelta en el láser. \(\tau_p\)es el tiempo de descomposición de la cavidad o la vida útil del fotón en la cavidad. Tenga en cuenta que el ruido es aproximado por ruido blanco, es decir, ruido no correlacionado en ambas escalas de tiempo\(t,T\). El ruido entre diferentes viajes de ida y vuelta ciertamente no está correlacionado. Sin embargo, el ruido blanco en la escala de tiempo rápido\(t\), asume una ganancia plana, que es una aproximación. Al proyectar las ecuaciones de movimiento para los parámetros de pulso en presencia de este ruido de acuerdo con (9.1.7) - (9.1.12), obtenemos las fuentes de ruido adicionales que están impulsando las fluctuaciones de energía, frecuencia central, sincronización y fase en el láser de modo bloqueado
\[\dfrac{\partial}{\partial T} \Delta w = -\dfrac{1}{\tau_w} \Delta w + S_w (T), \nonumber \]
\[\dfrac{\partial}{\partial T} \Delta \theta (T) = \dfrac{2\phi_o}{T_R} \dfrac{\Delta w}{w_o} \Delta w + S_{\theta} (T), \nonumber \]
\[\dfrac{\partial}{\partial T} \Delta p (T) = -\dfrac{1}{\tau_p} \Delta p + S_{p} (T), \nonumber \]
\[\dfrac{\partial}{\partial T} \Delta t= -\dfrac{2|D|}{T_R} \Delta p + S_{t} (T), \nonumber \]
con
\[S_w (T) = \dfrac{1}{T_R} \text{Re} \left \{\int_{-\infty}^{+\infty} \hat{f}_w^* (t) \xi (T, t) dt \right \}, \nonumber \]
\[S_{\theta} (T) = \dfrac{1}{T_R} \text{Re} \left \{\int_{-\infty}^{+\infty} \hat{f}_{\theta}^* (t) \xi (T, t) dt \right \}, \nonumber \]
\[S_p (T) = \dfrac{1}{T_R} \text{Re} \left \{\int_{-\infty}^{+\infty} \hat{f}_p^* (t) \xi (T, t) dt \right \}, \nonumber \]
\[S_t (T) = \dfrac{1}{T_R} \text{Re} \left \{\int_{-\infty}^{+\infty} \hat{f}_t^* (t) \xi (T, t) dt \right \}, \nonumber \]
Las nuevas fuentes de ruido reducido obedecen a las funciones de correlación
\[\langle S_w (T') S_w (T) \rangle = \dfrac{P_n}{4\omega_0} \delta (T - T'), \nonumber \]
\[\langle S_{\theta} (T') S_{\theta} (T) \rangle = \dfrac{4}{3} \left (1 + \dfrac{\pi^2}{12} \right ) \dfrac{P_n}{w_o} \delta (T - T'), \nonumber \]
\[\langle S_p (T') S_p (T) \rangle = \dfrac{4}{3} \dfrac{P_n}{w_o} \delta (T - T'), \nonumber \]
\[\langle S_t (T') S_t (T) \rangle = \dfrac{\pi^2}{3} \dfrac{P_n}{w_o} \delta (T - T'), \nonumber \]
\[\langle S_i (T') S_j (T) \rangle = 0 \text{ for } i \ne j. \nonumber \]
Los espectros de potencia de las fluctuaciones de amplitud, fase, frecuencia y temporización se definen a través de las transformadas de Fourier de las funciones de autocorrelación
\[|\Delta \hat{w} (\Omega)|^2 = \int_{-\infty}^{+\infty} \langle \Delta \hat{w} (T + \tau) \Delta \hat{w} (T) \rangle e^{-j\Omega \tau} d\tau , \text{ etc.} \nonumber \]
Después de un breve cálculo, los espectros de potencia debido al ruido del amplificador son
\[\left |\dfrac{\Delta \hat{w} (\Omega)}{w_o} \right |^2 = \dfrac{4}{1/\tau_w^2 + \Omega^2} \dfrac{P_n}{w_o},\label{eq9.2.17} \]
\[|\Delta \hat{\theta} (\Omega)|^2 = \dfrac{1}{\Omega^2} \left [\dfrac{4}{3} \left (1 + \dfrac{\pi^2}{12} \right ) \dfrac{P_n}{w_o} + \dfrac{16}{(1/\tau_p^2 + Omega^2)} \dfrac{\phi_o^2}{T_R^2} \dfrac{P_n}{w_o}\right ], \nonumber \]
\[\left |\Delta \hat{p} (\Omega) \tau \right |^2 = \dfrac{1}{1/\tau_p^2 + \Omega^2} \dfrac{4}{3} \dfrac{P_n}{w_o},\label{eq9.2.19} \]
\[\left | \dfrac{\Delta \hat{t} (\Omega)}{\tau} \right |^2 = \dfrac{1}{\Omega^2} \left [\dfrac{\pi^2}{3} \dfrac{P_n}{w_o} + \dfrac{1}{(1/\tau_{\omega}^2 + \Omega^2)} \dfrac{4}{3} \dfrac{4|D|^2}{T_R^2 \tau^4} \dfrac{P_n}{w_o} \right ]. \nonumber \]
Estas ecuaciones indican, que las fluctuaciones de energía y frecuencia central se vuelven estacionarias con fluctuaciones cuadráticas medias
\[\left \langle \left ( \dfrac{\Delta w}{w_o} \right )^2 \right \rangle = 2 \dfrac{P_n \tau_w}{w_o} \nonumber \]
\[\langle (\Delta \omega \tau )^2 \rangle = \dfrac{2}{3} \dfrac{P_n \tau_p^2}{w_o} \nonumber \]
mientras que la fase y el tiempo se someten a una caminata aleatoria con varianzas
\[\begin{array} {rcl} {\sigma_{\theta} (T)} & = & {\langle ( \Delta \theta (T) - \Delta \theta (0))^2 \rangle = \dfrac{4}{3} \left (1 + \dfrac{\pi^2}{12} \right ) \dfrac{P_n}{w_o} |T|} \\ {} & \ & {+16 \dfrac{\phi_o^2}{T_R^2} \dfrac{P_n}{w_o} \tau_p^3 \left (\exp \left [-\dfrac{|T|}{\tau_p} \right ] - 1 + \dfrac{|T|}{\tau_w} \right )} \end{array} \nonumber \]
\[\begin{array} {rcl} {\sigma_t (T)} & = & {\left \langle \left ( \dfrac{\Delta t(T) - \Delta t (0)}{\tau} \right )^2 \right \rangle = \dfrac{\pi^2}{3} \dfrac{P_n}{w_o} |T|} \\ {} & \ & {+ \dfrac{4}{3} \dfrac{4|D|^2}{T_R^2 \tau^4} \dfrac{P_n}{w_o} \tau_{\omega}^3 \left (\exp \left [-\dfrac{|T|}{\tau_p} \right ] - 1 + \dfrac{|T|}{\tau_p} \right )} \end{array} \nonumber \]
El ruido de fase provoca el ancho finito fundamental de cada línea del peine de modo bloqueado en el dominio óptico. La fluctuación de tiempo conduce a un ancho de línea finito de la señal de microondas detectada, que es equivalente a las fluctuaciones fundamentales de los láseres en la tasa de repetición. En el sentido estricto, la fase y la sincronización en un láser de modo bloqueado de funcionamiento libre (u oscilador autónomo) ya no son procesos estacionarios. Sin embargo, como sabemos que se trata de variables distribuidas gaussianas, podemos calcular los espectros de amplitud de los fasores sometidos a procesos de difusión de fase con bastante facilidad. La diferencia de fase\(\varphi = \Delta \theta (T) - \Delta \theta (0)\) es una variable distribuida gaussiana con varianza σ y distribución de propabilidad
\[p(\varphi) = \dfrac{1}{\sqrt{2\pi \sigma}} e^{-\tfrac{\varphi^2}{2\sigma}}, \text{ with } \sigma = \langle \varphi^2 \rangle. \nonumber \]
Por lo tanto, el valor de expectativa de un fasor con fase\(\phi\) es
\[\begin{array} {rcl} {\langle e^{j\varphi} \rangle} & = & {\dfrac{1}{\sqrt{2\pi \sigma}} \int_{-\infty}^{+\infty} e^{-\tfrac{\varphi^2}{2\sigma}} e^{j \varphi} d \varphi} \\ {} & = & {e^{-\tfrac{1}{2} \sigma}} \end{array}\label{eq9.2.26} \]
Espectro óptico
\[a(t, T) = \left (A_0 \text{sech} (\dfrac{t - t_0}{\tau}) + a_c (T, t) \right ) e^{-j \phi_0 \tfrac{T}{T_R}} \nonumber \]
En presencia de ruido la salida del láser cambia de eq. (9.1) a un proceso aleatorio. Despreciando el continuo de fondo obtenemos:
\[\begin{array} {c} {A(t, T = m T_R) = \sum_{m = -\infty}^{+\infty} (A_0 + \Delta A(m T_R)) \text{sech } \left (\dfrac{t - mT_R - \Delta t (mT_R)}{\tau} \right ) } \\ {e^{j \Delta \phi_{CE} \cdot m} e^{j(\omega_c + \Delta p (mT_R)) t} e^{-j\Delta \theta (mT_R)}} \end{array}\label{eq9.2.28} \]
Por simplicidad, descuidaremos en las siguientes fluctuaciones de amplitud y frecuencia portadora en la Ec. (\(\ref{eq9.2.28}\)), porque están acotados y se vuelven solo importantes en grandes compensaciones del peine. Sin embargo, los mantenemos en las expresiones para las Eqs de jitter de fase y temporización. (\(\ref{eq9.2.17}\)) y (\(\ref{eq9.2.19}\)). Asumimos un proceso estacionario, de modo que el espectro de potencia óptica se puede calcular a partir de
\[S(\omega) = \lim_{T = 2NT_R \to \infty} \dfrac{1}{T} \langle \hat{A}_T^* (\omega) \hat{A}_T (\omega) \rangle\label{eq9.2.29} \]
con los espectros relacionados con un intervalo de tiempo finito
\[\begin{array} {rcl} {\hat{A}_T (\omega) = \int_{-T}^T A(t) e^{-j \omega t} dt} & = & {\hat{a}_0 (\omega - \omega_c) \sum_{m = -N}^{N} e^{jmT_R (\tfrac{\Delta \phi_{CE}}{T_R} - \omega)}} \\ {} & \ & {e^{-j[(\omega - \omega_c)\Delta t (mT_R) + \Delta \theta (mT_R)]}} \end{array} \nonumber \]
donde\(\hat{a}_0 (\omega)\) está la transformada de Fourier de la forma del pulso. En este caso
\[\hat{a}_0 (\omega) = \int_{-\infty}^{\infty} A_0 \text{sech} (\dfrac{t}{\tau}) e^{-j \omega t} dt = A_0 \pi \tau \text{sech} (\dfrac{\pi}{2} \omega \tau) \nonumber \]
Con (\(\ref{eq9.2.29}\)) el espectro óptico del láser viene dado por
\[\begin{array} {rcl} {S(\omega)} & = & {\lim_{N \to \infty} |\hat{a}_0 (\omega - \omega_c)|^2 \dfrac{1}{2NT_R} \sum_{m' = -N}^{N} \sum_{m = -N}^{M} e^{j T_R (\tfrac{\phi_{CE}}{T_R} - \omega)(m - m')}} \\ {} & \ & {\langle e^{+j [2\pi (f - f_c) (\Delta t (mT_R) - \Delta t (m'T_R)) - (\theta (m T_R) - \theta (m' T_R))]} \rangle} \end{array} \nonumber \]
Tenga en cuenta, que la diferencia entre las fases y el tiempo sólo depende de la diferencia\(k = m−m'\). En el modelo actual las fluctuaciones de fase y sincronización no están correlacionadas. Por lo tanto, para\(N \to \infty\) obtener
\[\begin{array} {rcl} {S(\omega)} & = & {|\hat{a}_0 (\omega - \omega_c)|^2 \tfrac{1}{T_R} \sum_{k' = -\infty}^{\infty} e^{jT_R (\tfrac{\Delta \phi_{CE}}{T_R} - \omega) k}} \\ {} & \ & {\langle e^{+j[2\pi (\omega - \omega_0)(\Delta t ((m + k) T_R) - \Delta t (m T_R))]} \rangle \langle e^{-j (\theta ((m + k) T_R) - \theta (m T_R))} \rangle} \end{array} \nonumber \]
Los valores de expectativa son exactamente del tipo calculado en (\(\ref{eq9.2.26}\)), lo que lleva a
\[\begin{array} {rcl} {S(\omega)} & = & {\dfrac{|\hat{a}_0 (\omega - \omega_c)|^2}{T_R} \sum_{k' = -\infty}^{\infty} e^{jT_R (\tfrac{\phi_{CE}}{T_R} - \omega)k} e^{-\tfrac{1}{2} \sigma_{\theta} (kT_R)}} \\ {} & \ & {e^{-\tfrac{1}{2} [((\omega - \omega_c)\tau)^2 \sigma_t (kT_R)]}} \end{array}\label{eq9.2.34} \]
La mayoría de las veces nos interesa el ruido muy cercano a las líneas en desplazamientos de frecuencia mucho más pequeños que los tiempos de relajación de energía inversa y frecuencia\(\tau_w\) y\(\tau_p\). Esto está determinado por el comportamiento a largo plazo de las varianzas, que crecen linealmente en\(|T|\)
\[\sigma_{\theta} (T) = \dfrac{4}{3} \left (1 + \dfrac{\pi^2}{12} + 16 \dfrac{\tau_w^2}{T_R^2} \phi_o^2 \right ) \dfrac{P_n}{w_o} |T| = 2 \Delta \omega_{\phi} |T|, \nonumber \]
\[\sigma_t (T) = \dfrac{1}{3} \left (\pi^2 + \dfrac{\tau_p^2}{T_R^2} \left (\dfrac{D}{\tau^2} \right )^2 \right ) \dfrac{P_n}{w_o} |T| = 4 \Delta \omega_t |T|, \nonumber \]
con las tarifas
\[\Delta \omega_{\phi} = \dfrac{2}{3} \left (1 + \dfrac{\pi^2}{12} + 16 \dfrac{\tau_w^2}{T_R^2} \phi_o^2 \right ) \dfrac{P_n}{w_o},\label{eq9.2.37} \]
\[\Delta \omega_t = \dfrac{1}{6} \left (\pi^2 + \dfrac{\tau_p^2}{T_R^2} \left (\dfrac{D}{\tau^2} \right )^2 \right ) \dfrac{P_n}{w_o}.\label{eq9.2.38} \]
De la fórmula de Poisson
\[\sum_{k = -\infty}^{+ \infty} h[k] e^{-j kx} = \sum_{n = -\infty}^{+\infty} G(x + 2n\pi) \nonumber \]
donde
\[G(x) = \int_{-\infty}^{+\infty} h[k] e^{-jkx} dk, \nonumber \]
y Eqs. (\(\ref{eq9.2.34}\)) a (\(\ref{eq9.2.38}\)) finalmente llegamos al espectro de línea óptica del láser de modo bloqueado
\[S(\omega) = \dfrac{|\hat{a}_0 (\omega - \omega_c)|^2}{T_R^2} \sum_{n = -\infty}^{+\infty} \dfrac{2\Delta \omega_n}{(\omega - \omega_n)^2 + \Delta \omega_n^2} \nonumber \]
que son líneas lorentzianas en las posiciones de peine de modo.
\[\omega_n = \omega_c + n \omega_R - \dfrac{\Delta \phi_{CE}}{T_R}, \nonumber \]
\[= \dfrac{\Delta \phi_{CE}}{T_R} + n_R' \omega, \nonumber \]
con un ancho medio a la mitad máximo de
\[\Delta \omega_n = \Delta \omega_{\phi} + [\tau (\omega_n - \omega_c)]^2 \Delta \omega_t. \nonumber \]
Estimar el número de modos M incluidos en el peine
\[M = \dfrac{T_R}{\tau}, \nonumber \]
vemos que la contribución de las fluctuaciones de tiempo al ancho de línea de las líneas de peine en el centro del peine es insignificante. Así, el ancho de línea del peine en el centro viene dado por (\(\ref{eq9.2.37}\))
\[\Delta \omega_{\phi} = \dfrac{2}{3} \left (1 + \dfrac{\pi^2}{12} + 16 \dfrac{\tau_w^2}{T_R^2} \phi_o^2 \right ) \dfrac{\Theta 2 g_s}{N_0 T_R} \nonumber \]
\[\dfrac{2}{3} \left (1 + \dfrac{\pi^2}{12} + 16 \dfrac{\tau_w^2}{T_R^2} \phi_o^2 \right ) \dfrac{\Theta}{N_0 \tau_p} \nonumber \]
donde\(N_0 = \tfrac{w_o}{\hbar \omega_c}\) es el número de fotones en la cavidad y\(\tau_p = T_R /(2l)\) es la vida útil de los fotones en la cavidad. Tenga en cuenta que este resultado para el láser de modo bloqueado está estrechamente relacionado con el ancho de línea de Schawlow-Towns de un láser de onda continua que es\(\Delta f_{\phi} = \tfrac{\Theta}{2\pi N_0 \tau_p}\). Para un láser de estado sólido a alrededor de la longitud de\(1\mu m\) onda con una energía de pulso intracavitaria típica de 50 nJ correspondiente a\(N_0 = 2.5 \cdot 10^{11}\) fotones y tasa de repetición de 100 MHz con un acoplador de salida del 10% y una cifra de ruido en exceso de\(\Theta = 2\), se obtiene\(\Delta f_{\phi}^{\sim} \tfrac{\Theta}{3\pi N_0 \tau_p} = 8\mu Hz\) sin el término de conversión de amplitud a fase dependiendo del desplazamiento de fase no lineal\(\phi_o\). Estos anchos de línea intrínsecos se deben a fluctuaciones que ocurren en una escala de tiempo más rápida que el tiempo de ida y vuelta y, por lo tanto, no pueden ser compensados por mecanismos de servocontrol externos. Para los láseres sub-10 fs, los espectros llenan el ancho de banda de ganancia completa y el KLM es bastante fuerte, de modo que los tiempos de relajación de amplitud y frecuencia central son del orden de 10-100 recorridos de ida y vuelta de cavidad. En los láseres TI:zafiro de pulso muy corto, los desplazamientos de fase no lineales son del orden de 1 rad por ida y vuelta. Entonces la mayoría de las fluctuaciones se deben a fluctuaciones de amplitud convertidas en fluctuación de fase. Estas contribuciones pueden aumentar el ancho de línea en un factor de 100-10000, lo que puede llevar el ancho de línea al nivel de MHz y Hz.
Espectro de microondas
No solo el espectro óptico es de interés como el espectro de la salida fotodetectada del láser es de interés. La detección de fotos simple puede convertir la corriente de pulsos ópticos de baja fluctuación en un peine de señales de microondas de ruido de fase extremadamente bajo. La corriente del fotodetector es proporcional a la potencia de salida del láser. De la Eq. (\(\ref{eq9.2.28}\)) encontramos
\[\begin{array} {rcl} {I(t)} & = & {\eta \dfrac{e}{\hbar \omega_c} |A(T, t)|^3 = \eta \dfrac{e}{\hbar \omega_c \tau} \times } \\ {} & \ & {\sum_{m = -\infty}^{+\infty} (w_0 + \Delta w (mT_R)) \dfrac{1}{2} \text{sech}^2 \left (\dfrac{t - mT_R - \Delta t (mT_R)}{\tau} \right ),} \end{array} \nonumber \]
donde\(\eta\) está la eficiencia cuántica. Por simplicidad volvemos a descuidar el ruido de amplitud y considerar solo las consecuencias debido a la fluctuación de tiempo. Luego obtenemos para la Transformada de Fourier de la foto actual
\[\hat{I}_T (\omega) = \eta \dfrac{ew_0}{\hbar \omega_0 \tau} |a_0|^2 (\omega) \sum_{m =-N}^{+N} e^{-j \omega (mT_R + \Delta t (mT_R))}, \nonumber \]
\[|a_0|^2 (\omega) = \int_{-\infty}^{\infty} \dfrac{1}{2} \text{sech}^2 (x) e^{-\omega \tau x} dx \nonumber \]
\[= \dfrac{\pi \omega \tau}{\text{sinh} (\tfrac{\pi}{2} \omega \tau)}, \nonumber \]
y su espectro de potencia de acuerdo con la Ec. (\(\ref{eq9.2.29}\))
\[\begin{array} {rcl} {S_I (\omega)} & = & {\dfrac{(\eta e N_0)^2}{T_R} ||a_0|^2 (\omega)|^2 \sum_{k = -\infty}^{+ \infty} e^{-j \omega k T_R} \langle e^{-j\omega (\Delta t (k T_R) - \Delta t (0))} \rangle,} \\ {} & = & {\dfrac{(\eta e N_0)^2}{T_R} ||a_0|^2 (\omega)|^2 \sum_{k = -\infty}^{+ \infty} e^{-j \omega k T_R} e^{-\tfrac{1}{2}[(\omega \tau)^2 \sigma_t (kT_R)]}} \end{array} \nonumber \]
El uso de la fórmula de Poisson nuevamente da como resultado
\[\begin{array} {rcl} {S_I (\omega)} & = & {\dfrac{(\eta e N_0)^2}{T_R} ||a_0|^2 (\omega)|^2 \sum_{k = -\infty}^{+ \infty} e^{-j \omega k T_R} e^{-j\omega (\Delta t (k T_R) - \Delta t (0))},} \\ {} & = & {\dfrac{(\eta e N_0)^2}{T_R} ||a_0|^2 (\omega)|^2 \sum_{k = -\infty}^{+ \infty} \dfrac{2\Delta \omega_{I,n}}{(\omega - n \omega_R)^2 + \Delta \omega_{I,n}^2}} \end{array} \nonumber \]
con el ancho\(\Delta \omega_{I,n}\) de línea de la enésima armónica
\[\begin{array} {rcl} {\Delta \omega_{I,n}} & = & {\left (2\pi n \dfrac{\tau}{T_R} \right )^2 \Delta \omega_t} \\ {} & = & {\left (\dfrac{2\pi n}{M} \right )^2 \Delta \omega_t} \end{array} \nonumber \]
La línea fundamental\((n = 1)\) del espectro de microondas tiene un ancho que es\(M^2\) −veces menor que el ancho de línea óptico. Para un láser de 10-fs con tasa de repetición de 100 MHz, el número de modos\(M\) es de aproximadamente un millón.
Ejemplo: láser de fibra YB
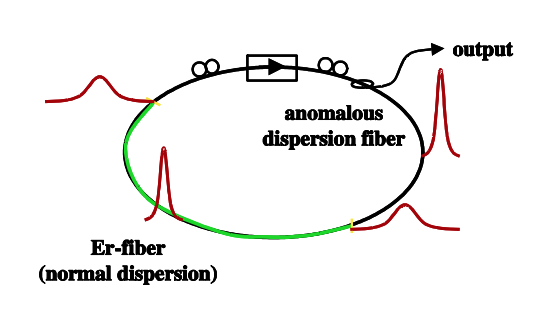
La Figura 9.3 muestra el esquema de un láser modelobloqueado de pulso estirado que opera cerca de dispersión cero. Por lo tanto, se debe minimizar la contribución del jitter de Gordon-Haus. De hecho, se ha demostrado y discutido que este tipo de láseres alcanzan niveles mínimos de jitter [2] [3] [4].
La fluctuación de tiempo del láser de pulso estirado que se muestra en la Figura se calcula en la tabla 9.1.
Los resultados teóricos anteriores se derivan con la teoría de perturbación de solitones. El láser modelobloqueado de pulso estirado en la Figura 9.3 en realidad está lejos de ser un láser solitón, ver [3] [4]. El pulso respira considerablemente durante
| Ganancia Medio Ancho Medio Máximo | \(\Omega_g = 2\pi \cdot \tfrac{0.3 \mu m/fs}{(1 \mu m)^2} 0.02 \mu m = 38 THz\) |
| Ganancia saturada | \(g_s = 1.2\) |
| Ancho de pulso | \(\tau_{FWHM} = 50fs, \tau = \tau_{FWHM}/1.76 = 30fs\) |
| Tiempo de repetición de pulso | \(T_R = 12 ns\) |
| Tiempo de decaimiento para fluctuaciones de frecuencia central | \(\tfrac{1}{\tau_p} = \tfrac{4}{3} \tfrac{g_s}{\Omega_g^2 \tau^2 T_R} = \tfrac{4}{3} \tfrac{1}{T_R}\) |
| Poder intracavitario | \(P = 100 mW\) |
| Energía de pulso intra cavidad /número de fotones | \(w_o = 1.2nJ, N_0 = 0.6 \cdot 10^{10}\) |
| Densidad espectral de potencia de ruido | \(P_n = \Theta \tfrac{2g_s}{T_R} \hbar w_o\) |
| Factor de exceso de ruido del amplificador | \(\Theta = 10\) |
| Ruido ASE | \(\tfrac{P_n}{w_o} = \Theta \tfrac{2g_s}{T_R N_0} = \tfrac{1}{3} Hz\) |
| Dispersión | \(5000 fs^2\) |
| Conv de frecuencia a sincronización | \(\tfrac{4}{\pi^2} \tfrac{4|D|^2}{\tau^4} \tfrac{\tau_p^2}{T_R^2} = (\tfrac{2}{\pi} \tfrac{3}{4} \tfrac{3 \cdot 10000}{1000})^2 = (3.7)^2\) |
| Densidad de fluctuación de sincronización | \(|\tfrac{\Delta \hat{t} (\Omega)}{\tau}|^2 = \tfrac{1}{\Omega^2} \tfrac{\pi^2}{3} \tfrac{P_n}{w_o} (1 + \tfrac{4}{\pi^2} \tfrac{4|D|^2}{\tau^4} \tfrac{1}{(T_R^2/\tau_p^2 + T_R^2 \Omega^2)})\) |
| Jitter de sincronización\([f_{\min},f_{\max}]\) para\(f_{\min} << 1/\tau_p\)\(f_{\min} = 10kHz\),\(D = 5000 fs^2\) | \(\Delta t = \tau \sqrt{\tfrac{1}{12 \cdot f_{\min}} \tfrac{P_n}{w_o} (1 + \tfrac{4}{\pi^2} \tfrac{4|D|^2}{\tau^4} \tfrac{\tau_p^2}{T_R^2})} = 0.2 fs\) |
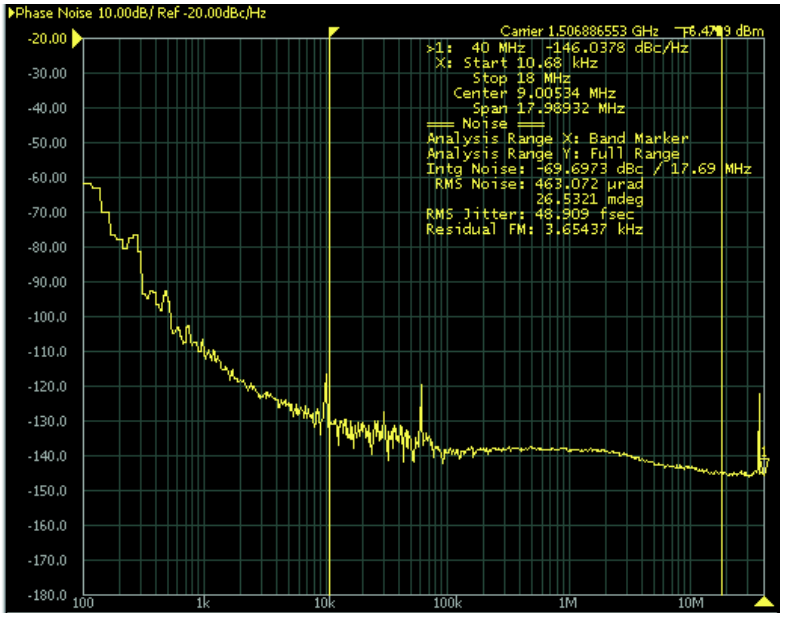
paso a través de la cavidad hasta un factor de 10. Por lo tanto, la teoría debe tomarlo en cuenta asumiendo un ancho de pulso promedio cuando se agrega el ruido en la cavidad. Para más detalles véase [3] [4]. En realidad, estos anchos de línea cuánticos limitados (ASE) y bastante pequeños ópticos y de microondas son difíciles de observar, ya que en la mayoría de los casos se ven inundados por ruidos técnicos como las fluctuaciones en la potencia de la bomba, que pueden dar lugar a fluctuaciones de ganancia, o vibraciones de espejo, fluctuaciones de densidad de aire o derivas térmicas, que causar directamente cambios en la tasa de repetición de los láseres. La Figura 9.4 muestra el espectro de ruido de fase de banda lateral única\(L(f)\) del armónico N=32nd de la tasa de repetición fundamental, es decir 1.3 GHz, en el espectro de fotocorriente 9.70. La fase del armónico N=32nd de la fotocorriente 9.65 está directamente relacionada con la fluctuación de tiempo por
\[\Delta \phi (T) = 2\pi Nf_R \Delta t (T) \nonumber \]
El ruido de fase de banda lateral única es la densidad espectral de potencia de estas fluctuaciones de fase definida de la misma manera que la densidad espectral de potencia de la propia fotocorriente, i.e.
\[L(f) = 2\pi S_{\Delta \phi} (\omega) \nonumber \]
Las fluctuaciones de fase en un cierto intervalo de frecuencia se pueden evaluar fácilmente mediante
\[\Delta \phi^2 = 2\int_{f_{\min}}^{f_{\max}} L(f) df. \nonumber \]
Y la fluctuación de tiempo es entonces
\[\Delta t = \dfrac{1}{2\pi Nf_R} \sqrt{2 \int_{f_{\min}}^{f_{\max}} L(f) df} \nonumber \]
Para las mediciones que se muestran en la Figura 9.4 se obtiene para la fluctuación de temporización integrada de 10kHz a 20 MHz de 50 fs. Esto es aproximadamente 200 veces mayor que los límites derivados en la tabla 9.1. Esta discrepancia proviene de varios efectos, lo más notable la conversión de amplitud a fase en el fotodetector durante la fotodetección, un efecto aún no bien entendido así como otras fuentes de ruido que podríamos no haber modelado, como el ruido del láser de la bomba. Sin embargo, estas fuentes de ruido pueden eliminarse en principio mediante un diseño cuidadoso y bucles de retroalimentación. Por lo tanto, es importante entender la dependencia del grupo y la velocidad de fase de la potencia intracavitaria o energía de pulso al menos dentro del modelo básico actual. Los efectos lineales y no lineales adicionales debido a la dispersión lineal de orden superior o no linealidades pueden causar cambios adicionales en la velocidad de grupo y fase, lo que también podría crear dependencias inusuales de la velocidad de grupo y fase en la energía del pulso intracavitario. Aquí discutimos como ejemplo el impacto del efecto Kerr instantáneo en la velocidad de grupo y fase de un pulso similar a un solitón.