9.4: Peines de Frecuencia Láser de Femtosegundo
- Page ID
- 84872
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sin embargo, la fórmula (9.3.7) puede ser utilizada para el control del peine de frecuencia óptica de un láser de femtosegundos mediante el control de la longitud de la cavidad y la energía del pulso intracavidad, a través de la potencia de la bomba. Según la Figura 9.2 cada línea del peine óptico determinada por
\[f_m = f_{CE} + mf_R. \nonumber \]
Tenga en cuenta que si el láser de femtosegundos emite un espectro que cubre más de una octava, entonces se puede frecuentar doble parte del peine a bajas frecuencias y golpearlo con la parte de alta frecuencia correspondiente del peine en un fotodetector, ver Figura 9.5 El resultado es una señal de latido fotodector que consiste en discreta líneas en las frecuencias de latido
\[f_k = kf_R \pm f_{CE} \nonumber \]
Este método para determinar la frecuencia de desplazamiento de envolvente portadora se denomina interferometría f a 2f. La frecuencia de desplazamiento de envolvente portadora se puede extraer con filtros y sincronizarse con un oscilador local o con una fracción de la tasa de repetición del láser, por ejemplo\(f_R/4\).
La Figura 9.6 muestra la configuración de un láser de octava que abarca 200 MHz TI:zafiro donde la frecuencia de desplazamiento de envolvente de portadora\(f_{CE}\) se bloquea a un oscilador local a 36 MHz usando el método de autorreferencia f-a-2f [6]
La salida espectral de este láser se muestra en la Figura 9.7. Los componentes espectrales en 1140 se retrasan adecuadamente en una línea de retardo de espejo chirped contra los componentes espectrales a 570 nm. El rango de 1140 nm se duplica en frecuencia en un cristal BBO de 1mm y la frecuencia duplicó la luz junto con
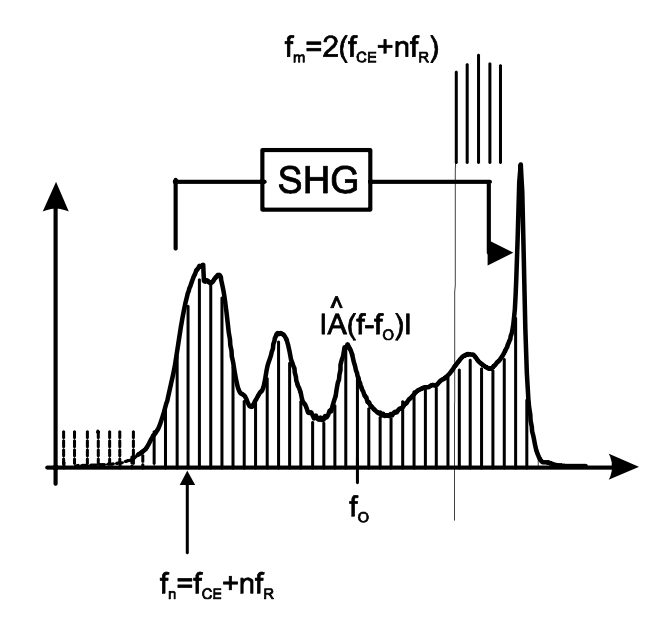
Imagen eliminada debido a restricciones de derechos de autor.
Por favor vea:
Mucke, Oliver, et al. “Ti Auto-Referenciado de 200 MHz que abarca octavas: Láser de zafiro con fluctuación de fase de envolvente de portadora de 50 attosegundos”. Optics Express 13, núm. 13 (junio de 2005): 5163-5169.
Figura 9.6: Láser TI:zafiro de expansión de octavas de 200 MHz estabilizado en fase de envolvente portadora. El propio láser de femtosegundos se encuentra dentro de la zona gris. AOM, modulador acusto-óptico; S, espejo final plateado; OC, espejo de acoplamiento de salida; PBS, cubo divisor de haz polarizador; PMT, tubo fotomultiplicador; PD, detector de fase digital; LF, filtro de bucle; VSA, analizador de señales vectoriales. La frecuencia de envolvente de portadora está bloqueada en fase a 36 MHz.
Imagen eliminada debido a restricciones de derechos de autor.
Por favor vea:
Mucke, Oliver, et al. “Ti Auto-Referenciado de 200 MHz que abarca octavas: Láser de zafiro con fluctuación de fase de envolvente de portadora de 50 attosegundos”. Optics Express 13, núm. 13 (junio de 2005): 5163-5169. Usado con permiso.
Figura 9.7: Espectro de salida del láser Ti:zafiro en una escala lineal (curva negra) y en una escala logarítmica (curva gris). Las longitudes de onda 570 y 1140 nm utilizadas para la autorreferencia se indican mediante dos líneas discontinuas.
Imagen eliminada debido a restricciones de derechos de autor.
Por favor vea:
Mucke, Oliver, et al. “Ti Auto-Referenciado de 200 MHz que abarca octavas: Láser de zafiro con fluctuación de fase de envolvente de portadora de 50 attosegundos”. Optics Express 13, núm. 13 (junio de 2005): 5163-5169.
Figura 9.8: Espectro de potencia de radiofrecuencia medido con un ancho de banda de resolución de 100 kHz (RBW). El pico en la frecuencia de desplazamiento de frecuencia de envolvente portadora exhibe una relación señal/ruido de ~35 dB.
el fundamental a 570 nm se proyecta en la misma polarización a través de un divisor de haz polarizador. Luego se filtra la señal a través de un filtro de 10nm de ancho y se detecta con un tubo fotomultiplicador (PMT). Una señal típica del PMT se muestra en la Figura 9.8.El bloqueo de fase se logra mediante un bucle de bloqueo de fase (PLL) alimentando la señal de error del detector de fase digital a un AOM colocado en el haz de la bomba (ver Figura 9.6) que modula la potencia de la bomba y, por lo tanto, cambia la frecuencia de envolvente portadora a través de la Ec. (9.82). Se utiliza un filtro de paso de banda para seleccionar la señal de latido de envolvente de portadora a 170 MHz. Esta señal es amplificada, dividida por 16 en frecuencia, y comparada con una frecuencia de referencia fLO suministrada por un generador de señal (Agilent 33250A) utilizando un detector de fase digital. La señal de latido de envolvente portadora se divide por 16 para mejorar el rango de bloqueo del PLL. El detector de fase actúa como un discriminador de frecuencia cuando el bucle está abierto, la salida es así la diferencia de frecuencia entre la frecuencia de envolvente portadora y la frecuencia de bloqueo designada. La señal de salida se amplifica en el filtro de bucle, que en nuestro caso es un controlador proporcional e integral, y se retroalimenta al AOM, cerrando el bucle. La salida del detector de fase es proporcional a la fluctuación restante entre la evolución de fase de la envolvente de portadora y el oscilador local reducida por la relación de división 16. La densidad espectral de potencia (PSD) de las fluctuaciones de fase de envolvente portadora se mide con un analizador de señales vectoriales (VSA) a la salida del detector de fase. Después de una reescalación apropiada por el factor de división, el error de fase PSD se muestra en la Figura 9.9. La medición se realizó en pasos con igual cantidad de puntos por década. El PSD de las fluctuaciones de fase de envolvente de portadora se puede integrar para obtener el error de fase total. En el rango por encima de 1 MHz (ver Figura 9.9), el acu- racy de esta medición está limitado por el piso de ruido del analizador de señales vectoriales. Obtenemos una fluctuación de fase de envolvente de portadora integrada de aproximadamente 0.1 radián en el rango de frecuencia medido. La mayor contribución al ruido de fase proviene de las fluctuaciones de baja frecuencia <10 kHz. Si además de la frecuencia de envolvente portadora también la tasa de repetición del láser se bloquea a un estándar de frecuencia, tal como por ejemplo un reloj de Cesio, el peine de frecuencia láser de femtosegundos en el dominio óptico se determina completamente con precisión de microondas y se puede usar para frecuencia óptica mediciones [6].
Imagen eliminada debido a restricciones de derechos de autor.
Por favor vea:
Mucke, Oliver, et al. “Ti Auto-Referenciado de 200 MHz Octave-Spanning: Láser de Zafiro con 50 Attosegundos
Jitter de fase de envolvente de portadora”. Optics Express 13, núm. 13 (junio de 2005): 5163-5169.
Figura 9.9: Densidad espectral de potencia de ruido de fase de envolvente de portadora (izquierda) y fluctuación de fase integrada (derecha) dando como resultado solo 45 como fluctuación de temporización de envolvente portadora acumulada.
Bibliografía
[1] H.A. Haus y A. Mecozzi: Ruido de láseres de modo bloqueado, IEEE J. Quan- tum Electron. 29, 983-996 (1993).
[2] S. Namiki y H. A. Haus: “Observación de jitter de tim- ing casi quantum-limited en un láser P-APM de anillo todo de fibra”, J. del Opt. Soc. de Am. B., 13, 2817-2823 (1996).
[3] S. Namiki y H. A. Haus: “Ruido del láser de anillo de fibra de pulso estirado: Parte I—Teoría”, IEEE J. de Quantum Electronics, 33, 640-659 (1997).
[4] Ch. Xu, S. Namiki, H. A. Haus: “Ruido en el láser de fibra de pulso rayado: Parte II — Experimentos”, IEEE J. de Quantum Electronics, 33, 660-668 (1997).
[5] H.A. Haus y E.P. Ippen: Velocidad de grupo de solitones, Opt. Let. 26, 1654-1656 (2001)
[6] D. J. Jones, S. A. Diddams, J. K. Ranka, R. S. Windeler, J. L. Hall, y S. T. Cundiff, Ciencia 288, 635 (2000).


