11.1: Mediciones de Sonda de Bomba
- Page ID
- 84871
11.1.1 Mediciones de sonda de bomba no colineal
La Figura 11.1 muestra una configuración de medición de bomba-sonda no colineal. Para suprimir la luz de fondo y el ruido de baja frecuencia del haz de la sonda, el haz de la bomba se pica. Las frecuencias típicas de los picadores mecánicos regulares son\(f_{ch} = 100Hz − 2kHz\). Se han construido picadoras mecánicas de hasta 20kHz. Con moduladores acústico-ópticos o moduladores electro-ópticos son posibles frecuencias chopper de hasta varios cientos de MHz.
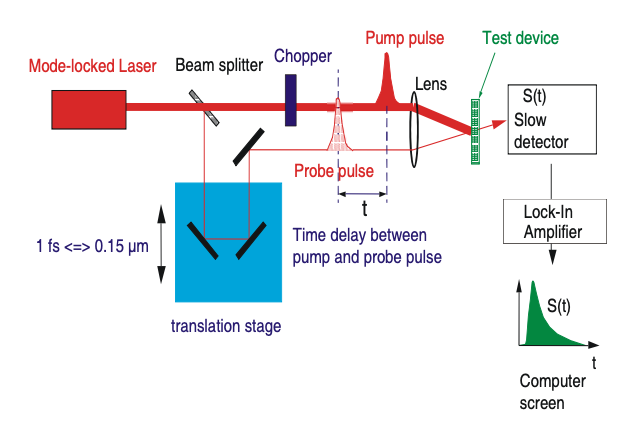
Permite denotar\(S_{in} = S_0 + \delta S\) como la energía de pulso de sonda, donde\(S_0\) está el valor promedio y\(\delta_s\) un ruido de baja frecuencia de la fuente de pulso y\(S(t)\) es la señal de sonda transmitida a través del dispositivo de prueba. Entonces la señal detectada transmitida a través del dispositivo de prueba se puede escribir como
\[\begin{array} {rcl} {S(t)} & = & {T(P(t)) S_{in}} \\ {} & = & {T_0 S_{in} + \dfrac{dT}{dP} (P_0 m (t))} \end{array} \nonumber \]
donde\(T_0\) esta la transmisión sin pulso de bomba, P0 es la energía del pulso de la bomba y\(m(t)\) la función de modulación chopper. Es obvio que si el ruido del láser de sonda\(\delta S\) es de baja frecuencia, entonces la señal se puede alejar de este piso de ruido seleccionando una frecuencia de corte apropiadamente grande en\(m(t)\). Idealmente, la frecuencia del helicóptero se elige lo suficientemente grande como para permitir la detección limitada de ruido de disparo.
A veces, los dispositivos de prueba o las muestras tienen una superficie rugosa y la luz de la bomba dispersada desde la superficie podría golpear el detector. Esto se puede suprimir parcialmente mediante la polarización ortogonal de la bomba y la sonda
Esta es una técnica estándar para comprender la dinámica de relajación en la materia condensada, como los procesos de relajación de portadores en semiconductores, por ejemplo.
Medición colineal de la bomba-Sonda:
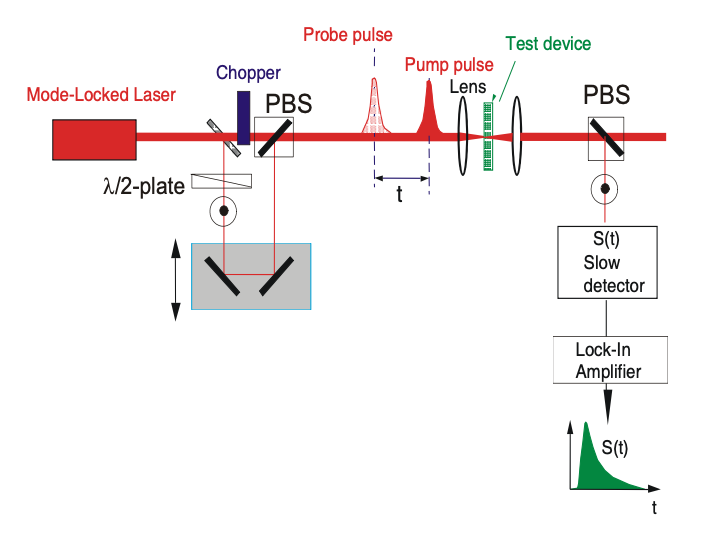
A veces, los pulsos de bomba y sonda tienen que ser colineales, por ejemplo, cuando se tienen que realizar mediciones de sonda de bomba de dispositivos de guía de ondas. Luego, el pulso de la bomba y la sonda, que podrían estar ambos en la misma longitud de onda central, deben hacerse separables. Esto se puede lograr mediante el uso de polarización ortogonal de bomba y sonda como se muestra en la Figura 11.2 o cortando la bomba y la sonda a diferentes frecuencias y detectando a la frecuencia de diferencia, ver Figura 11.3.
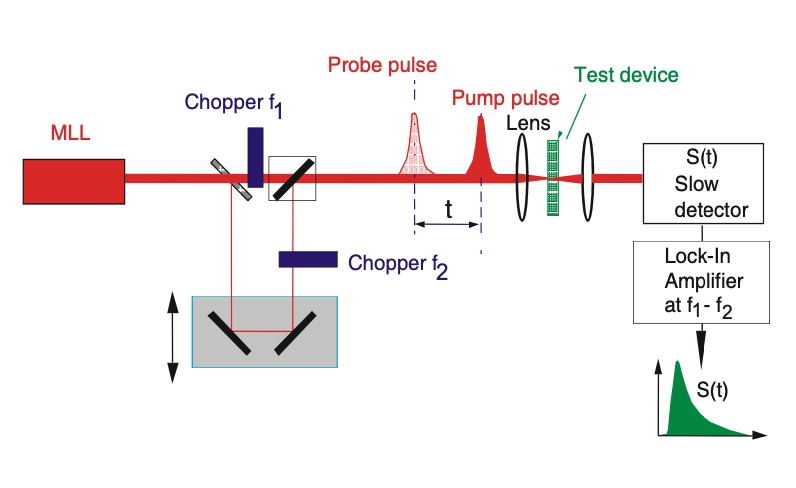
Sonda de Bomba Heterodina
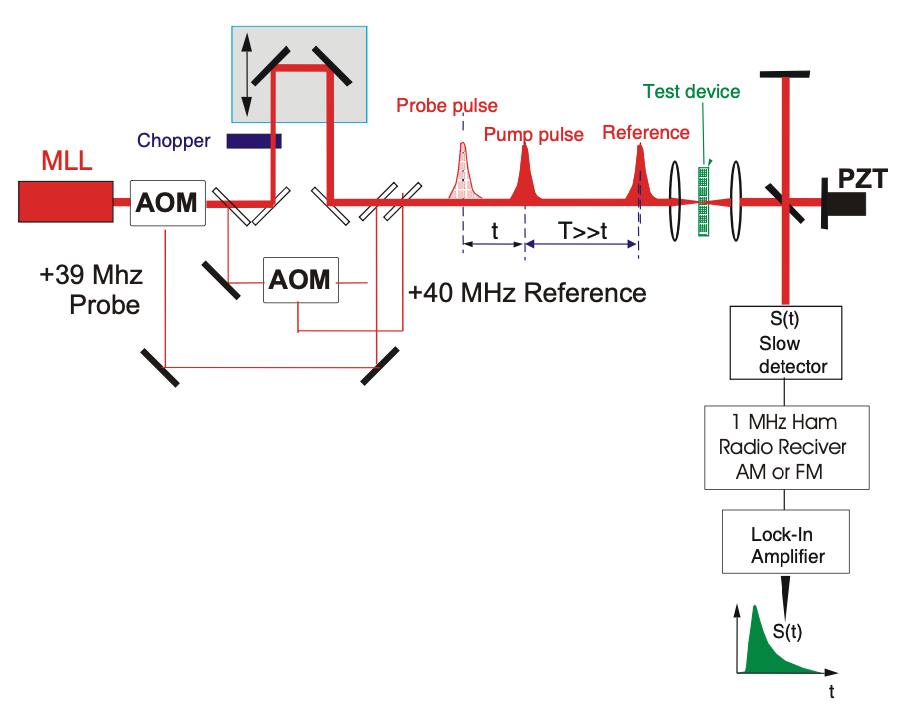
La detección de bloqueo se mejora mucho si la frecuencia de diferencia a la que se produce la detección se puede elegir más alta y la señal se puede filtrar mucho mejor usando un receptor heterodino. Esto se muestra en la Figura 11.4, donde se utilizan AOM para preparar una sonda y un desplazamiento de pulso de referencia por 39 y 40 MHz respectivamente. El haz de la bomba se pica a 1 kHz. Después del dispositivo de prueba, la sonda y el pulso de referencia se superponen entre sí retrasando el pulso de referencia en un Interferómetro Michelson. La nota de latido a 1MHz se convierte descendentemente a banda base con un receptor.
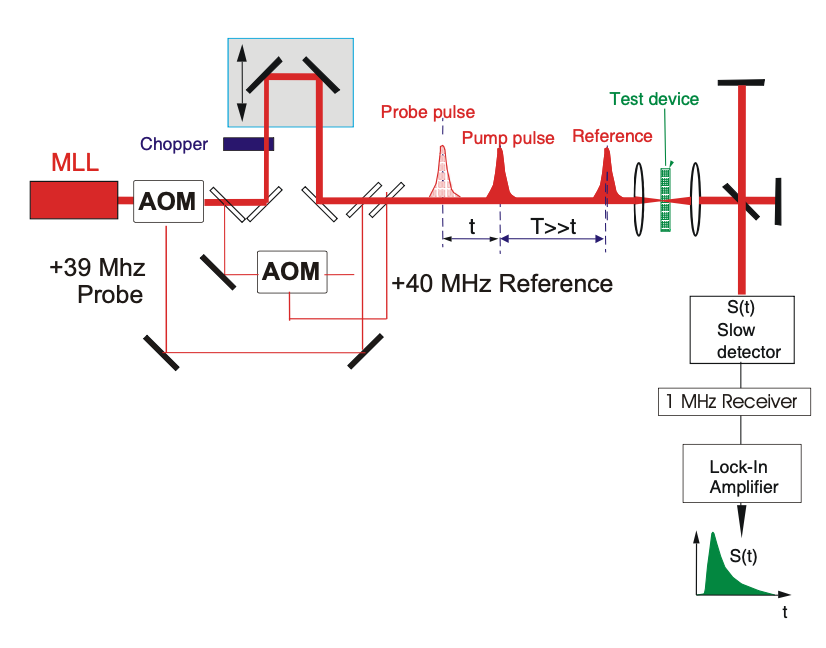
Si se utiliza un receptor AM o FM y los interferómetros que generan el pulso de referencia y sonda son interferométricamente estables, tanto las no linealidades de amplitud como de fase pueden detectarse con alta señal a ruido.