1.2: Formas de onda sinusoidales
- Page ID
- 85941
CA, o corriente alterna, se llama así porque la corriente alterna o voltea hacia adelante y hacia atrás entre dos polaridades. En otras palabras, la corriente (y consecuentemente la tensión) es una función del tiempo. Esto es fundamentalmente diferente de la corriente continua que es fija en polaridad y generalmente constante en el tiempo. Una fuente de voltaje de CC de laboratorio, por ejemplo, idealmente mantiene un voltaje establecido a través de sus terminales y no varía con el tiempo. Por el contrario, a medida que una forma de onda de CA oscila de un lado a otro a través del tiempo, su forma puede exhibir amplias variaciones que van desde los caminos simples y regulares de los estándares de laboratorio como las ondas sinusoidales, las ondas triangulares y las ondas cuadradas, hasta las formas de onda mucho más complejas y ondulantes producidas por los instrumentos musicales y el voz humana.
La onda sinusoidal es la onda más simple que se puede crear. Representa el movimiento de un simple vector que gira a una velocidad constante, como el desplazamiento vertical de la segunda manecilla de un reloj. Un ejemplo se muestra en la Figura\(\PageIndex{1}\). El eje horizontal traza el tiempo. Aumenta a medida que nos movemos de izquierda a derecha (es decir, si el punto A está a la derecha del punto B, entonces A ocurre más tarde en el tiempo que B). El eje vertical se representa aquí en general como un porcentaje del máximo pero normalmente sería una medición de voltaje, corriente, presión sonora, o similares.
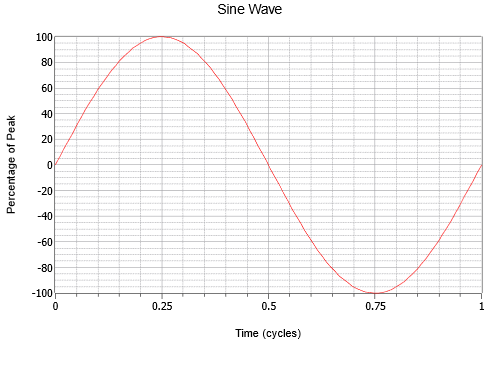
Observe la variación suave que comienza en cero, se eleva a un pico positivo en un cuarto de camino, vuelve a caer a cero cuando está a mitad de camino, continúa a un pico negativo a tres cuartos, y luego vuelve a subir a donde comenzó. Este proceso luego se repite. Cada repetición se conoce como un ciclo. En la Figura\(\PageIndex{1}\), se muestra un ciclo completo.
Las ondas sinusoidales exhiben simetría de un cuarto Es decir, cada cuarto (en el tiempo) de la ola es idéntico a cualquier otro si simplemente la volteas alrededor del eje horizontal y/o la giras erguida alrededor de su pico. El tiempo que se tarda en completar un ciclo se llama período y se denota con el símbolo\(T\) (para Tiempo). El recíproco del periodo es la frecuencia,\(f\).
\[f = \frac{1}{T} \label{1.1} \]
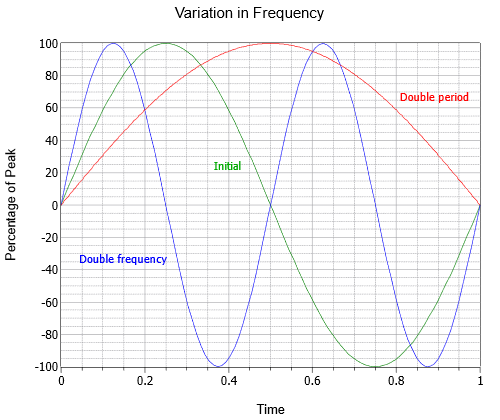
La frecuencia indica cuántos ciclos existen en un segundo. Para honrar a uno de los investigadores del siglo XIX en la materia, en lugar de llamar a la unidad “ciclos por segundo”, utilizamos Hertz, que lleva el nombre de Heinrich Hertz y abreviado Hz. En la Figura se muestran\(\PageIndex{2}\) tres ondas sinusoidales con diferentes frecuencias; la onda inicial (verde), una onda al doble de la frecuencia (azul), y una tercera a la mitad de la frecuencia o dos veces el periodo (rojo).
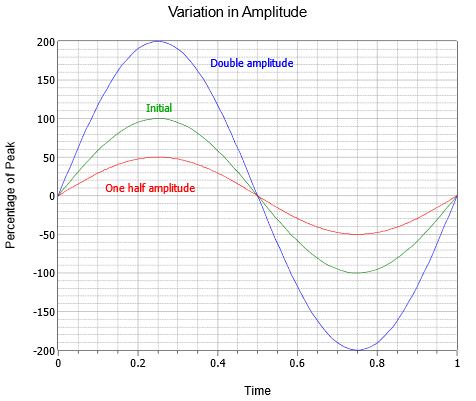
La amplitud (vertical) de la onda se puede expresar como una cantidad máxima, que es el cambio desde la línea de cero central hasta el valor más positivo. La amplitud también se puede expresar como pico a pico; la distancia de la más negativa a la más positiva. Para una onda sinusoidal esto siempre será el doble del valor pico, aunque ese podría no ser el caso de otras ondas que pueden ser asimétricas. En la Figura se muestra una serie de tres ondas sinusoidales con amplitudes diferentes\(\PageIndex{3}\). A lo largo de las versiones iniciales (verde) se encuentran las versiones de doble amplitud (azul) y media amplitud (roja).
Combinando estos parámetros, considere la forma de onda de voltaje mostrada en la Figura\(\PageIndex{4}\). Aquí vemos dos ciclos de una forma de onda de voltaje de CA.
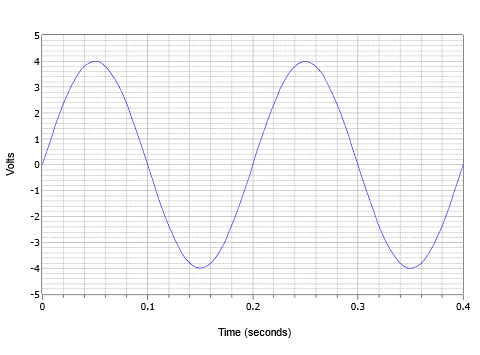
El valor pico es de 4 voltios y el valor de pico a pico es de 8 voltios (normalmente abreviado como “8 V pp”). El periodo de un ciclo es de 0.2 segundos, o\(T = 200\) milisegundos. Además, la frecuencia,\(f = 1/200\) milisegundos, o 5 Hz (5 ciclos en un segundo).
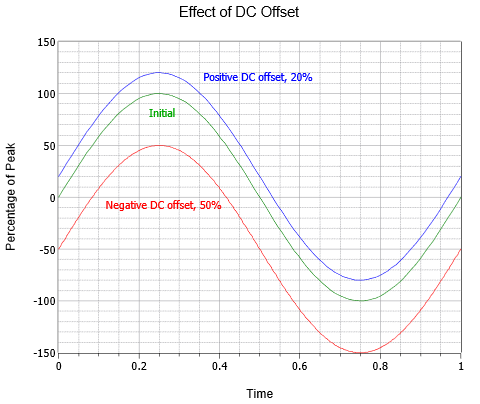
Las formas de onda de CA también se pueden combinar con un desplazamiento de CC. Agregar un nivel de CC positivo desplaza la onda hacia arriba verticalmente, mientras que un nivel de CC negativo desplaza la onda hacia abajo verticalmente. Esto no altera la frecuencia o porción de CA de la amplitud (aunque los picos absolutos se desplazarían por el valor de CC). La figura\(\PageIndex{5}\) muestra el efecto de varios desplazamientos de CC. Por encima de la onda inicial (verde) hay una onda por lo demás idéntica con un desplazamiento de CC positivo igual al 20% del valor máximo original (azul). Por debajo del original hay una tercera onda (roja) que exhibe un desplazamiento de CC negativo igual a la mitad del valor pico del original.
Además, es posible que una onda sinusoidal se desplace en el tiempo en comparación con alguna otra onda sinusoidal o referencia. Si bien es posible indicar este desplazamiento como un tiempo absoluto, es más común hacerlo como un desplazamiento de fase, es decir, el tiempo expresado como una porción del periodo en grados. Por ejemplo, si un seno está por delante de otro una cuarta parte del periodo, se dice que está liderando por 90\(^{\circ}\) (es decir, 1/4 de 360\(^{\circ}\)). Si está atrasado por ½ del periodo, se dice que está rezagado por 180\(^{\circ}\) (es decir, más tarde en el tiempo por 1/2 ciclo). Otra forma de afirmar esto es que las formas de onda principales comienzan más temprano en el tiempo y así se dibujan a la izquierda de la referencia, mientras que las formas de onda rezagadas comienzan más tarde en el tiempo y se dibujan hacia la derecha.
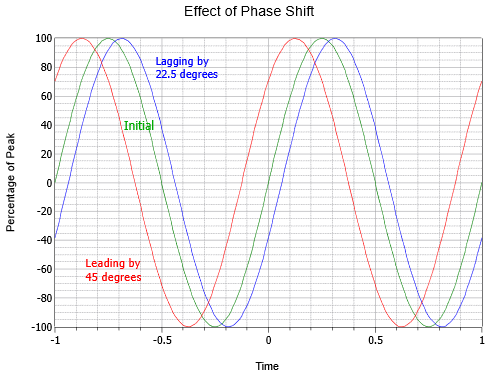
La figura\(\PageIndex{6}\) ilustra el efecto del desplazamiento de fase. Obsérvese que en esta parcela, se\(t = 0\) ha movido al centro del eje horizontal. La curva media es la onda inicial, o de referencia, (verde). A la izquierda (roja) hay una onda que conduce a la onda inicial en un octavo ciclo, o 45\(^{\circ}\). A la derecha (azul), hay una onda rezagada de la mitad, o −22.5\(^{\circ}\).
Combinar los elementos anteriores nos permite desarrollar un formato general para una onda sinusoidal (voltaje mostrado):
\[v(t) = V_{DC} + V_{P} \sin (2 \pi f t + \theta) \label{1.2} \]
donde
- \(v(t)\)es el voltaje en algún momento\(t\),
- \(V_{DC}\)es el desplazamiento de CC, si lo hay,
- \(V_{P}\)es el valor pico,
- \(f\)es la frecuencia,
- \(\theta\)es el desplazamiento de fase (+ si está dirigido y dibujado a la izquierda, − si está retrasado y dibujado a la derecha).
Para un ejemplo rápido y práctico, la forma de onda mostrada en la Figura\(\PageIndex{4}\) tiene una amplitud de pico de 4 voltios, una frecuencia de 5 Hz, y sin desplazamiento de CC o desplazamiento de fase. Así, su expresión es\(v(t) = 4 \sin (2 \pi 5 t)\)
Para calcular un desplazamiento de fase, primero determine el diferencial de tiempo entre la forma de onda y la referencia, a la que llamaremos\(\Delta t\). La referencia puede ser un punto fijo en el tiempo (por ejemplo\(t = 0\)) u otra forma de onda. Generalmente, la manera más fácil de hacer esto es medir la diferencia en los cruces por cero, asumiendo que no hay desplazamiento de CC. Si hay un desplazamiento, realice la medición donde se haya desplazado el cruce por cero (es decir, en el nivel de desplazamiento de CC). Una vez encontrada la diferencia, divídala por el periodo para representar el desplazamiento como fracción de un periodo. Como un ciclo representa una rotación del vector, o 360 grados, simplemente multiplique la fracción por 360 grados para encontrar el desplazamiento de fase en grados. Expresado como una fórmula:
\[\theta = 360^{\circ} \frac{\Delta t}{T} \label{1.3} \]
Recuerde, si la onda se desplaza hacia la izquierda entonces es delantera y positiva, mientras que un desplazamiento hacia la derecha está rezagado o retrasado en el tiempo, y por lo tanto negativo.
Ejemplo\(\PageIndex{1}\)
Escribe la expresión para la forma de onda que se muestra en la Figura\(\PageIndex{7}\).
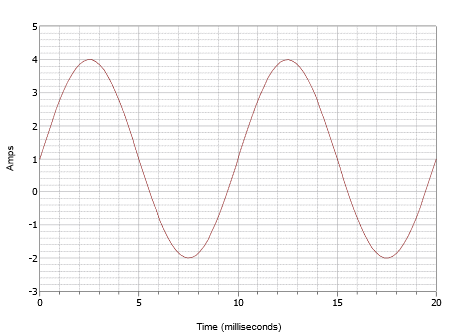
Esta forma de onda superficialmente puede parecerse a la de la Figura\(\PageIndex{4}\) pero no dejes que esto te engañe. En primer lugar, la escala de tiempo es diferente. Para esta forma de onda, un ciclo se completa en 10 milisegundos. Por lo tanto, la frecuencia es
\[\begin{align} f &= \frac{1}{T} \\[4pt] &= \frac{1}{10 ms} \\[4pt] &= 100 Hz \end{align} \nonumber \]
El segundo problema es el desplazamiento de CC. Tenga en cuenta que el pico positivo ocurre a 4 amperios mientras que el pico negativo ocurre a -2 amperios. Esto indica un valor pico a pico de 6 amperios. Sin un desplazamiento, el pico positivo estaría en 3 amperios, por lo tanto hay un desplazamiento de CC de +1 amperios. El centro vertical de la forma de onda se desplaza hacia arriba de 0 amperios a +1 amperios. Este punto está en t = 0, por lo tanto, no hay desplazamiento de fase. La expresión resultante es:
\[i(t) = 1 + 3 \sin (2 \pi 100 t) \nonumber \]
Ejemplo\(\PageIndex{2}\)
Escribe la expresión para la forma de onda que se muestra en la Figura\(\PageIndex{8}\).
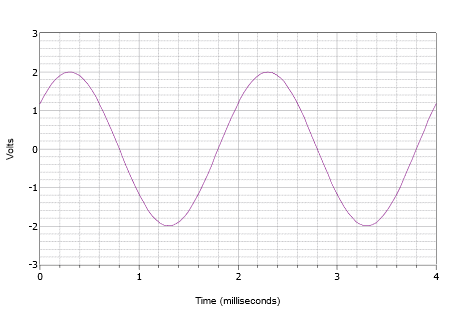
En primer lugar, el pico positivo es de 2 voltios y el valor de pico a pico es de 4 voltios. Por lo tanto, no hay compensación de CC. El centro vertical de la onda no inicia en\(t = 0\), por lo tanto, debe haber un desplazamiento de fase. El valor a\(t = 0\) es de 1.2 voltios. La onda golpea esta misma amplitud a\(t = 2\) milisegundos y comienza a repetir otro ciclo. En consecuencia el periodo debe ser de 2 milisegundos. La frecuencia es el recíproco de este valor, y por lo tanto\(f = 500\) Hz.
La forma de onda se desplaza hacia la izquierda, lo que indica un desplazamiento de fase positivo o inicial. Si examinamos el segundo ciclo, vemos que alcanza cero voltios a 1.8 milisegundos. Por lo tanto, el desplazamiento es de 0.2 milisegundos. Expresado en grados esto es:
\[\theta = 360^{\circ} \frac{\Delta t}{T} \nonumber \]
\[\theta = 360^{\circ} \frac{0.2ms}{2 ms} \nonumber \]
\[\theta = 36^{\circ} \nonumber \]
La expresión final es:
\[v(t) = 2 \sin (2 \pi 500 t + 36^{\circ}) \nonumber \]
Ejemplo\(\PageIndex{3}\)
Dibuja la forma de onda correspondiente a la siguiente expresión.
\[v(t) = −3 + 5 \sin (2 \pi 40000 t − 72^{\circ}) \nonumber \]
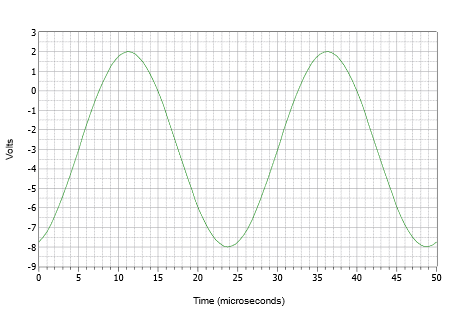
Primero, tenga en cuenta que el desplazamiento de -3 voltios empuja el pico positivo hacia abajo de 5 voltios a 2 voltios, y el pico negativo hacia abajo de −5 voltios a −8 voltios. La frecuencia de 40 kHz dicta un periodo de:
\[\begin{align*} T &= \frac{1}{f} \\[4pt] &= \frac{1}{40 kHz} \\[4pt] &= 25 \mu s \end{align*} \nonumber \]
El desplazamiento de fase de −72\(^{\circ}\) representa 72/360, o 0.2 ciclos. Esto corresponde a un retardo de tiempo (desplazado a la derecha porque es negativo) de 0.2 veces 25\(\mu\) s, o 5\(\mu\) s.
Inicialmente, a menudo es mejor construir la trama a través de una serie de pasos discretos en lugar de tratar de dibujar todo de una sola vez. Primero, dibuje una onda sinusoidal con una amplitud pico de 5 voltios y un período de 25\(\mu\) s. Ahora, empuje la forma de onda hacia abajo 3 voltios para que el pico positivo sea de solo 2 voltios y el pico negativo esté abajo en −8 voltios. Finalmente, empuje la forma de onda recién desplazada hacia la derecha 5\(\mu\) s. El resultado se muestra en la Figura\(\PageIndex{9}\).
Mediciones de Laboratorio
En el laboratorio, se utiliza un generador de funciones para generar senos y otras formas de onda. Estos dispositivos permitirán un control preciso tanto sobre la amplitud como la frecuencia de la onda junto con la adición de un desplazamiento de CC, si se desea. Un ejemplo se muestra en la Figura\(\PageIndex{10}\). La herramienta de medición correspondiente es el osciloscopio, o simplemente el alcance, para abreviar.

El osciloscopio es quizás el dispositivo de medición más útil y versátil del laboratorio. Por lo general, cuentan con dos o cuatro canales de entrada, aunque son posibles más. Cada canal de entrada tiene su propio ajuste de sensibilidad y todos los canales comparten una referencia de tiempo común. La pantalla dibuja formas de onda de la misma manera que las que se ven en las Figuras\(\PageIndex{1}\) —\(\PageIndex{9}\). Además, pueden trazar una tensión frente a otra (modo X — Y). Los osciloscopios modernos tienen características adicionales como la medición automática de frecuencia, amplitud, desplazamiento de fase, etc., mediciones basadas en cursores y la capacidad de guardar imágenes de visualización como archivos gráficos. Un ejemplo de un osciloscopio digital de cuatro canales se muestra en la Figura\(\PageIndex{11}\).

Símbolos esquemáticos
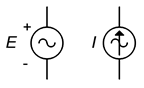
En lo que respecta a los esquemas, los símbolos para las fuentes de voltaje y corriente alterna se muestran en la Figura\(\PageIndex{12}\). Las marcas de polaridad y dirección no son absolutas; después de todo, se trata de fuentes de CA cuya polaridad y direcciones giran hacia adelante y hacia atrás. Los marcadores se utilizan en cambio para establecer una referencia de temporización, especialmente en circuitos que emplean múltiples fuentes.
Vale la pena recordar que negar una fuente es lo mismo que voltear su polaridad. Esto fue cierto para las fuentes de CC y sigue siendo cierto para las fuentes de CA. Esto se ilustra en la Figura\(\PageIndex{13}\). En ocasiones, voltear o negar la fuente hará que el análisis sea un poco más obvio o más fácil de visualizar.
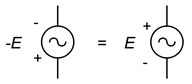
Ejemplo\(\PageIndex{4}\)
Supongamos que un osciloscopio muestra dos ondas como se representa en la Figura\(\PageIndex{14}\). Determine el desplazamiento de fase de la forma de onda de pico de 20 voltios (azul) más pequeña en relación con la forma de onda de pico (rojo) de 25 voltios
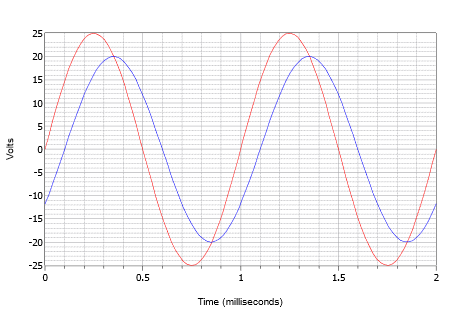
Primero, tenga en cuenta que ninguna de las ondas presenta un desplazamiento de CC. Si uno o ambos tuvieran un desplazamiento, la (s) onda (s) tendría que desplazarse verticalmente para que sus puntos normales de cruce por cero estuvieran en el mismo nivel. Al medir cualquiera de las ondas, se encuentra que el periodo es de 1 milisegundo. El cambio de tiempo se puede encontrar más fácilmente en cualquiera de los cruces por cero (hay cuatro ubicaciones para elegir). El retraso es una pequeña desviación, o 0.1 milisegundos, con la onda más pequeña retrasada en el tiempo, o retrasando la onda más grande. Esto indica un desplazamiento de fase negativo.
\[\theta = 360^{\circ} \frac{\Delta t}{T} \nonumber \]
\[\theta = 360^{\circ} \frac{−0.1 ms}{1 ms} \nonumber \]
\[\theta = −36^{\circ} \nonumber \]
Senos y Cosinos
Hay un puñado de cambios de fase específicos que merecen una mirada más cercana. Si se invierte una onda sinusoidal, es decir, volteada boca abajo, es indistinguible de una onda sinusoidal que ha sido desplazada ya sea +180 o −180 grados. En otras palabras, tal onda se puede escribir de tres maneras diferentes:\(− \sin (2 \pi ft)\),\(\sin (2 \pi ft − 180^{\circ})\), o\(\sin (2 \pi ft + 180^{\circ})\). Además, si una onda sinusoidal se desplaza +90 grados (es decir, delantera y hacia la izquierda), también puede denominarse onda coseno. Por lo tanto\(\sin (2 \pi ft + 90^{\circ}) = \ cos (2 \pi ft)\). Finalmente, si una onda sinusoidal se desplaza en −90 grados (es decir, retrasada y hacia la derecha), puede denominarse onda coseno negativa o invertida. Por lo tanto\(\sin (2 \pi ft − 90^{\circ}) = − \cos (2 \pi ft)\). Las relaciones de estas cuatro ondas se ilustran en la Figura\(\PageIndex{15}\).
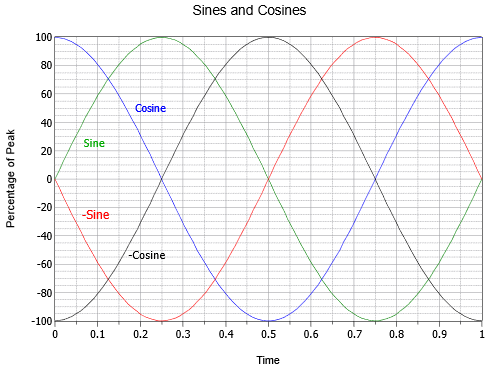
También vale la pena señalar que la onda coseno representa la primera derivada, o pendiente, de la onda sinusoidal. Como recordarás de otros estudios, la pendiente o “pendiente” de una línea es la relación entre el cambio vertical y el cambio horizontal, a veces llamado “el ascenso sobre la carrera”. Para un voltaje, sería el cambio de voltaje sobre el cambio en el tiempo, o\(\Delta V/ \Delta t\). Para una curva suave y continuamente cambiante como una onda sinusoidal, la pendiente en un punto dado se define correctamente como la primera derivada, o\(dv/dt\) en este caso. Para verificar que esto sea cierto visualmente, tenga en cuenta que la parte más empinada de la onda sinusoidal (verde) es donde cruza la amplitud cero. Al cruzar cero mientras se mueve positivo (en\(t = 0\) o\(t = 1\) en la Figura\(\PageIndex{15}\)), el coseno (azul) se encuentra en su pico positivo. A medida que el seno cruza cero mientras se mueve negativo (at\(t = 0.5\)), el coseno está en su pico negativo. Además, la onda sinusoidal es plana con una pendiente de cero en sus picos positivos y negativos (at\(t = 0.25\) y\(t = 0.75\), respectivamente), y en esos momentos la amplitud del coseno también es cero. También es cierto que la onda sinusoidal es la pendiente de la onda coseno negativa, el coseno negativo es la pendiente del seno negativo, y el seno negativo es la pendiente del coseno. Moviéndose en sentido inverso, podemos decir que la anti-derivada (integral indefinida) de una onda coseno es una onda sinusoidal, la integral de una onda sinusoidal es una onda coseno negativa, y así sucesivamente. Estas relaciones resultarán más útiles cuando dirigimos nuestra atención a la respuesta de capacitores e inductores en circuitos de CA.
— Medición cuadrática media de raíz
Junto con pico y pico a pico, la amplitud se puede dar como un valor RMS (raíz cuadrática media). De hecho, si no se especifica pico o pico a pico, se supone que la medición es RMS. RMS es un cálculo especial que se utiliza para encontrar una potencia de CC equivalente (muy común, por ejemplo, con amplificadores de potencia de audio). Es decir, si estamos interesados en encontrar la potencia en una resistencia, el cálculo debe realizarse utilizando valores RMS para voltaje o corriente, no valores pico o pico a pico. De no hacerlo, se traducirán en poderes erróneos. Esto es cierto independientemente de la forma de onda; ya sea una onda sinusoidal, una onda triangular o las ondas complejas de las señales musicales. Si se especifica un voltaje como RMS, se puede tratar para cálculos de potencia como un voltaje de CC de tamaño equivalente. Por ejemplo, un seno RMS de 1 voltio producirá la misma disipación de potencia y calentamiento en una resistencia dada que lo hará 1 voltio CC. Por esta razón, RMS se denomina a veces el valor efectivo (es decir, valor efectivo de CC).
El nombre raíz-medio-cuadrado describe el proceso de determinación del valor efectivo. Primero, recordemos que la potencia es proporcional al cuadrado de la tensión o corriente. Así, nuestro primer paso será cuadrar la forma de onda de entrada. Por supuesto, la forma de onda es función del tiempo y su cuadrado dará alguna nueva forma. En este punto, necesitamos encontrar el valor promedio de esta nueva forma. La razón de esto es simple, pero no necesariamente obvia. Los componentes eléctricos y electrónicos tienen masa, y por lo tanto no se calientan ni se enfrían instantáneamente. Exhiben una constante térmica de tiempo. Por lo tanto, responden al ingreso promedio a lo largo del tiempo. Si bien podríamos calcular alguna forma de “potencia pico instantánea” en algún instante específico en el tiempo, no representa la potencia de CC equivalente. Una vez que hemos obtenido el valor medio de esta forma de onda cuadrada, el valor DC correspondiente es solo la raíz cuadrada de la media. El resultado es un valor fraccional entre cero y uno que se utiliza como factor de escala para convertir un valor pico en un valor RMS. El valor será único para la forma de onda específica. Es decir, todos los senos (independientemente de la fase) tienen el mismo factor, todas las ondas triangulares regulares tienen el mismo factor, y así sucesivamente. Como nos preocupamos principalmente por los senos, echemos un vistazo más de cerca a determinar el factor RMS para ellos.
Comenzamos con la expresión básica para una onda sinusoidal sin desplazamiento de CC o desplazamiento de fase, y con una amplitud de uno:
\[v(t) = \sin (2 \pi f t) \nonumber \]
El primer paso es cuadrar esta forma de onda. Una identidad trigonométrica útil es
\[( \sin x)^2 = \frac{1}{2} − \frac{1}{2} \cos 2 x \nonumber \]
Aplicando esto a nuestros rendimientos de onda:
\[v(t)^2 = \frac{1}{2} − \frac{1}{2} \cos (2 \pi 2 f t) \nonumber \]
Esta expresión describe una onda coseno invertida al doble de la frecuencia original y la mitad de la amplitud original, montando sobre un desplazamiento de CC igual a su valor máximo. En otras palabras, el pico negativo del coseno está en cero y el pico positivo está en 1. El siguiente paso es encontrar el valor promedio o medio de este resultado intermedio. La media es igual al desplazamiento de 0.5. Esto se puede visualizar como el área por encima del desplazamiento llenando perfectamente la “inmersión” debajo del desplazamiento. El paso final es tomar la raíz cuadrada de la media. La raíz cuadrada de 0.5 es igual a una sobre la raíz cuadrada de dos, o aproximadamente 0.707. Por lo tanto, el valor RMS es 0.707 veces el pico. Como alternativa, se podría dividir el pico por raíz cuadrada de dos, o aproximadamente 1.414. Este proceso se muestra gráficamente en la Figura\(\PageIndex{16}\).
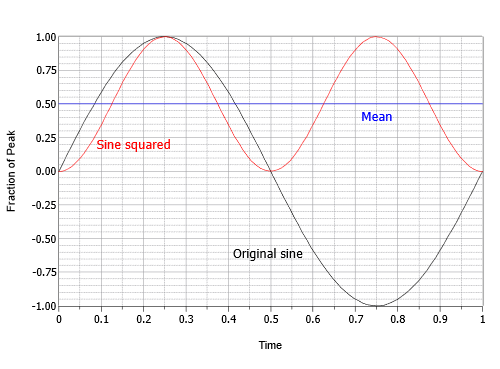
En suma, para las ondas sinusoidales, RMS es siempre el valor pico por 0.707. También podríamos decir que el valor RMS de cualquier onda sinusoidal es su pico dividido por aproximadamente 1.414. Nuevamente, estas relaciones no serían necesariamente ciertas para las ondas no sinusoidales. Los detalles sobre otras formas comunes se pueden encontrar en el Apéndice C. Finalmente, la relación entre el valor pico y el valor RMS se denomina relación de cresta. Este es un valor fijo para las ondas sinusoidales (nuevamente, alrededor de 1.414), pero puede ser superior a 10:1 para algunos tipos de señales de audio.
Longitud de onda
Otro elemento de interés es la velocidad de propagación de la ola. Esto varía ampliamente. En el caso de la luz en un vacío (o a una aproximación cercana, una corriente eléctrica en un cable), la velocidad es de aproximadamente 3E8 metros por segundo (es decir, 300,000 km/s) o aproximadamente 186,000 millas por segundo.
Dada una velocidad y un periodo, podemos imaginar cuán separados están los picos de la ola. Esta distancia se llama la longitud de onda y se denota con la letra griega lambda\(\lambda\). La longitud de onda es igual a la velocidad dividida por la frecuencia,\(\lambda = v/f\). Así, para un altavoz que produce un seno de 100 Hz, ya que la velocidad del sonido en el aire es de 344 m/s, luego\(\lambda = 344 m/s \, / \, 100\) Hz, o 3.44 metros (un poco más de 11 pies). Observe que cuanto mayor sea la frecuencia, más corta es la longitud de onda. Además, tenga en cuenta que cuanto más rápida sea la velocidad, mayor será la longitud de onda. Los cálculos de longitud de onda son de particular importancia en los campos de las telecomunicaciones y la acústica.


