1.3: Análisis Básico de Fourier
- Page ID
- 85949
El teorema de Fourier, llamado así por el matemático francés Jean-Baptiste Joseph Fourier, afirma que cualquier forma de onda repetitiva puede representarse como una colección de ondas sinusoidales y cosenales de la amplitud y frecuencia adecuadas. Como alternativa, puede representarse como una serie de ondas sinusoidales cada una con la amplitud, frecuencia y fase adecuadas. Esto incluye señales complejas como la voz humana y los instrumentos musicales. En consecuencia, si un sistema es lineal, la respuesta de un sistema a una onda compleja puede entenderse en términos de su respuesta a las ondas sinusoidales individuales, vía superposición.
En esta colección de ondas, cada componente es conocido como un parcial con el componente de menor frecuencia conocido como el fundamental. Todos los demás parciales se agrupan y se denominan armónicos. Las formas de onda “regulares” como las ondas cuadradas y las ondas triangulares presentan una secuencia armónica armónica, lo que significa que estos armónicos son múltiplos enteros de lo fundamental. Como atajo, a menudo se les conoce como solo armónicos.
Puede ser difícil de visualizar inicialmente, pero como todas las ondas, las ondas en forma de cuadrado o triángulo están formadas por una serie de senos. La ecuación para una onda cuadrada es:
\[v(t) = \sum_{n=1}^{\infty} \frac{1}{2n-1} \sin ((2n-1)2 \pi ft) \label{1.4} \]
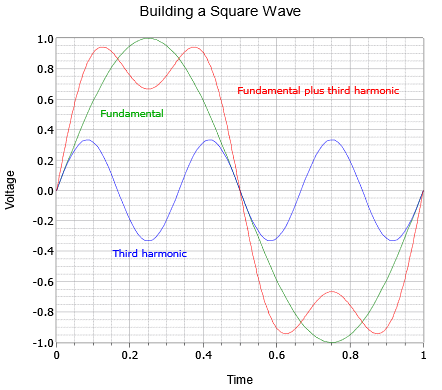
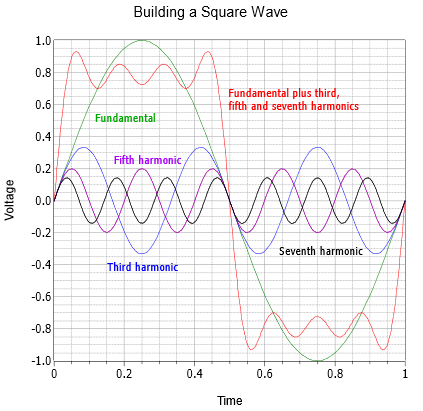
Esto dice que una onda cuadrada de frecuencia\(f\) se compone de una serie infinita de senos en múltiplos enteros impares de\(f\), con una característica de amplitud inversa. Por ejemplo, un cuadrado de 100 Hz consiste en un seno de 100 Hz, más un seno de 300 Hz a 1/3 de amplitud, más un seno de 500 Hz a 1/5 de amplitud, más un seno de 700 Hz a 1/7 de amplitud, y así sucesivamente.
Una onda triangular es similar:
\[v(t) = \sum_{n=1}^{\infty} \frac{1}{(2n-1)^2} \cos ((2n-1)2 \pi ft) \label{1.5} \]
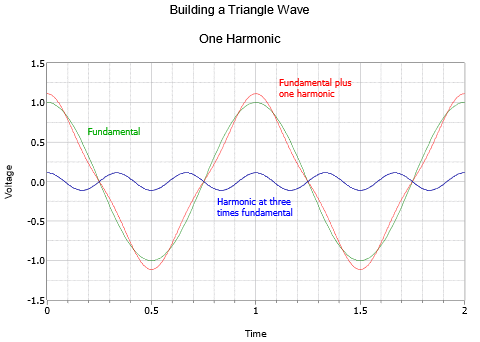
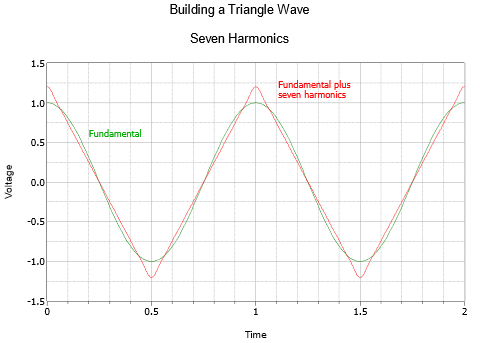
Así, una onda triangular de frecuencia\(f\) se compone de una serie infinita de cosenos (senos con un desplazamiento de fase de 90 grados o un cuarto de ciclo) a múltiplos enteros impares de\(f\), con una característica de amplitud cuadrada inversa. Por ejemplo, un triángulo de 100 Hz consiste en un coseno de 100 Hz, más un coseno de 300 Hz a 1/9 de amplitud, más un coseno de 500 Hz a 1/25 de amplitud, más un coseno de 700 Hz a 1/49 de amplitud, y así sucesivamente.
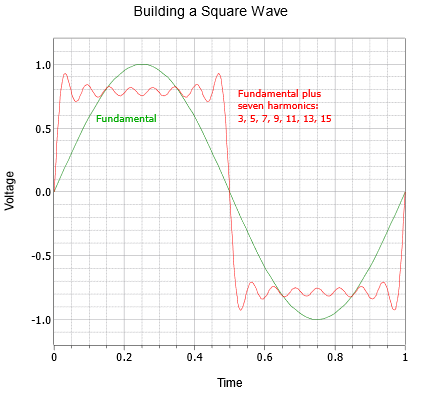
Sigue una serie de gráficas que muestran la construcción de una onda cuadrada y una onda triangular. La secuencia de onda cuadrada comienza con lo fundamental y el primer armónico en la Figura\(\PageIndex{1}\). El resultado es una onda extrañamente llena de baches. La segunda gráfica de la Figura\(\PageIndex{2}\) suma los dos armónicos siguientes. A medida que se agregan más armónicos, los lados se vuelven más pronunciados y la parte superior/inferior comienzan a aplanarse. Se aplanan porque cada armónico adicional cancela parcialmente algunos de los picos y valles de la suma anterior. Esto da lugar a un mayor número de ondulaciones siendo cada ondulación menor en amplitud. La secuencia termina con la Figura\(\PageIndex{3}\) que muestra siete armónicos que se agregan con el resultado acercándose a una onda cuadrada razonable. A medida que se agregan cada vez más armónicos, la onda se acercaría a una parte superior e inferior plana con lados verticales, la onda cuadrada idealizada.
La secuencia triangular comienza con un fundamental y el primer armónico como se muestra en la Figura\(\PageIndex{4}\). La combinación resultante ya está alejándose de una simple forma sinusoidal. La segunda y última gráfica, Figura\(\PageIndex{5}\), muestra un total de siete armónicos. El resultado es muy cercano a un triángulo, la única desviación obvia es el ligero redondeo en los mismos picos. La adición de más armónicos haría que estos se agudizaran aún más.