Saltar al contenido principal
LibreTexts Español

8.5: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    85904

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

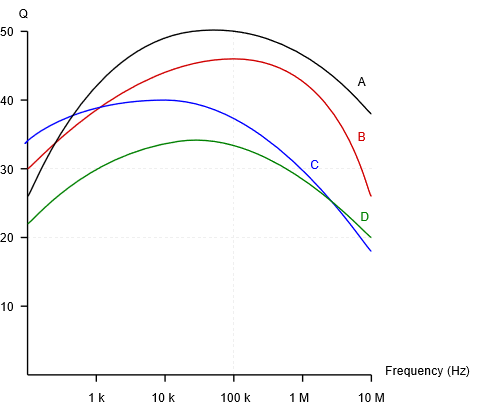
    clipboard_eb02aaa3d3d4549b2ea1e6c749b9cb4c2.png

    \(Q\)Curvas inductoras para ser utilizadas con los ejercicios a continuación

    Análisis

    1. Un circuito tiene una frecuencia resonante de 440 kHz y un sistema\(Q\) de 30. Determinar el ancho de banda y los valores aproximados para\(f_1\) y\(f_2\).

    2. Un circuito tiene una frecuencia resonante de 19 kHz y un ancho de banda de 500 Hz. Determinar el sistema\(Q\) y los valores aproximados para\(f_1\) y\(f_2\).

    3. Encuentre la resistencia\(Q_{coil}\) y la bobina de un inductor de 150\(\mu\) H a 100 kHz usando la curva A del dispositivo.

    4. Encuentre la resistencia\(Q_{coil}\) y la bobina de un inductor de 2.2 mH a 50 kHz usando la curva D del dispositivo.

    5. A cierta frecuencia, la impedancia de un inductor es\(24 + j600\)\(\Omega\). Determinar la resistencia paralela y la reactancia que produce el mismo valor.

    6. A cierta frecuencia, la impedancia de un inductor es\(3 + j150\)\(\Omega\). Determinar la resistencia paralela y la reactancia que produce el mismo valor.

    7. Un cierto inductor de 75\(\mu\) H se describe por la curva B. Determinar la combinación equivalente de inductor/resistencia paralelo a 1 MHz.

    8. Un cierto inductor de 3.3 mH se describe por la curva C. Determine la combinación equivalente de inductor/resistencia paralelo a 20 kHz.

    9. Considere un circuito en serie que consta de un condensador de 2 nF, un inductor ideal de 33\(\mu\) H y una\(\Omega\) resistencia de 5. Determine la frecuencia resonante, el sistema y\(Q\) el ancho de banda.

    10. Considere un circuito en serie que consta de un condensador de 20 nF, un inductor ideal de 100\(\mu\) H y una\(\Omega\) resistencia de 2.7. Determine la frecuencia resonante, el sistema y\(Q\) el ancho de banda.

    11. Considera un circuito en serie que consta de un condensador de 50 nF, un inductor de 20 mH con\(Q_{coil}\) de 50 y una\(\Omega\) resistencia 63. Determine la frecuencia resonante, el sistema y\(Q\) el ancho de banda.

    12. Considere un circuito en serie que consiste en un condensador de 200 nF, un inductor\(Q_{coil}\) de 1 mH con 65 y una\(\Omega\) resistencia 72. Determine la frecuencia resonante, el sistema y\(Q\) el ancho de banda.

    13. Para el circuito que se muestra en la Figura\(\PageIndex{1}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Asumir\(R_{coil} = 0\)\(\Omega\). Si la fuente es de pico de 1 voltio, determine el voltaje del condensador en resonancia.

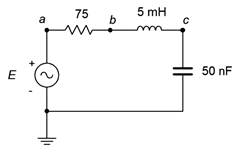
    clipboard_e6ea3b61eee3e2aeafabfeb6c78f05aef.png

    Figura\(\PageIndex{1}\)

    14. Para el circuito que se muestra en la Figura\(\PageIndex{2}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Asumir\(R_{coil} = 0\)\(\Omega\). Si la fuente es de 10 voltios, determine el voltaje del condensador en resonancia.

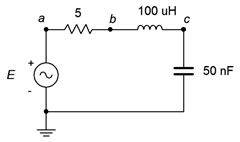
    clipboard_efd2aa3ea8c372d7e228b7d531ade26b6.png

    Figura\(\PageIndex{2}\)

    15. Repite el problema 13 pero asumamos en su lugar que el inductor es\(R_{coil} = 15\)\(\Omega\).

    16. Repita el problema 12 pero supongamos en su lugar que el inductor sigue la curva D.

    17. Para el circuito que se muestra en la Figura\(\PageIndex{3}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Si la fuente es de pico de 20 mA, determine los voltajes de resistencia y condensador en resonancia.

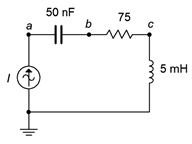
    clipboard_eea748d064b722fe17022e771437346e4.png

    Figura\(\PageIndex{3}\)

    18. Para el circuito que se muestra en la Figura\(\PageIndex{4}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Si la fuente es de 100 mA, determine los voltajes de resistencia y condensador en resonancia.

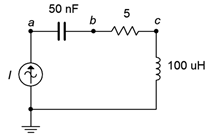
    clipboard_e9e2777f5ff6affe65628a2057c4f62fa.png

    Figura\(\PageIndex{4}\)

    19. Para el circuito que se muestra en la Figura\(\PageIndex{5}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Si la fuente es de 15 voltios, determine las corrientes del inductor y del condensador en resonancia. Supongamos que la resistencia de la bobina del inductor es 3.2\(\Omega\).

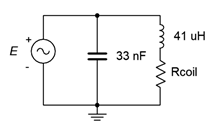
    clipboard_e228bba72feb212bad92822d329b3bcfc.png

    Figura\(\PageIndex{5}\)

    20. Para el circuito que se muestra en la Figura\(\PageIndex{6}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Si la fuente es de 3 voltios, determine las corrientes del inductor y del condensador en resonancia. Supongamos que los inductores\(Q\) son 30.

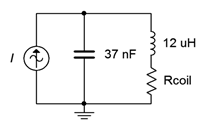
    clipboard_e04f7ab96a8909cb60cb7a796d27f725b.png

    Figura\(\PageIndex{6}\)

    21. Para el circuito que se muestra en la Figura\(\PageIndex{7}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Si la fuente es de 15 voltios, determine las corrientes de resistencia, inductor y condensador en resonancia.

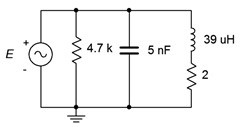
    clipboard_eb47d859996533e0c0a254eb35195c645.png

    Figura\(\PageIndex{7}\)

    22. Dado el circuito mostrado en la Figura\(\PageIndex{8}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Si la fuente es de 2 voltios, determine las corrientes de resistencia, inductor y condensador en resonancia. Supongamos que la resistencia de la bobina del inductor es 2.5\(\Omega\).

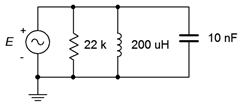
    clipboard_ebf7c4888324acf5d28741d1cca3a419c.png

    Figura\(\PageIndex{8}\)

    23. Para el circuito que se muestra en la Figura\(\PageIndex{9}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Si la fuente es de 5 voltios, determine las corrientes de resistencia, inductor y condensador en resonancia. Supongamos que el inductor\(Q\) es 40.

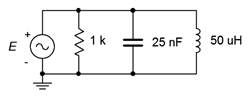
    clipboard_e9333f5345a5e752da56d1d834f0b7f4e.png

    Figura\(\PageIndex{9}\)

    24. Dado el circuito mostrado en la Figura\(\PageIndex{10}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Si la fuente es de 2.5 mA, determine el voltaje de la resistencia y las tres corrientes de derivación en resonancia.

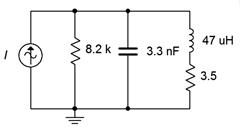
    clipboard_eeae051139cdc6bf56faf16b8c2285f44.png

    Figura\(\PageIndex{10}\)

    25. Para el circuito que se muestra en la Figura\(\PageIndex{11}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Si la fuente es de 500\(\mu\) A, determine el voltaje de la resistencia y las tres corrientes de derivación en resonancia. Supongamos que los inductores están dados por la curva C.\(Q\)

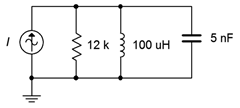
    clipboard_e6bf40b57f5fcce593710b4b8d8e09c14.png

    Figura\(\PageIndex{11}\)

    26. Dado el circuito mostrado en la Figura\(\PageIndex{12}\), determinar la frecuencia resonante, el sistema\(Q\) y el ancho de banda. Si la fuente es de 10 mA, determine el voltaje de la resistencia y las tres corrientes de derivación en resonancia. Supongamos que los inductores están dados por la curva B.\(Q\)

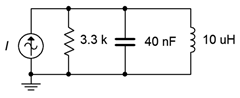
    clipboard_e3e71ef0e871616b9af99830b1c31ba96.png

    Figura\(\PageIndex{12}\)

    Diseño

    27. Un circuito resonante en serie tiene un requerido\(f_0\) de 50 kHz. Si se utiliza un condensador de 75 nF, determine la inductancia requerida.

    28. Un circuito resonante en serie tiene un requerido\(f_0\) de 210 kHz. Si se utiliza un inductor de 22\(\mu\) H, determine la capacitancia requerida.

    29. Un circuito resonante paralelo consiste en un condensador de 12 nF y un inductor de 27\(\mu\) H con un\(Q_{coil}\) de 55. Determinar la resistencia paralela adicional requerida para lograr un sistema\(Q\) de 40.

    30. Un circuito resonante en serie tiene un objetivo de diseño de\(f_0=200\) kHz con un ancho de banda de 5 kHz. ¿Cuáles de las curvas inductoras anteriores (A, B, C, D) representan posibles candidatos, si los hay, y por qué no?

    31. Un circuito resonante paralelo tiene un objetivo de diseño de\(f_0=1\) MHz con un ancho de banda de 20 kHz. ¿Cuáles de las curvas inductoras anteriores (A, B, C, D) representan posibles candidatos, si los hay, y por qué no?

    Desafío

    32. Un circuito resonante paralelo tiene un requerido\(f_0\) de 50 kHz y un ancho de banda de 4 kHz. Si se utiliza un condensador de 75 nF y la impedancia de carga es de 100 k\(\Omega\), determinar la inductancia requerida y mínima aceptable\(Q_{coil}\).

    33. Un circuito resonante paralelo consiste en un condensador de 150 nF y un inductor de 200\(\mu\) H que tiene una resistencia de bobina de 1\(\Omega\). El ancho de banda deseado para la red es de 2 kHz. Determinar el valor de resistencia a colocar en paralelo con la red para lograr este objetivo.

    34. Un circuito resonante consiste en un condensador de 4 nF en paralelo con una bobina de 100\(\mu\) H que tiene una resistencia de bobina de 5\(\Omega\). Determinar la frecuencia resonante y el ancho de banda. Además, supongamos que este circuito está cargado ahora por un amplificador que tiene una impedancia de entrada equivalente a 10 k\(\Omega\) resistiva en paralelo con 500 pF de capacitancia de entrada. Además, el amplificador está conectado a través de 25 pies de cable coaxial que exhibe una capacitancia de 33 pF por pie. Determine los cambios en la frecuencia resonante y el ancho de banda, si los hubiera, con esta carga.

    Simulación

    35. Utilizar un análisis de dominio de frecuencia AC para verificar los resultados del problema 13. Trazar el voltaje de la resistencia de 0.1\(f_0\) a 10\(f_0\).

    36. Utilizar un análisis de dominio de frecuencia AC para verificar los resultados del problema 19. Haga esto superponiendo gráficos de los voltajes de resistencia, condensador e inductor en un rango de 0.1\(f_0\) a 10\(f_0\).

    37. Investigar los efectos del inductor\(Q\) en el ancho de banda del sistema del problema 21. Trazar el voltaje del sistema de 0.01\(f_0\) a 100\(f_0\) tres veces, el primero usando la resistencia de bobina especificada y luego usando valores diez veces más grandes y diez veces más pequeños.

    38. Investigar los efectos de la tolerancia de componentes en la respuesta de frecuencia del sistema del problema 21. Trazar el voltaje del sistema de 0.1\(f_0\) a 10\(f_0\) usando una variación de Monte Carlo en la respuesta del dominio de frecuencia de CA. Establezca una tolerancia del 10% en el condensador, inductor y resistencia, pero no altere la resistencia de la bobina.

    39. Utilizar un análisis de dominio de frecuencia AC para verificar el diseño del problema 27. Trazar el voltaje de la resistencia de 0.1\(f_0\) a 10\(f_0\).

    40. Utilizar un análisis de dominio de frecuencia AC para verificar el diseño del problema 29. Trazar el voltaje del sistema de 0.1\(f_0\) a 10\(f_0\).

    41. A\(Q\) valores altos (>10) los voltajes del condensador y del inductor de los circuitos resonantes en serie tenderán a alcanzar el máximo muy cerca de la frecuencia resonante. A menor\(Q\) s, estos picos tienden a divergir. Una situación similar ocurre con las corrientes en circuitos resonantes paralelos. Investigar este efecto realizando un análisis de dominio de frecuencia AC sobre el problema 14. Gráficas superpuestas de\(v_{ab}\),\(v_{bc}\) y\(v_c\) para valores sucesivamente mayores de resistencia.

    42. Investigar el “\(Q\)aumento” de las corrientes reactivas en comparación con las corrientes fuente y resistivas en un circuito resonante paralelo. Una forma sencilla de verificar esto es colocando amperímetros de CA en cada una de las ramas del circuito que se muestra en la Figura\(\PageIndex{13}\). Uso\(R\) = 630\(\Omega\),\(C\) = 40 nF,\(L\) = 10\(\mu\) H y\(i\) = 1 mA. Vale la pena comparar conjuntos de simulaciones para diferentes valores de resistencia para ver los cambios de corriente en relación con el sistema\(Q\). Es posible que se requieran ligeras variaciones de la frecuencia de la fuente para alcanzar el pico.

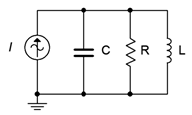
    clipboard_e5dab405b17f5a6f0adeef1942a00a1b6.png

    Figura\(\PageIndex{13}\)

    This page titled 8.5: Ejercicios is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by James M. Fiore via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.