1.4: Materiales dopados
- Page ID
- 83444
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Por sí mismos, los semiconductores intrínsecos no son de particular uso. No son buenos conductores ni aislantes, y su conducción depende en gran medida de la temperatura. Podemos alterar las propiedades del material introduciendo sustancias extrañas o impurezas en el cristal. Estas impurezas también se conocen como dopantes. Un cristal con un dopante agregado se conoce como un semiconductor extrínseco o material dopado. La cantidad de impureza añadida es generalmente pequeña, quizás en el barrio de una parte por millón. El dopante se puede agregar a través de un proceso de difusión gaseosa donde el cristal se calienta en un horno y el dopante se agrega en forma gaseosa. A lo largo de un periodo de tiempo las impurezas se difundirán o “filtrarán” en el cristal objetivo. Un enfoque alternativo es la implantación de iones. En este método las impurezas se aceleran y literalmente chocan en el blanco, desalojando y reemplazando algunos de los átomos originales en el cristal.
Hay dos tipos diferentes de semiconductores posibles. Uno se llama material de tipo N y el otro, material de tipo P. Como era de esperar, la N significa Negativo y la P significa (lo adivinaste) Positivo. El material tipo N se crea añadiendo impurezas pentavalentes, es decir, un dopante con cinco electrones en su capa externa. Los ejemplos incluyen fósforo, arsénico y antimonio. En contraste, el material tipo P se crea añadiendo una impureza trivalente, una con tres electrones en su capa externa. Posibles impurezas trivalentes incluyen boro, galio e indio.
1.4.1: Material Tipo N
La figura\(\PageIndex{1}\) muestra un modelo de un cristal de silicio con una impureza pentavalente en su centro. En comparación con un átomo de silicio ordinario que tendría cuatro electrones en su capa externa, la impureza pentavalente crea un electrón extra, o donante,. Por lo tanto, el cristal tiene una carga negativa neta y se le conoce como material de tipo N. El nivel de energía de los electrones donantes está justo por debajo de la parte inferior de la banda de conducción. En otras palabras, la diferencia entre el nivel donante y la parte inferior de la banda de conducción es mucho, mucho menor que la propia banda gap. Por lo tanto, es relativamente fácil para estos electrones donantes saltar a la banda de conducción, convirtiéndose en electrones ionizados libres y dejando atrás agujeros ionizados 1.
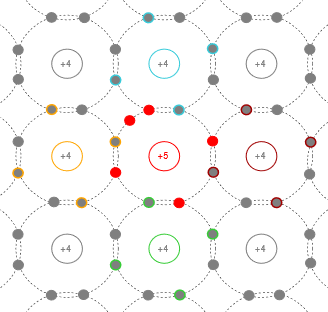
Figura\(\PageIndex{1}\): Cristal con impureza pentavalente añadida (tipo N).
Comparado con el cristal intrínseco no dopado, el cristal extrínseco dopado exhibe un número relativamente alto de electrones libres. Como puede suponer, esto mejora la conductividad del material, y cuanto mayor sea el nivel de dopaje, mayor será la mejora. Anteriormente se mencionó que tanto los electrones como los agujeros pueden servir como portadores de carga. Debido a que el número de electrones libres es significativamente mayor que el número de agujeros en el material de tipo N, los electrones en el material de tipo N se denominan el portador de carga mayoritario (o más simplemente, el portador mayoritario) mientras que los agujeros se denominan el portador de carga minoritaria (o portador minoritario).
Los electrones adicionales se suman al número de estados energéticos llenos y, al ser de mayor energía que los electrones de valencia, empujan el nivel de Fermi a un valor superior. Recuerde, el nivel Fermi representa el punto donde se llenaría el 50% de los estados, por lo que si sumamos estados por encima de este, entonces el nuevo punto del 50% debe ser superior al nivel anterior. Esto se ilustra en la Figura\(\PageIndex{2}\). Observe lo cerca que está el nivel donante de la banda de conducción y que el nivel Fermi ha sido empujado hacia arriba, lejos de la banda de valencia y más cerca de la banda de conducción. Esto será de gran importancia en las próximas discusiones sobre dispositivos semiconductores.
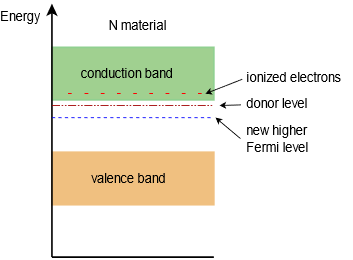
Figura\(\PageIndex{2}\): Diagrama de banda de energía del semiconductor tipo N.
1.4.2: Material Tipo P
De manera similar, si introducimos una impureza trivalente, nuestro modelo cristalino cuenta ahora con un agujero; una ubicación donde falta un electrón. Por esta razón, las impurezas trivalentes a veces se llaman aceptores. El modelo cristalino resultante se ilustra en la Figura\(\PageIndex{3}\).
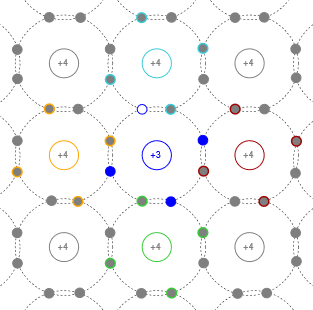
Figura\(\PageIndex{3}\): Cristal con impureza trivalente añadida (tipo P).
La situación resultante es esencialmente la inversa de la del material tipo N. La figura\(\PageIndex{4}\) muestra el diagrama de bandas de energía para nuestro nuevo material tipo P. En este caso, el nivel Fermi ha sido empujado hacia abajo, más cerca de la banda de valencia.
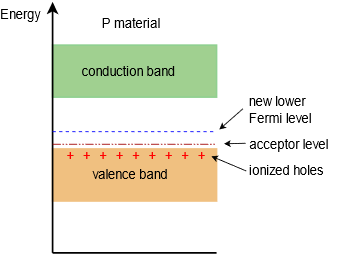
Figura\(\PageIndex{4}\): Diagrama de banda de energía del semiconductor Ptype.
En material de tipo P, los agujeros hacia fuera número de electrones libres. En consecuencia, los agujeros son referidos como el portador mayoritario en el material P, mientras que los electrones asumen el papel de portador de carga minoritaria.
Al igual que con el material tipo N, cuanto mayor sea la cantidad de impureza trivalente añadida, mayor será el efecto general. Por sí mismo, se puede usar un cristal dopado para crear una resistencia. La resistividad del material es una función del nivel de dopaje. Al establecer el área de la sección transversal, la longitud y el nivel de dopaje, podemos crear valores de resistencia bien definidos. Si esto fuera todo lo que pudiéramos hacer con los semiconductores entonces podríamos decir dos cosas: primero, la revolución de semiconductores de estado sólido no existiría; y segundo, este texto sería muy corto. Los bits interesantes llegan cuando combinamos materiales de tipo N y P en un solo dispositivo, como comenzaremos a ver en el siguiente capítulo.
Referencias
1 Un ion es un átomo o molécula que no tiene una carga neta neutra, es decir, los números de protones y electrones no son iguales. Si pierde electrones, lo que resulta en una carga neta positiva, se le llama catión. Si gana electrones dando como resultado una carga neta negativa se le llama anión.


