5.5: Sesgo de retroalimentación
- Page ID
- 83377
Si bien la polarización del emisor de dos fuentes y la polarización del divisor de voltaje pueden producir una estabilidad muy alta, hay otras configuraciones de polarización disponibles. Su estabilidad tiende a no ser tan buena, pero son superiores al sesgo de base simple. También tienden a usar menos componentes que sus primos de alta estabilidad. Como grupo, nos referimos a estos como configuraciones de polarización de retroalimentación. Utilizan el concepto de retroalimentación negativa. Esta es una técnica donde un cambio en la salida puede reflejarse de nuevo a la entrada de tal manera que tiende a compensar parcialmente el cambio de salida.
5.5.1: Sesgo de retroalimentación del colector
Con un simple movimiento\(R_B\) en la configuración básica de sesgo base, llegamos al sesgo de retroalimentación del colector. La plantilla NPN se muestra en la Figura\(\PageIndex{1}\). En comparación con el sesgo base, todo lo que ha cambiado\(R_B\) es que está conectado a la parte inferior de\(R_C\) en lugar de a la fuente de alimentación. Ese pequeño cambio puede tener un efecto notable en la estabilidad.
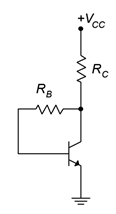
Figura\(\PageIndex{1}\): Sesgo de retroalimentación del recopilador.
Para entender cómo funciona la retroalimentación, supongamos que una corriente está fluyendo desde el suministro\(R_C\), a través, hacia el colector y finalmente, fuera del emisor a tierra. Vía KVL,\(V_{CE} = V_C = V_{CC} − I_C \cdot R_C\). Ahora supongamos por alguna razón, un cambio de temperatura tal vez,\(\beta\) aumenta. Esto debería provocar un aumento en\(I_C\). Un aumento en\(I_C\), sin embargo, provocaría un aumento en la caída\(R_C\) debido a la ley de Ohm. Esto, a su vez, obligaría\(V_C\) a caer. Aquí está la clave: también\(V_C\) es igual a la caída a través\(R_B\) más el voltaje\(V_{BE}\). El potencial base-emisor se fija a aproximadamente 0.7 voltios, por lo que cualquier disminución en\(V_C\) se refleja como una disminución en el voltaje a través\(R_B\). Por ley de Ohm, eso significa que\(I_B\) debe disminuir en una proporción similar. Esta disminución tiende a compensar la tendencia inicial de la corriente del colector a aumentar.
Para derivar una ecuación para la corriente de colector, podemos usar KVL.
\[V_{CC} = V_{R_C} +V_{R_B} +V_{BE} \\ V_{CC} = I_E R_C+I_B R_B+V_{BE} \\ V_{CC} = I_C R_C+ \frac{I_C}{\beta} R_B+V_{BE} \\ I_C = \frac{V_{CC} −V_{BE}}{R_C+R_B /\beta} \label{5.10} \]
Esta ecuación es muy similar a las derivaciones de corriente para la polarización del emisor de dos fuentes (Eq 5.3.1) y la polarización del divisor de voltaje (Eq 5.4.3). Nuevamente, si podemos establecer\(R_C \gg R_B/\beta\) entonces\(I_C\) será relativamente inmune a los cambios de punto Q debidos a\(\beta\). El problema aquí es que no es tan fácil cumplir con esa estipulación en este circuito. En consecuencia, la retroalimentación del colector tiende a tener solo una estabilidad modesta.
En cuanto a los puntos finales de corte y saturación en la línea de carga de CC, una vez más, el corte es determinado por la fuente de alimentación de CC mientras que la saturación está determinada por la cantidad de resistencia en el colector-emisor para limitar la corriente de dicha fuente de alimentación.
\[I_{C(sat)} = \frac{V_{CC}}{R_C} \label{5.11} \]
\[V_{CE (cutoff )} = V_{CC} \label{5.12} \]
Ejemplo\(\PageIndex{1}\)
Suponiendo\(\beta = 100\), determinar el punto Q (\(I_C\)y\(V_{CE}\)) para el circuito de la Figura\(\PageIndex{2}\). ¿Cuánto cambia el punto Q si\(\beta\) se reduce a la mitad?
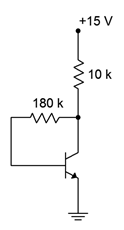
Figura\(\PageIndex{2}\): Circuito por Ejemplo\(\PageIndex{1}\).
Usando la ecuación\ ref {5.10}
\[I_C = \frac{V_{CC} −V_{BE}}{R_C+R_B /\beta} \nonumber \]
\[I_C = \frac{15 V−0.7 V}{10 k \Omega +180 k \Omega /100} \nonumber \]
\[I_C = 1.21 mA \nonumber \]
Uso de KVL
\[V_{CE} = V_{CC} −V_{RC} \nonumber \]
\[V_{CE} = V_{CC} −I_C R_C \nonumber \]
\[V_{CE} = 15V−1.21 mA\times 10 k \Omega \nonumber \]
\[V_{CE} = 2.9 V \nonumber \]
Si\(\beta\) se reduce a la mitad a 50
\[I_C = \frac{V_{CC} −V_{BE}}{R_C+R_B /\beta} \nonumber \]
\[I_C = \frac{15V−0.7V}{10 k \Omega +180 k \Omega /50} \nonumber \]
\[I_C = 1.05 mA \nonumber \]
\[V_{CE} = V_{CC} −I_C R_C \nonumber \]
\[V_{CE} = 15V−1.05 mA\times 10 k \Omega \nonumber \]
\[V_{CE} = 4.5 V \nonumber \]
Para una caída de 2:1 en\(\beta\) vemos una reducción de aproximadamente 13% en\(I_C\) con un cambio algo mayor en\(V_{CE}\). Este circuito claramente no es tan estable como la polarización del emisor de dos fuentes o la polarización del divisor de voltaje, pero es superior a la polarización base.
La versión PNP de la configuración del sesgo de retroalimentación del colector no debería ser ninguna sorpresa. La plantilla se muestra en la Figura\(\PageIndex{3}\). Aquí, utilizamos la misma técnica de cambio de fuente de alimentación que se utilizó con el divisor de voltaje PNP para terminar con una fuente de alimentación positiva. Al igual que con el divisor de voltaje PNP, debido a que hemos cambiado el punto de referencia, todos los voltajes referenciados a tierra serán diferentes de sus contrapartes NPN. Todas las corrientes y voltajes de componentes tendrán las mismas magnitudes pero con direcciones y polaridades opuestas.
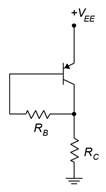
Figura\(\PageIndex{3}\): Sesgo de retroalimentación del colector PNP.
5.5.2: Sesgo de retroalimentación del emisor
El sesgo de retroalimentación del emisor utiliza la misma idea general que el circuito de retroalimentación del colector, es decir, que los cambios en la salida se reflejarán de nuevo a la entrada y, por lo tanto, ayudarán a mitigar el cambio inicial. Mientras que la retroalimentación del colector se centra en la corriente del colector que establece\(V_C\) vía\(R_C\), la retroalimentación del emisor utiliza el hecho de que la corriente del emisor establece\(V_E\) vía\(R_E\) En ambos casos, estos voltajes se utilizan para cambiar el voltaje a través\(R_B\), lo que resulta en un cambio en\(I_B\) que se opone al cambio de corriente del colector original.
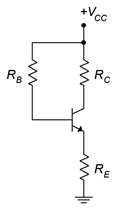
Figura\(\PageIndex{4}\): Sesgo de retroalimentación del emisor.
Un circuito básico de polarización de realimentación del emisor se muestra en la Figura\(\PageIndex{4}\). Utilizaremos KVL para desarrollar una ecuación para la corriente de colector.
\[V_{CC} = V_{R_B} +V_{BE}+V_{R_E} \\ V_{CC} = I_B R_B+V_{BE} + I_E R_E \\ V_{CC} = \frac{I_C}{\beta} R_B + I_C R_E+V_{BE} \\ I_C = \frac{V_{CC} −V_{BE}}{R_E+R_B /\beta} \label{5.13} \]
Si podemos establecer\(R_E \gg R_B/\beta\) entonces el punto Q será estable a pesar de los cambios en\(\beta\). El problema aquí es el mismo que fue el caso en la retroalimentación de los recopiladores, es decir, que esta estipulación no es fácil de lograr. En consecuencia, la configuración de retroalimentación del emisor tiende a tener solo una estabilidad modesta. En cualquier caso, una vez que se conoce la corriente del colector, se\(V_{CE}\) puede encontrar utilizando las técnicas ilustradas con la configuración del divisor de tensión. Los puntos finales para la línea de carga de CC se encuentran de la manera habitual.
\[I_{C(sat)} = \frac{V_{CC}}{R_C+R_E} \label{5.14} \]
\[V_{CE (cutoff )} = V_{CC} \label{5.15} \]
Ejemplo\(\PageIndex{2}\)
Suponiendo\(\beta\) = 100, determinar el punto Q (\(I_C\)y\(V_{CE}\)) para el circuito de la Figura\(\PageIndex{5}\).
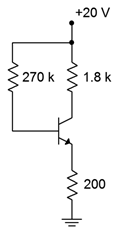
Figura\(\PageIndex{5}\): Circuito por Ejemplo\(\PageIndex{2}\).
Usando la ecuación\ ref {5.13}
\[I_C = \frac{V_{CC} −V_{BE}}{R_E+R_B /\beta} \nonumber \]
\[I_C = \frac{20 V−0.7V}{200 \Omega +270 k \Omega /100} \nonumber \]
\[I_C = 6.66 mA \nonumber \]
Uso de KVL
\[V_{CE} = V_{CC} −V_{R_C} −V_{R_E} \nonumber \]
\[V_{CE} = V_{CC} −I_C (R_C+R_E ) \nonumber \]
\[V_{CE} = 20 V−6.66mA(1.8 k \Omega +200 \Omega ) \nonumber \]
\[V_{CE} = 6.68 V \nonumber \]
Para completar la línea de carga, encontramos
\[I_{C(sat)} = 10 mA \nonumber \]
\[V_{CE(cutoff)} = 20 V \nonumber \]
\(\beta\)Bajar a 50 resultará en
\[I_C = 3.45 mA \nonumber \]
\[V_{CE} = 13.1 V \nonumber \]
Vemos menos de un cambio de 2:1 en\(I_C\) y\(V_{CE}\) pero la estabilidad no es dramática.
5.5.3: Sesgo combinado de retroalimentación
La configuración de polarización de retroalimentación final combina tanto la retroalimentación del colector como la retroalimentación del emisor para llegar al circuito representado en la Figura\(\PageIndex{6}\). Le otorgaremos el nombre altamente original del sesgo de retroalimentación combinada.
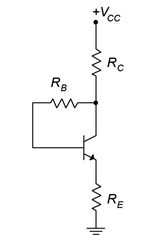
Figura\(\PageIndex{6}\): Sesgo de retroalimentación de combinación.
Este circuito aplica retroalimentación\(R_B\) desde ambos extremos, por así decirlo, por lo que tiende a tener una estabilidad ligeramente mejor que la retroalimentación del colector o el sesgo de retroalimentación del emisor. Por supuesto, ahora es solo una resistencia tímida del circuito divisor de voltaje que es considerablemente más estable.
Las ecuaciones para la línea de carga se enumeran a continuación. Las derivaciones se dejan como ejercicio.
\[I_C = \frac{V_{CC} −V_{BE}}{R_C+R_E+R_B /\beta} \label{5.16} \]
\[V_{CE} = V_{CC} −I_C (R_C+R_E ) \label{5.17} \]
\[I_{C(sat)} = \frac{V_{CC}}{R_C+R_E} \label{5.18} \]
\[V_{CE (cutoff )} = V_{CC} \label{5.19} \]
Ejemplo\(\PageIndex{3}\)
Suponiendo\(\beta = 125\), determinar el punto Q (\(I_C\)y\(V_{CE}\)) para el circuito de la Figura\(\PageIndex{7}\).
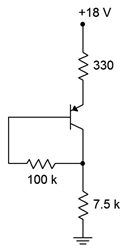
Figura\(\PageIndex{7}\): Circuito por Ejemplo\(\PageIndex{3}\).
Tenga en cuenta que esta es la versión PNP al revés. Usando la ecuación\ ref {5.16}
\[I_C = \frac{V_{CC} −V_{BE}}{R_C+R_E+R_B /\beta} \nonumber \]
\[I_C = \frac{18 V−0.7V}{7.5 k \Omega +330 \Omega +100 k \Omega / 125} \nonumber \]
\[I_C = 2mA \nonumber \]
Uso de KVL
\[V_{CE} = V_{CC} −V_{R_C} −V_{R_E} \nonumber \]
\[V_{CE} = V_{CC} −I_C (R_C+R_E ) \nonumber \]
\[V_{CE} = 18V−2 mA(7.5 k \Omega +330 \Omega ) \nonumber \]
\[V_{CE} = 2.34 V \nonumber \]


