6.2: Modelo de amplificador

El amplificador ideal no hace nada excepto aumentar la amplitud de la señal de entrada. El factor de aumento se define como la relación entre la señal de salida y la señal de entrada. Es una cantidad sin unidades. Por ejemplo, si la señal de entrada tiene una potencia de 10 milivatios y el circuito aumenta la señal hasta 50 milivatios, decimos que tiene una ganancia de potencia de 50 milivatios /10 milivatios, o 5. De igual manera, si la señal de entrada es de 2 voltios y la señal de salida es de 16 voltios, decimos que tiene una ganancia de voltaje de 16 voltios/2 voltios, o de 8. Históricamente, la ganancia de poder se denota como\(G\). Para ganancia de voltaje y ganancia de corriente utilizamos\(A_v\) y\(A_i\), donde\(A\) significa factor de\(A\) mplificación. Algunos amplificadores invierten la señal de entrada a salida. Básicamente, dan la vuelta a la forma de onda boca abajo. Para una onda sinusoidal simple esto equivale a desplazar la fase de la señal en 180\(^{\circ}\), y para una entrada de onda sinusoidal el amplificador produce una salida −sine. Para reflejar este efecto, el factor de amplificación se denota como negativo. Por ejemplo, un\(A_v\) de −10 indica un factor de amplificación de 10 con una inversión de señal.

El tamaño y la complejidad de un circuito amplificador pueden variar considerablemente, desde un solo transistor hasta docenas de transistores. Para facilitar el diseño del sistema, es útil utilizar modelos funcionales simplificados. Por lo general, estos modelos utilizan una resistencia para representar la impedancia vista mirando al amplificador junto con una fuente controlada y su resistencia interna asociada. Un ejemplo se muestra en la Figura\(\PageIndex{1}\).

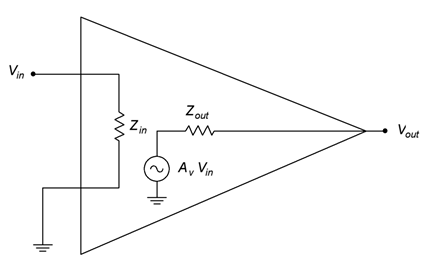
Figura\(\PageIndex{1}\): Un modelo de amplificador de voltaje simple.

Este es un modelo de un amplificador de voltaje (tenga en cuenta que\(V_{in}\) y\(V_{out}\) se especifican junto con una fuente de voltaje controlada dentro del modelo). La fuente de voltaje controlado y su serie\(Z_{out}\) es el equivalente Thevenin de la salida cuando se ve desde la carga (es decir, el\(V_{out}\) pin). Asimismo,\(Z_{in}\) es la impedancia equivalente vista por la fuente de accionamiento. Debido a que un amplificador de voltaje está diseñado para maximizar la transferencia de voltaje, la impedancia de entrada tiende a ser alta para minimizar la carga (piense en un voltímetro). Del mismo modo, la impedancia de salida tendería a ser baja (piense en una fuente de voltaje ideal). En contraste, un circuito diseñado para la máxima transferencia de corriente tendería a tener un bajo\(Z_{in}\) y otro alto\(Z_{out}\). Precisamente cómo el circuito crea el impulso de señal no es una preocupación de este modelo, solo nos importa que sí.

6.2.1: Efectos de carga

Una vez establecido el modelo es relativamente fácil reconocer y calcular los efectos de carga. Los efectos de carga son pérdidas de señal causadas por interacciones entre las impedancias del amplificador y las de los circuitos y cargas conectadas a él. En la Figura se muestra un modelo genérico que incluye efectos de carga\(\PageIndex{2}\).

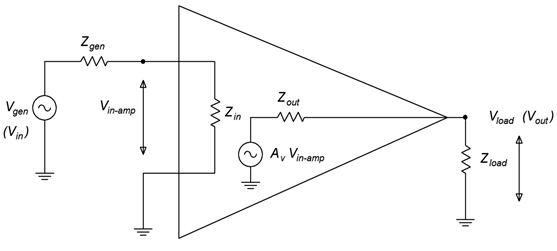
Figura\(\PageIndex{2}\): Modelo de amplificador de voltaje con efectos de carga.

Un examen superficial de la Figura\(\PageIndex{2}\) muestra que hay un divisor de voltaje entre\(Z_{gen}\) y\(Z_{in}\) junto con un segundo divisor entre\(Z_{out}\) y\(Z_{load}\). Cada uno de estos divisores provoca pérdida de señal, es decir, reducen el voltaje de salida final. El voltaje de entrada al amplificador se reduce de la siguiente manera

\[V_{i n−amp} = \frac{Z_{i n}}{Z_{i n}+Z_{gen}} \times V_{gen} \nonumber \]

El voltaje de carga se reduce de la siguiente manera

\[V_{load} = \frac{Z_{load}}{Z_{load} + Z_{out}} \times A_v \times V_{i n−amp} \nonumber \]

Por lo tanto, la ganancia combinada es

\ [A_ {sistema} =\ frac {V_ {carga}} {V_ {gen}} =\ frac {Z_ {i n} {Z_ {i n} + Z_ {gen}}\ veces a_V\ veces\ frac {Z_ {carga}} {Z_ {carga} +Z_ {fuera}}

Para minimizar estas pérdidas nos gustaría\(Z_{in} \gg Z_{gen}\) y\(Z_{load} \gg Z_{out}\).

Ejemplo\(\PageIndex{1}\)

Un amplificador de voltaje tiene las siguientes especificaciones:\(A_v=20\),\(Z_{in}=10\) k\(\Omega \),\(Z_{out}=200 \Omega \). Es impulsado por una fuente de 30 milivoltios con una impedancia\(\Omega \) interna de 600 y acciona una\(\Omega \) carga de 1 k. Determine el voltaje de carga.

El voltaje que aparece en la entrada del amplificador es

\[V_{i n−amp} = \frac{Z_{i n}}{Z_{i n} + Z_{gen}} \times V_{gen} \nonumber \]

\[V_{i n−amp} = \frac{10 k \Omega}{ 10 k\Omega +600 \Omega} \times 30 mV \nonumber \]

\[V_{i n−amp} = 28.3 mV \nonumber \]

Esto se multiplica por la ganancia de voltaje de 20 y luego se reduce por el divisor de salida.

\[V_{i n−amp} = \frac{Z_{load}}{Z_{load} +Z_{out}} \times A_v \times V_{i n−amp} \nonumber \]

\[V_{i n−amp} = \frac{1 k\Omega}{1k \Omega +200 \Omega} \times 20\times 28.3mV \nonumber \]

\[V_{i n−amp} = 471.7mV \nonumber \]

Sin los efectos de carga, la señal de salida sería simplemente 30 milivoltios veces la ganancia de voltaje de 20, o 600 milivoltios. Además, tenga en cuenta que si la fuente es reemplazada por un generador de función de grado de laboratorio típico que exhibe una impedancia interna de 50\(\Omega \) y se elimina la carga, siendo reemplazada por un osciloscopio que exhibe una impedancia de\(\Omega \) entrada típica de 1 M, los efectos de carga serían mínimos y nosotros lo haríamos medir solo unos milivoltios por debajo de los 600 milivoltios ideales.