6.3: Cumplimiento y distorsión
- Page ID
- 83427
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En algún momento la idealización de que la señal de salida es meramente la señal de entrada veces falla la ganancia. Todos los amplificadores tienen un límite en lo grande que puede ser la señal de salida. Esto es establecido por la fuente de alimentación de CC y el diseño del amplificador. La señal de salida máxima (típicamente, la tensión de salida máxima) se conoce como el cumplimiento. Cualquier intento de producir una señal de salida que oscile más allá del cumplimiento dará como resultado una distorsión de la forma de onda. En el caso más simple, la señal de salida se limita estricta y abruptamente al nivel de cumplimiento y se eliminará cualquier porción de la forma de onda de salida que de otro modo estaría por encima de esa. Es como si alguna forma de tijera electrónica recortara la parte superior de la forma de onda. Por lo tanto, esto a menudo se conoce como recorte. Un ejemplo de recorte se ilustra en la Figura\(\PageIndex{1}\). La forma de onda de salida ideal se muestra en marrón y la forma de onda recortada se muestra en azul. El recorte es tan severo aquí que la forma de onda recortada ahora se parece menos a una onda sinusoidal y más a una onda cuadrada. Esto es una distorsión extrema de la forma de onda y tiene consecuencias importantes.
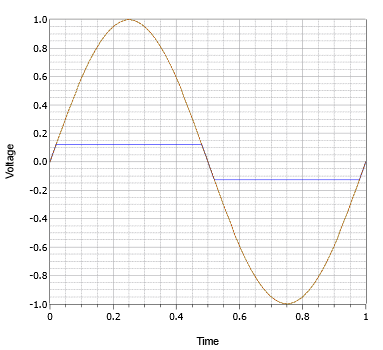
Figura\(\PageIndex{1}\): Forma de onda recortada.
Siempre que se altere una señal en el dominio del tiempo, habrá una alteración de su contenido de frecuencia. Dependiendo de lo que iniciamos y de la manera en que se altere la forma de onda, se pueden agregar nuevos componentes de frecuencia a la señal y los niveles de los componentes existentes pueden cambiarse o incluso eliminarse. El recorte extremo que creó una onda cercana al cuadrado agregó una gran cantidad de nuevos componentes de frecuencia a la señal.
Para ver cómo se conectan la forma de onda y el contenido de frecuencia, considere la forma de onda representada en la Figura\(\PageIndex{2}\). Comenzamos con una onda sinusoidal simple que se muestra en verde. Nos referimos a esto como la frecuencia fundamental o base. Luego agregamos un armónico. Un armónico es otra onda sinusoidal que es un múltiplo entero de la frecuencia fundamental. Puede ser mayor o menor en amplitud y la fase puede ser desplazada. En este ejemplo tenemos un solo seno a tres veces la frecuencia fundamental (azul). Cuando agregamos este armónico a lo fundamental llegamos a una nueva forma de onda que se muestra en rojo. Esta nueva forma de onda parece algo así como una onda cuadrada pero con una parte superior e inferior “grumosa”. Si agregamos más armónicos, estas variaciones comenzarán a suavizarse, como se muestra en la Figura\(\PageIndex{3}\). Esta forma de onda parece estar bastante cerca de una onda cuadrada y no muy distante de nuestra forma de onda recortada anterior. En base a esto, podemos concluir que la onda sinusoidal recortada tiene nuevos componentes de frecuencia agregados a la misma. También podemos concluir que si nuestro amplificador recorta una forma de onda más complicada como un fragmento de música, ese proceso agregará nuevos armónicos también. Además, es probable que estos armónicos sean audibles y puedan cambiar nuestra percepción de la música, quizás sutilmente pero quizás drásticamente.
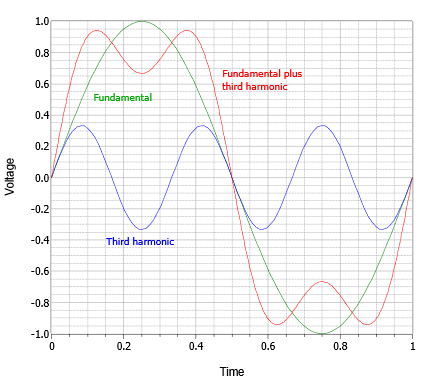
Figura\(\PageIndex{2}\): Onda sinusoidal con tercer armónico.
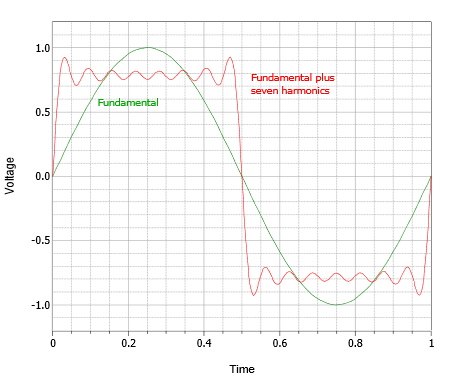
Figura\(\PageIndex{3}\): Onda sinusoidal con siete armónicos, acercándose a una onda cuadrada.
Junto con el recorte, los amplificadores pueden exhibir formas más sutiles de distorsión debido a la no linealidad interna. Por ejemplo, es posible que la ganancia varíe ligeramente a medida que la señal oscila de baja a alta o de negativa a positiva. Un ejemplo se muestra en la Figura\(\PageIndex{4}\) con la onda distorsionada mostrada en rojo.
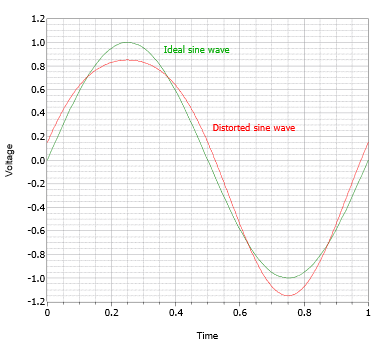
Figura\(\PageIndex{4}\): Onda sinusoidal con distorsión.
A primera vista puede parecer como si la ola estuviera simplemente compensada negativamente. Este no es el caso. Si desplazamos la onda verticalmente, como en la Figura\(\PageIndex{5}\), se hace evidente que la onda está verdaderamente distorsionada y ya no es una onda sinusoidal pura.
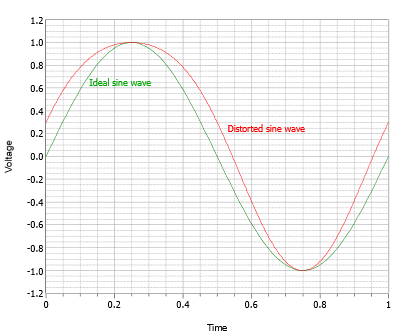
Figura\(\PageIndex{5}\): Onda sinusoidal con distorsión, nivel desplazado.
A diferencia de la onda recortada, la onda distorsionada en la Figura\(\PageIndex{5}\) exhibe una asimetría; la porción negativa no parece ser una imagen especular de la porción positiva. En otras palabras, esta onda carece de simetría de media onda. Las ondas que exhiben simetría de media onda contienen solo distorsión armónica impar (armónicos que son múltiplos enteros impares de lo fundamental). En contraste, las ondas que carecen de media simetría tienen al menos un armónico par. Aquí se explica cómo probar la simetría de media onda. Primero, considere la onda en diente de sierra que se muestra en la Figura\(\PageIndex{6}\).
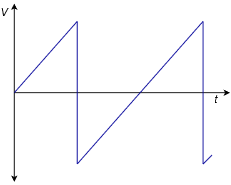
Figura\(\PageIndex{6}\): Prueba de simetría de media onda: Onda en diente de sierra.
Gire la porción negativa de la onda alrededor del eje de tiempo como se muestra en la Figura\(\PageIndex{7}\).
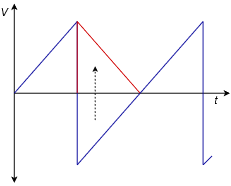
Figura\(\PageIndex{7}\): Prueba de simetría de media onda: Onda en diente de sierra, porción negativa girada.
Finalmente, deslice la porción negativa sobre la porción positiva y vea si son idénticas, como en la Figura\(\PageIndex{8}\).
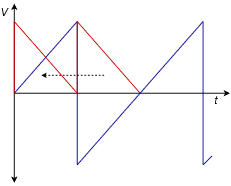
Figura\(\PageIndex{8}\): Prueba de simetría de media onda: Onda en diente de sierra, porción negativa girada y deslizada.
Si las dos mitades son idénticas entonces la onda tiene simetría de media onda. La onda en diente de sierra no presenta simetría de media onda, por lo tanto, debe contener al menos un armónico par.
La linealidad de un amplificador a menudo se cuantifica a través de una medición de Distorsión Armónica Total, o THD. La medición se realiza aplicando una onda sinusoidal muy pura y de baja distorsión al amplificador. Esto es lo fundamental. A la salida del amplificador, se utiliza un filtro muy selectivo para eliminar lo fundamental. Esto deja atrás solo los armónicos de distorsión añadidos. 1 Estos armónicos se tratan luego como un valor agrupado y se presentan como un porcentaje de la señal total. En un osciloscopio, es relativamente fácil para una persona discernir los niveles de THD en los dos dígitos. Por otro lado, es muy difícil, si no imposible, para un individuo discernir niveles de THD muy por debajo del 1% a ojo. Por supuesto, lo que importa es lo que podemos escuchar, no cómo se ve la forma de onda. Para poner esto en perspectiva, muchos amplificadores de audio de alta fidelidad exhiben niveles de THD por debajo de 0.1% mientras que un amplificador de guitarra sobrealimentado podría estar funcionando más del 20%. Sin embargo, THD no es la última palabra sobre distorsión. Tiene sus límites. Por ejemplo, todos los productos de distorsión están agrupados. No dice nada sobre qué armónicos son particularmente fuertes o su distribución. Tampoco dice mucho sobre lo que sucede cuando interactúan múltiples frecuencias. Un método para tratar de cuantificar eso es aplicar dos ondas sinusoidales a diferentes frecuencias al amplificador simultáneamente. El resultado se llama una clasificación de distorsión de intermodulación, o IMD. Esto también se expresa como un porcentaje.
Referencias
1 Para ser estrictamente precisos, el residual consiste en los armónicos más cualquier ruido producido por el amplificador. Por lo tanto, es más preciso referirse a esto como una especificación de ruido THD+.


