9.2: La configuración de clase B

La operación de clase B se define como tener un flujo de corriente de colector de CA 180\(^{\circ}\) fuera del ciclo. En consecuencia, para amplificar toda la señal, se necesitarán dos dispositivos. Además, tendremos que prestar atención a cómo las dos mitades de forma de onda están “cosidas” ya que esto podría ser un área problemática. La pregunta obvia en este punto es, ¿por qué nos molestamos en separar las medias ondas positivas y negativas si esto conlleva complejidad del circuito y posibles problemas de forma de onda? La respuesta es mejorar la eficiencia.

En el capítulo anterior descubrimos que los amplificadores de clase A no son eficientes. De hecho, en el mejor de los casos solo transforman el 25% de la potencia de entrada de CC en potencia de carga útil. ¿Por qué ocurre esto y cómo aborda la topología de clase B esta situación?

La idea básica de la clase B es empujar el punto Q hacia abajo para que quede justo en el punto de corte en la línea de carga de CA. Esto significa que\(I_{CQ}\) es 0 A y prácticamente no se extrae energía de la fuente al ralentí. Ubicar el punto Q en el punto de corte también significa que el transistor recortará inmediatamente la porción negativa de la onda. En consecuencia, necesitaremos un circuito de imagen especular para producir esa porción (y que recortará la porción positiva).

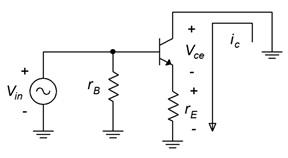
Figura\(\PageIndex{1}\): Circuito de CA simplificado seguidor de voltaje.

Para comprender mejor cómo funciona la operación de clase B, considere el circuito de CA simplificado de un seguidor de voltaje que se muestra en la Figura\(\PageIndex{1}\). Si situamos el punto Q directamente en\(v_{CE(cutoff)}\) entonces el asociado\(I_{CQ}\) es 0 A. A medida que la señal de entrada oscila positiva, la corriente del colector aumenta. A medida que lo hace, el voltaje a través de la carga\((r_E)\) comienza a aumentar y el voltaje a través del colector-emisor del transistor comienza a disminuir (debido a KVL). Cuando la señal de entrada oscila en negativo, el transistor se apaga. Como resultado, no se crea corriente de colector, no se desarrolla voltaje a través de la carga y\(v_{CE}\) permanece en el corte. Es como si la forma de onda de entrada hubiera sido rectificada de media onda. Esta acción se muestra en la Figura\(\PageIndex{2}\). A medida que la señal de entrada oscila positivamente, el punto de operación se desliza hacia arriba por la línea de carga, moviéndose hacia la saturación, y esta corriente incrementada crea un voltaje de carga que sigue a la señal de entrada. En contraste, cuando la entrada intenta balancearse negativa, no hay lugar más para ir en la línea de carga y la porción negativa de la ola simplemente se recorta.

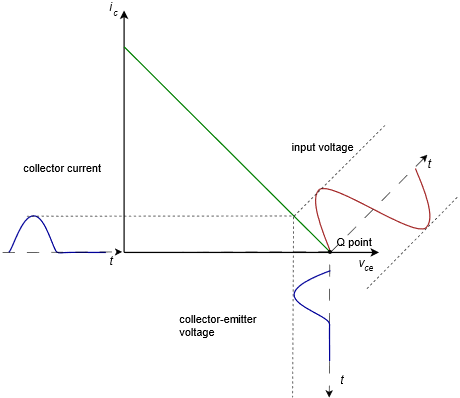
Figura\(\PageIndex{2}\): Línea de carga de CA para operación de clase B.

Si hiciéramos una versión PNP del circuito representado en la Figura\(\PageIndex{1}\), sucedería exactamente lo contrario: el amplificador reproduciría la porción negativa de la onda y recortaría la porción positiva. La siguiente pregunta es, ¿cómo polarizamos el transistor en el punto de corte y empalmamos las versiones NPN y PNP en un todo viable?

Empecemos por hacer dos seguidores emisores desnudos, uno NPN y el otro PNP. Conectaremos sus emisores juntos y ataremos eso a la carga. Conectaremos el colector del NPN directamente a una fuente de CC y el colector del PNP a tierra. Recuerda, las resistencias de colector no serán necesarias porque estas son seguidores. No incluiremos componentes de polarización en la base porque queremos\(I_{CQ}\) establecer en 0 A. También tendremos que agregar condensadores de entrada y salida para evitar que la fuente y la carga cortocircuiten inadvertidamente o deriven partes del circuito de CC. El resultado se ve en la Figura\(\PageIndex{3}\).

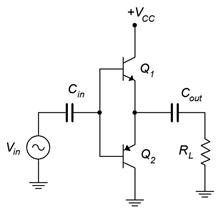
Figura\(\PageIndex{3}\): Circuito Prototipo Clase B.

Sin señal suministrada, ambos transistores deben estar apagados. Esto se debe a que sus bases están unidas entre sí, y sin algún otro potencial aplicado, ambas tensiones base-emisor deben ser cero. Suponiendo\(Q_1\) y\(Q_2\) coincidiendo, el voltaje de la fuente de alimentación debe dividirse uniformemente entre ellos, dejando la mitad de\(V_{CC}\) en los emisores. Este potencial también aparece a través\(C_{out}\), evitando que el voltaje de CC alcance\(R_L\).

Cuando la señal de entrada sale positiva, sube\(V_{B1}\) y\(V_{B2}\) por encima de 0.5\(V_{CC}\). Esto\(Q_2\) se mantiene apagado pero se enciende\(Q_1\). La corriente ahora es libre para fluir hacia abajo a través\(Q_1\) y hacia la carga. Cuando la señal de entrada oscila en negativo, ocurre lo inverso:\(Q_1\) se apaga y\(Q_2\) se enciende. Esto permite que la corriente fluya hacia arriba desde la carga y hacia abajo\(Q_2\) (si esto es confuso, recuerde que ya se había establecido un voltaje de CC\(C_{out}\) que es igual a 0.5\(V_{CC}\) y esto es lo que permite que la corriente fluya desde tierra hacia arriba\(R_L\) y luego hacia abajo a través \(Q_2\)como\(Q_2\) comienza a conducir). Se puede pensar en\(Q_1\) introducir corriente en la carga (abastecimiento) y\(Q_2\) extraer corriente de la carga (hundimiento). En consecuencia, los amplificadores de clase B a veces se denominan amplificadores push-pull.

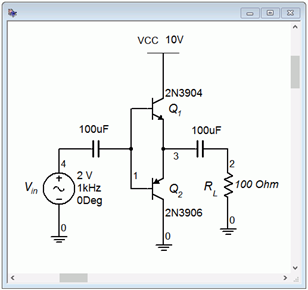
Figura\(\PageIndex{4}\): Prototipo de circuito Clase B en simulador.

Para ver qué tan bien funciona este prototipo, ingresaremos una versión en un simulador, como se muestra en la Figura\(\PageIndex{4}\). Se realiza un análisis transitorio con los resultados mostrados en la Figura\(\PageIndex{5}\).

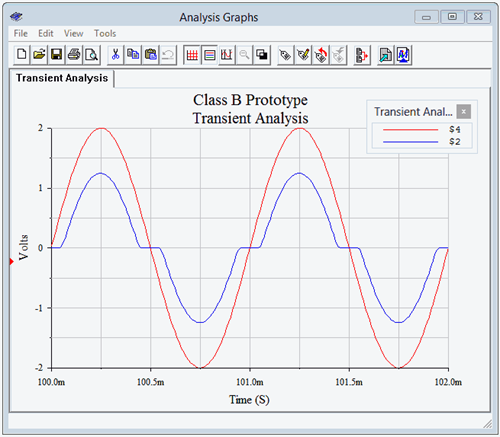
Figura\(\PageIndex{5}\): Análisis transitorio del prototipo de circuito Clase B.

Claramente, hay problemas con la forma de onda de salida (nodo 2, en azul). En primer lugar, la amplitud de la señal es notablemente menor que la señal de entrada de pico de 2 voltios. El segundo problema es el extraño “manchado plano” de la forma de onda de salida cerca de los puntos de cruce por cero. Resulta que estos dos problemas son manifestaciones de la misma causa raíz. Si miramos cuidadosamente los picos, podemos obtener una pista de lo que está pasando. El voltaje de salida pico es aproximadamente 0.75 voltios por debajo de la entrada, o solo alrededor de un potencial directo de unión PN. El problema es que la señal de entrada no encenderá realmente el transistor NPN hasta que la señal supere aproximadamente 0.7 voltios o caiga por debajo de −0.7 voltios para el lado PNP. Esa región entre −0.7 voltios y +0.7 voltios es una zona muerta a la que el amplificador no responderá. Esencialmente, el amplificador “arranca” cualquier cosa entre\(\pm\) 0.7 voltios. Esta es una forma burda de distorsión y tiene muchos nombres, incluida la distorsión de muesca y la distorsión cruzada. La parte particularmente desagradable de esta forma de distorsión es que golpea señales pequeñas peor que las señales grandes. La mayoría de las otras formas de no linealidades tienden a empeorar a medida que aumenta el nivel de señal.

9.2.1: Operación Clase AB

La solución básica a este problema es proporcionar una pequeña corriente de ralentí para que los transistores estén casi encendidos. De esta manera, solo se necesitará una señal de entrada muy pequeña para encender los dispositivos. Como esto aumentaría ligeramente el ángulo de conducción, esta forma de operación se conoce como operación de clase AB. Una solución potencial es agregar un divisor de voltaje como se representa en la Figura\(\PageIndex{6}\).

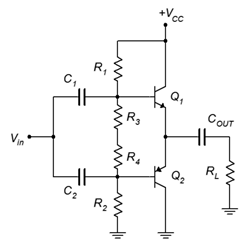
Figura\(\PageIndex{6}\): Circuito Prototipo Clase AB.

Este circuito utiliza una disposición simétrica: todo lo que está por encima de una línea horizontal dibujada a través del medio es repetido por un componente debajo de la línea. En otras palabras,\(R_1 = R_2\),\(R_3 = R_4\)\(C_1 = C_2\),,\(Q_1\) y\(Q_2\) son un par complementario. El divisor está configurado de manera que el voltaje cae a través\(R_3\) y\(R_4\) son de aproximadamente 0.7 voltios cada uno.

Diseñado correctamente, el circuito de la Figura\(\PageIndex{6}\) reducirá la distorsión de muesca. Desafortunadamente, tiene otros problemas. El primer problema involucra a los tres capacitores. \(C_{OUT}\)en particular podría ser bastante grande. Estos se pueden quitar si acudimos a una fuente de alimentación bipolar simétrica. En lugar de poner el colector del PNP a tierra, lo ataremos a una fuente de CC negativa. Para mantener el mismo voltaje total,\(Q_1\) estableceremos el colector en la mitad del original\(V_{CC}\) y el colector\(Q_2\) del original a la mitad del original\(V_{CC}\) pero negativo. En el lado de entrada, podríamos ejecutar la señal de entrada a la unión de\(R_3\) y\(R_4\).

El segundo tema que plaga al circuito de la Figura\(\PageIndex{6}\) es la estabilidad del sesgo. Las resistencias divisoras de voltaje tienen que ser muy precisas para poder establecer los transistores justo donde los queremos y la estabilidad es una preocupación. El problema es que estamos tratando de usar un dispositivo con una característica lineal de corriente-voltaje (una resistencia) para que coincida con la característica exponencial de corriente-voltaje de una unión PN. Este problema se ve agravado por el hecho de que estos dispositivos derivarán con la temperatura, y derivarán de diferentes maneras. La solución a este problema es utilizar un dispositivo con mejores características coincidentes. ¿Qué mejor dispositivo para hacer coincidir una unión PN que otra unión PN?

9.2.2: El espejo actual

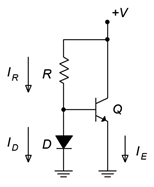
Figura\(\PageIndex{7}\): Un simple espejo de corriente.

Considere el circuito que se muestra en la Figura\(\PageIndex{7}\). A esto se le llama espejo de corriente. Así es como funciona: Primero, mira el divisor entre\(R\) y\(D\). El voltaje transversal\(R\) debe ser igual al voltaje de suministro menos la caída del diodo, o aproximadamente\(V − 0.7\). Esto establece una corriente,\(I_R\). Si la corriente base es lo suficientemente pequeña como para ignorarla, esta misma corriente fluye hacia abajo a través del diodo como\(I_D\). Esta corriente de diodo establece un voltaje específico a través del diodo (en algún lugar cercano a 0.7 voltios aunque el voltaje exacto no es importante). Porque el diodo está en paralelo con la unión base-emisor, entonces\(V_{BE} = V_D\). Si la curva de transconductancia (curva I-V) del transistor es idéntica a la del diodo, entonces la corriente del emisor debe ser la misma que la corriente del diodo. Cualquier cambio en la corriente del diodo provocaría un ligero cambio en el voltaje del diodo, y dado que el voltaje del diodo y el voltaje base-emisor son los mismos, entonces la corriente del emisor debe cambiar en respuesta. En otras palabras, la corriente del emisor refleja la corriente del diodo. Podemos programar la corriente del diodo (y por lo tanto, la corriente del emisor) estableciendo un valor apropiado para\(R\). Cualquiera que sea la corriente a través\(R\), esa es también la corriente de colector.

La idea del espejo de corriente se utiliza con gran efecto en circuitos integrados donde es fácil igualar las características del dispositivo. Cuando se trata de componentes discretos, no es tan fácil hacer coincidir un diodo con un transistor. Afortunadamente, no tenemos que tener una pareja perfecta. Simplemente usar cualquier diodo de señal proporcionará una combinación mucho mejor\(V_{BE}\) que usar una resistencia. Aunque la corriente del diodo no coincidirá con la corriente del colector precisamente, la polarización será más estable y los componentes rastrearán mucho mejor que cuando se usa una resistencia.

Combinar estas ideas nos lleva al circuito de la Figura\(\PageIndex{8}\). Este es nuestro primer amplificador práctico de clase B con el potencial de valores decentes de distorsión y estabilidad.

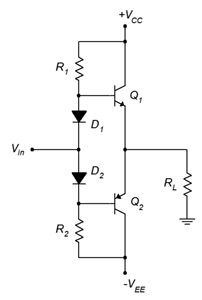
Figura\(\PageIndex{8}\): Amplificador Clase B con polarización de diodo y fuentes bipolares.

Una cosa que a veces molesta a las personas cuando ven por primera vez un amplificador polarizado por diodos es cómo la señal de CA pasará a través de los diodos a las bases. A primera vista, parece que la porción positiva de la señal de entrada estaría “yendo por el camino equivocado” contra el diodo\(D_1\). Lo que debemos recordar es que ya\(D_1\) está polarizado hacia adelante debido al suministro de CC y las resistencias circundantes. La señal no verá un abierto, verá la resistencia dinámica del diodo. ²

9.2.3: Máximos de Circuito Clase B

Ahora que tenemos un circuito viable, necesitamos derivar fórmulas para los puntos finales de la línea de carga de CA, significado\(v_{CE(cutoff)}\) y\(i_{C(sat)}\), y determinar el cumplimiento. El primer punto de nota es de corte. Debido a que los dos transistores dividirán el suministro disponible, siempre\(V_{CEQ}\) será igual a la mitad del suministro total. Además, hemos sesgado estos dispositivos en el punto de corte, y por lo tanto

\[v_{CE(cutoff)} = V_{CEQ} = 0.5 \cdot \text{ Total DC Supply} \label{9.1} \]

En el caso de un suministro bipolar, eso es lo mismo que uno de los dos lados. Debido a que la clase B usa dos transistores, la conformidad máxima será la misma que la de corte.

\[Compliance_{peak} = V_{CEQ} = 0.5 \cdot \text{ Total DC Supply} \label{9.2} \]

El voltaje nominal máximo de los transistores ocurrirá cuando estén apagados. En ese caso, si el transistor opuesto está completamente conductor, tendrá un voltaje insignificante a través de su colector-emisor. En consecuencia, el transistor de estado apagado puede ver toda la fuente de alimentación.

\[BV_{CEO} = \text{ Total DC Supply} \label{9.3} \]

La corriente de saturación viene dictada por el cumplimiento y la carga. Lo único que limita la corriente AC es la carga. Por lo tanto

\[i_{C(sat )} = \frac{Compliance_{peak}}{r_L} \label{9.4} \]

En base a eso, podemos decir

\[P_{load (max)} = \frac{{Compliance_{RMS}}^2}{r_L} \label{9.5} \]

Antes de ir más lejos, hay un ítem importante a tener en cuenta sobre el circuito de Figura\(\PageIndex{8}\) (y las variantes que discutiremos). Si echas otro vistazo al circuito verás que no hay nada en la línea colector-emisor que limite la corriente CC. De hecho, si tuviéramos que trazar la carga de CC junto con la carga de CA, obtendríamos algo como Figura\(\PageIndex{9}\).

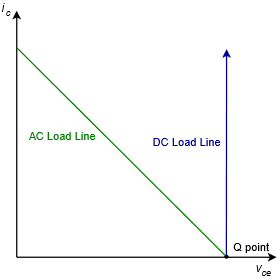
Figura\(\PageIndex{9}\): Comparación de líneas de carga de CA y CC para operación de clase B

La línea de carga de CC va hacia arriba. No hay ningún valor de corriente de saturación por debajo del infinito. Lo que esto realmente significa es que si no tenemos cuidado con el sesgo, es posible destruir los transistores. Lo mismo es cierto si accidentalmente acortamos la carga. Un rápido examen de las ecuaciones\ ref {9.4} y\ ref {9.5} muestra que una condición de carga cortocircuitada conduciría a enormes corrientes y potencias, y destruiría los transistores en el proceso. Con un amplificador de audio, esto podría suceder si uno de los hilos del cable del altavoz se desentrañara y tocara el cable adyacente. Obviamente, no es una situación feliz a menos que prefieras el olor a silicio quemado sobre el sonido de la música. Examinaremos los medios para proteger los transistores de sobrecargas accidentales más adelante en el capítulo.

9.2.4: Disipación de potencia Clase B

La disipación de potencia del transistor para la configuración de clase B es un poco más complicada que para la clase A. La disipación de potencia en reposo (punto Q) es muy baja. Se encuentra multiplicando\(I_{CQ}\) por\(V_{CEQ}\). \(I_{CQ}\)generalmente se establece en un poco por ciento de\(i_{C(sat)}\) lo que obviamente está muy por debajo de la potencia de carga máxima. A diferencia del diseño de clase A,\(P_{DQ}\) no representa el peor caso para la clase B.

Para determinar la disipación de potencia del transistor en el peor de los casos, comenzamos describiendo las formas de onda de corriente y voltaje durante la fase de conducción del NPN. La corriente de colector aparecerá como la mitad positiva de una onda sinusoidal. El caso máximo tiene la corriente que comienza en cero y alcanza el pico en\(i_{C(sat)}\) (o alternativamente,\(V_{CEQ}/r_L\)). Porque\(v_{CE}\), comienza en\(V_{CEQ}\) y luego se balancea hacia abajo a cero como medio seno negativo.

Nada dice que la caja de potencia de carga máxima debe provocar la disipación máxima del transistor. De hecho, vimos que este no era el caso de la clase A. En consecuencia, introduciremos un coeficiente,\(k\), que represente el porcentaje de la corriente máxima. Llegamos ahora a nuestras ecuaciones generales para la corriente y voltaje del transistor para el primer medio ciclo.

\[i_C = k \frac{V_{CEQ}}{r_L} \sin 2 \pi ft \label{9.6} \]

\[v_{CE} = V_{CEQ} (1−k \sin 2 \pi ft) \label{9.7} \]

Dónde\(0 \leq k \leq 1\)

Para mayor comodidad, estableceremos\(2 \pi f\) en 1. Para obtener la disipación de potencia, encontramos el producto de la corriente y voltaje del transistor.

\[P_D = i_C v_{CE} \nonumber \]

\[P_D = k \frac{V_{CEQ}}{r_L} \sin t \times V_{CEQ} (1−k \sin t) \nonumber \]

\[P_D = \frac{{V_{CEQ}}^2}{r_L} k \sin t− \frac{{V_{CEQ}}^2}{r_L} k^2 \sin^2 t \nonumber \]

\[P_D = \frac{{V_{CEQ}}^2}{r_L} (k \sin t −k^2 \sin^2 t) \nonumber \]

Eliminar\(\sin^2\) término feo...

\[P_D = \frac{{V_{CEQ}}^2}{r_L} \left( k \sin t + \frac{k^2}{2} \cos 2t − \frac{k^2}{2} \right) \nonumber \]

.. e integrar para obtener:

\[P_D = \frac{{V_{CEQ}}^2}{r_L} \left(−k \cos t − \frac{k^2}{4} \sin 2t − \frac{k^2 t}{2} \right) |_0^\pi \nonumber \]

Tenga en cuenta que\(\frac{V_{CEQ}^2}{r_L} = 2 P_{load (max)}\) Esta es una constante, así que reemplázala para simplificar y luego evaluar la expresión. Por último, divídalo\(2 \pi\) para encontrar el promedio a lo largo de un ciclo completo.

\[P_D = \frac{2 P_{load (max)} \left( 2k − \frac{k^2 \pi}{2} − \frac{k^2 t}{2} \right)}{2 \pi} \\ P_D = 2 P_{load (max)} \left( \frac{k}{\pi} − \frac{k^2}{4} \right) \label{9.8} \]

La ecuación\ ref {9.8} es el caso general. Para el peor de los casos, necesitamos el\(k\) valor mínimo/máximo. Tomaremos la derivada de Ecuación\ ref {9.8} y luego la pondremos a cero para encontrar el peor valor de caso de\(k\).

\[P_D = 2 P_{load (max )} \left( \frac{k}{\pi} − \frac{k^2}{4} \right) \nonumber \]

\[\frac{d P_D}{d k} = 2 P_{load (max)} \left( \frac{1}{\pi} − \frac{k}{2} \right) \nonumber \]

El peor de los casos ocurre en\(k = 2/ \pi \). Esto significa que solo\(2/ \pi \), o 63.7%, de la línea de carga se usa al calentamiento máximo del transistor. 63.7% de la línea de carga corresponde a una potencia de carga de aproximadamente 40% de\(P_{load(max)}\) (i.e.,\(0.637^2\)). Ahora sustituimos este valor por la Ecuación\ ref {9.8} para encontrar el peor de los casos\(P_D\).

\[P_D = 2 P_{load (max)} \left( \frac{2/ \pi}{\pi} − \frac{(2/ \pi )^2}{4} \right) \\ P_D = \frac{2}{\pi^2} P_{load (max )} \approx \frac{ P_{load (max)}}{5} \label{9.9} \]

El resultado final es que cuando la carga está recibiendo alrededor del 40% de su potencia máxima, los transistores estarán en su punto más caliente y estarán disipando aproximadamente 20% de la potencia máxima de carga (o aproximadamente la mitad de la potencia entregada a la carga en ese punto). Por lo tanto, si un amplificador de clase B está clasificado para producir una potencia de carga máxima de 100 vatios, los transistores se calentarán cuando la carga esté recibiendo 40 vatios, y cada transistor estará disipando 20 vatios. Los transistores estarán disipando menos potencia cuando la carga esté al máximo. Esto se verifica fácilmente sustituyendo\(k = 1\) en la Ecuación\ ref {9.8}. El resultado es una disipación de potencia de 13.7% de la potencia de carga máxima, o 13.7 vatios para el ejemplo anterior.

Para ayudar a obtener una comprensión más profunda de precisamente lo que está sucediendo aquí, las formas de onda del transistor se trazan en Figuras\(\PageIndex{10}\) y\(\PageIndex{11}\). El caso de potencia de carga máxima se presenta en la Figura\(\PageIndex{10}\). Aquí, vemos el lleno\(i_C\) y\(v_{CE}\) columpios. Tenga en cuenta que cuando\(i_C\) es máximo,\(v_{CE}\) es 0, de ahí que la potencia sea 0. En contraste, la Figura\(\PageIndex{11}\) muestra el peor de los casos. La corriente del colector alcanza un pico de poco menos del 64% del máximo, pero\(v_{CE}\) cae a solo aproximadamente 36% en lugar de 0% de su máximo. Esto da como resultado una curva de disipación de potencia con un área considerablemente mayor por debajo de ella, lo que indica una mayor potencia promedio.

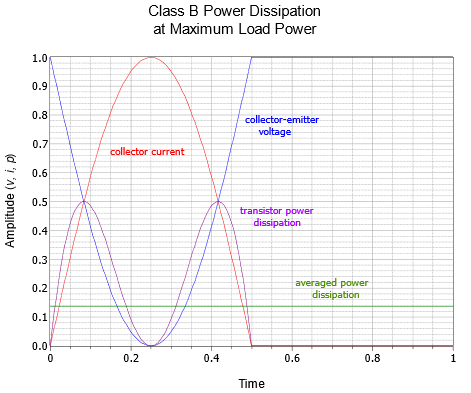
Figura\(\PageIndex{10}\): Disipación de potencia del transistor Clase B en\(P_{Load(max)}\).

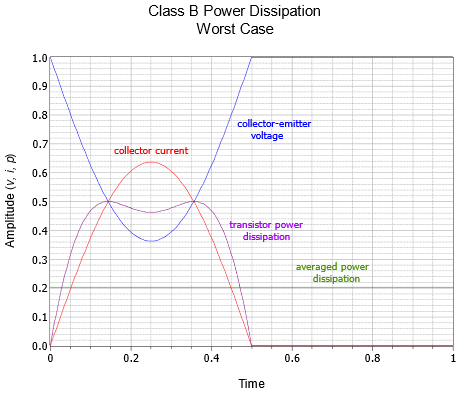
Figura\(\PageIndex{11}\): Disipación de potencia del transistor Clase B, peor de los casos.

Por último, vale la pena recordar que los problemas de carga reactiva discutidos para los amplificadores de clase A aún se aplican a los amplificadores de clase B. Las cargas con una impedancia compleja pueden ser más difíciles de manejar que las cargas puramente resistivas ideales examinadas aquí. Por lo tanto, es posible que tengamos que sobrevalorar los transistores anteriores\(P_{load(max)} /5\). Como nota al margen, la línea de carga de CA para un amplificador de clase B con carga reactiva aparecerá como una elipse que se ha cortado por la mitad (refiérase de nuevo a la Figura 8.4.5 e imagine una línea de corte horizontal que recorre el punto Q).

9.2.5: Eficiencia Clase B

La eficiencia se define como potencia útil de salida o carga frente a la alimentación de CC suministrada.

\[\eta = \frac{P_{out}}{P_{i n}} = \frac{P_{load (max )}}{P_{DC}} \nonumber \]

Esto es dinámico para amplificadores de clase B. En\(P_{load(max)}\) la fuente de CC está entregando el voltaje completo de\(2 V_{CEQ}\) y el valor pico correspondiente de la corriente es\(i_{C(sat)}\).

\[i_{C(sat )} = \frac{V_{CEQ}}{r_L} \nonumber \]

El promedio de esto a lo largo de un medio ciclo es

\[i_{C(avg )} = \frac{1}{\pi} \times \frac{V_{CEQ}}{r_L} \nonumber \]

Por lo tanto, la alimentación suministrada debe ser

\[P_{DC} = 2V_{CEQ} i_{C(sat)} \nonumber \]

\[P_{DC} = 2V_{CEQ} \times \frac{1}{\pi} \frac{V_{CEQ}}{r_L} \nonumber \]

\[P_{DC} = \frac{2}{\pi} \times \frac{{V_{CEQ}}^2}{r_L} \nonumber \]

Como se señaló anteriormente V CEQ 2 r L = 2 Cargar (máx) por lo tanto

\[P_{DC} = \frac{4}{\pi} \times P_{load (max)} \nonumber \]

Finalmente, sustituya esta expresión de nuevo en la definición original por eficiencia.

\[\eta_{max} = \frac{P_{load (max)}{{P_{DC}} \nonumber \]

\[\eta_{max} = \frac{P_{load (max)}}{\frac{4}{\pi} P_{load (max)}} \nonumber \]

\[\eta_{max} = \frac{\pi}{4} \nonumber \]

\[\eta_{max} \approx 78.5\% \nonumber \]

Encontramos que la máxima eficiencia teórica de un amplificador de clase B es más de tres veces mayor que la de un amplificador de clase A.

Tiempo para un ejemplo.

Ejemplo\(\PageIndex{1}\)

El amplificador mostrado en la Figura\(\PageIndex{12}\) está accionando un\( \Omega \) altavoz nominal 8. Determine el cumplimiento, la potencia de carga máxima y la disipación de transistores en el peor También estime\(Z_{in}\) asumiendo\(\beta = 50\) y determine las clasificaciones de transistores para la corriente máxima y\(BV_{CEO}\).

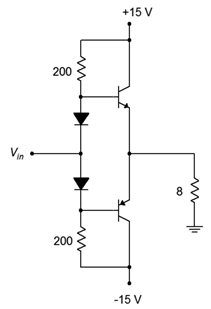
Figura\(\PageIndex{12}\): Esquema por ejemplo\(\PageIndex{1}\).

Por inspección,\(V_{CEQ} = 15\) V. Este es el cumplimiento máximo.

\[compliance = 15 V peak = 10.6 V RMS \nonumber \]

Dado el cumplimiento, podemos usar la ley de energía para encontrar la potencia de carga

\[P_{load (max)} = \frac{{Compliance_{RMS}}^2}{R_L} \nonumber \]

\[P_{load (max)} = \frac{(0.707 \times 15V)^2}{8 \Omega } \nonumber \]

\[P_{load (max)} = 14W \nonumber \]

Eso no es enorme pero podría ser suficiente para irritar a los vecinos.

La disipación de potencia en el peor caso de los transistores es

\[P_D = \frac{P_{load (max)}}{5} \nonumber \]

\[P_D = \frac{14W}{5} \nonumber \]

\[P_D = 2.8 W \nonumber \]

El voltaje de ruptura es todo el suministro así\(BV_{CEO} > 30\) V. La corriente máxima a través de los transistores es la misma que la corriente de carga máxima o\(i_{C(sat)}\).

\[i_{C(sat )} = \frac{V_{CEQ}}{r_L} \nonumber \]

\[i_{C(sat )} = \frac{15 V}{8 \Omega} \nonumber \]

\[i_{C(sat )} = 1.88 A \nonumber \]

La impedancia de entrada se encuentra de la manera habitual pero con un giro menor. \(Z_{in(base)}\)es aproximadamente igual a\(\beta r_L\), o alrededor de 400\( \Omega \). Sin embargo, solo un transistor está encendido en un momento dado, así que esto está en paralelo con las dos 200 resistencias de\( \Omega \) polarización pero no con la otra\(Z_{in(base)}\) (el transistor “off” tiene una impedancia de entrada muy alta porque no está conduciendo). Esto deja una impedancia\(Z_{in(base)}\) de aproximadamente 80\( \Omega \), o diez veces la carga.

Simulación por Computadora

Para verificar el funcionamiento básico de un amplificador de clase B, el circuito de la Figura\(\PageIndex{13}\) se introduce en un simulador. El amplificador debe sujetarse justo debajo de los rieles de alimentación de\(\pm\) 10 voltios para que se use una fuente de pico de 10 voltios para verificar esto. Además,\(A_v\) debe ser de aproximadamente 1.

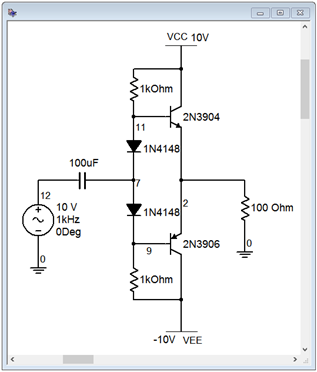
Figura\(\PageIndex{13}\): Amplificador Clase B en simulador.

Los resultados de un análisis transitorio se muestran en la Figura\(\PageIndex{14}\). Primero, es evidente que la ganancia de voltaje es aproximadamente la unidad ya que las ondas de entrada y salida son casi coincidentes (con la excepción de la porción recortada). El recorte ocurre a aproximadamente 8.5 voltios. Esto se debe en gran parte a la limitación de los diodos de polarización. Una vez que la entrada se acerca en valor a la fuente de alimentación, los diodos se polarizan hacia atrás y la señal no llega a la base. Así, la salida se acorta prematuramente.

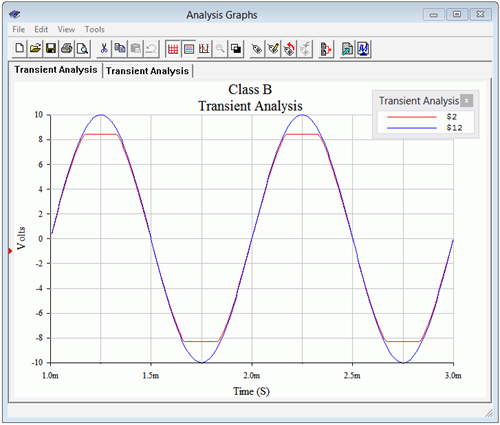
Figura\(\PageIndex{14}\): Análisis transitorio de amplificador de clase B.

Para verificar comentarios anteriores con respecto a los diodos de polarización, el circuito se modifica para que los diodos se cortocircuiten y se vuelva a ejecutar el análisis transitorio. Los resultados se muestran en la Figura\(\PageIndex{15}\).

Dos cosas deberían ser evidentes en la nueva simulación. Primero, la forma de onda de salida está sufriendo una distorsión de muesca obvia. Por lo tanto, podemos estar contentos de que los diodos de polarización hayan hecho su trabajo para reducir este efecto. El segundo ítem involucra el cumplimiento. La nueva salida no está recortada. Por supuesto, la falta de diodos de polarización ha reducido la señal en aproximadamente 0.7 voltios, pero un examen cuidadoso de la forma de onda de salida muestra que ha alcanzado más de 9 voltios pico sin recorte. De hecho, si aumentamos la entrada a 12 voltios pico, como en la Figura\(\PageIndex{16}\), podemos ver que el recorte se produce justo debajo de los rieles de alimentación. Así, el recorte prematuro se debe a los diodos y a su interacción con las fuentes de alimentación y las resistencias circundantes. En resumen, perdemos un poco de cumplimiento debido a los diodos pero eso es mucho mejor que obtener distorsión de notch.

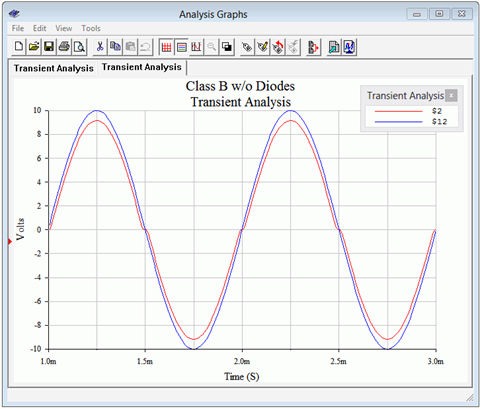
Figura\(\PageIndex{15}\): Análisis transitorio de amplificador Clase B, sin diodos de polarización.

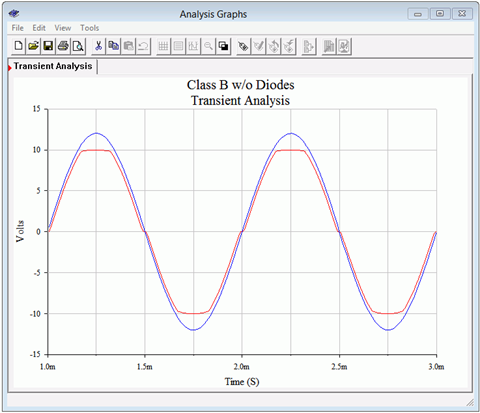
Figura\(\PageIndex{16}\): Análisis transitorio de amplificador Clase B, sin diodos de polarización y mostrando recorte.

9.2.6: Conductor de acoplamiento directo

Los circuitos que hemos examinado ofrecen tanto ganancia de corriente como ganancia de potencia, pero no ganancia de voltaje. Para aumentar el voltaje de la señal, lo más probable es que se necesiten algunas etapas de ganancia de voltaje anteriores. Estas etapas se pueden conectar a los circuitos seguidores de clase B anteriores con condensadores de acoplamiento, pero este no es el método más efectivo. Una técnica más común es el uso de un controlador de acoplamiento directo.

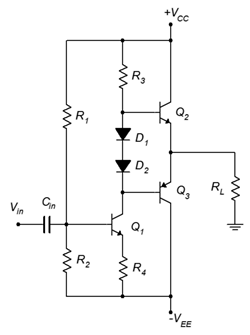
Figura\(\PageIndex{17}\): Amplificador Clase B con controlador de acoplamiento directo.

Un seguidor de clase B con una etapa de accionamiento acoplado directo se muestra en la Figura\(\PageIndex{17}\). Lo que hemos hecho aquí es combinar un amplificador emisor común de clase A ordinario (en este caso, usando polarización de divisor de voltaje) con un seguidor de clase B. El seguidor se posiciona donde la resistencia de colector de la etapa de emisor común estaría normalmente. Esto elimina tres componentes: la resistencia de colector, el condensador de acoplamiento entre etapas y la resistencia de polarización de base inferior de la etapa de salida de clase B. La eliminación de las resistencias eleva la resistencia de carga efectiva para la primera etapa, produciendo así una mayor ganancia de voltaje desde la etapa del controlador.

Desviar el controlador de acoplamiento directo no es difícil si recordamos una cosa: el voltaje de CC\(R_3\) debe ser igual a aproximadamente\(V_{CC} − 0.7\) V. Si este no es el caso, la etapa de clase B no será simétrica, o en otras palabras\(V_{CEQ2} \neq V_{CEQ3}\), y la salida final no estará asentada a 0 VDC ya que necesita. Conociendo el valor de\(R_3\) y su voltaje, podemos determinar su corriente. Esta corriente fluye hacia abajo en\(Q_1\) as\(I_{CQ1}\). Sabiendo\(I_{CQ1}\), podemos determinar el voltaje a través\(R_4\) y eventualmente determinar la relación de divisor adecuada para\(R_1\) y\(R_2\) para lograr este valor.

Ejemplo\(\PageIndex{2}\)

Usando el amplificador de dos etapas de la Figura\(\PageIndex{17}\), primero determine los valores para\(R_1\) y\(R_2\) para obtener el sesgo adecuado del sistema. Determine el cumplimiento de la salida, la potencia de carga máxima y la disipación del transistor en el peor También estimar\(A_v\). Asumir\(\beta = 50\) para los dispositivos de salida y 100 para la primera etapa. \(V_{CC} = 20\)V,\(V_{EE} = −20\) V,\(R_L = 16\)\( \Omega \),\(R_3 = 560\)\( \Omega \),\(R_4 = 75\)\( \Omega \).

Para la sección de salida (suponiendo que esté sesgada adecuadamente), por inspección,\(V_{CEQ} = 20\) V. Esta es la máxima conformidad.

\[compliance = 20 V peak = 14.1 V RMS \nonumber \]

Dado el cumplimiento, podemos usar la ley de energía para encontrar la potencia de carga

\[P_{load (max)} = \frac{{Compliance_{RMS}}^2}{R_L} \nonumber \]

\[P_{load (max)} = \frac{(14.1 V)^2}{16 \Omega} \nonumber \]

\[P_{load (max)} = 12.5 W \nonumber \]

La disipación de potencia en el peor caso de los transistores es

\[P_D = \frac{P_{load (max)}{5} \nonumber \]

\[P_D = \frac{12.5W}{5} \nonumber \]

\[P_D = 2.5 W \nonumber \]

Para determinar las resistencias de polarización, comenzamos con\(R_3\). Para lograr simetría de polarización, todas las\(V_{CC}\) caídas a través\(R_3\) con la excepción de 0.7 voltios para\(D_1\). Esto es lo mismo que\(I_{CQ1}\).

\[I_{CQ_1} = \frac{V_{CC} −0.7V}{R_3} \nonumber \]

\[I_{CQ_1} = \frac{19.3V}{560 \Omega} \nonumber \]

\[I_{CQ_1} = 34.5 mA \nonumber \]

La caída en R4 se encuentra a través de la ley de Ohm

\[V_{R_4} = I_{CQ_1} R_4 \nonumber \]

\[V_{R_4} = 34.5 mA \times 75 \Omega \nonumber \]

\[V_{R_4} = 2.6 V \nonumber \]

Esto implica que el voltaje transversal\(R_2\) debe ser 0.7 voltios más, o 3.3 voltios. Si ignoramos la corriente base de\(Q_1\), entonces la relación de\(R_1\) a\(R_2\) debe ser la misma que la relación de sus voltajes, 36.7 a 3.3, o 11.1 a 1. En otras palabras,\(R_1\) debe ser 11.1 veces mayor que\(R_2\). Para una buena estabilidad al sesgo no deseamos establecer\(R_2\) demasiado más grande que\(R_4\). Si lo establecemos en 200\( \Omega \), por ejemplo, entonces\(R_1\) tendría que ser de aproximadamente 2.2 k\( \Omega \). Debido a las tolerancias de los componentes, una de estas resistencias tendría que ser un potenciómetro (conectado como reóstato) para “ajustar” la salida final a 0 VCC. Un combo resistor/olla podría ser aún mejor ya que no será tan “delicada”. Por ejemplo, los 2.2 k\( \Omega \) podrían ser reemplazados por una combinación en serie de un pote de 1.8 k\( \Omega \) y un\( \Omega \) bote de 1 k. Esto sería mucho más fácil de ajustar que si la resistencia fuera reemplazada por una\( \Omega \) olla estándar de 5 k.

Ahora para la ganancia de voltaje del sistema. La ganancia del seguidor es aproximadamente una por lo que solo necesitamos preocuparnos por el amplificador emisor común de primera etapa. Este amplificador es inundado por\(R_4\) y dado que la corriente del colector es superior a 34 mA,\(r'_e\) será menor que un ohm y puede ser ignorada. Todo lo que tenemos que hacer es encontrar la carga efectiva en el colector de\(Q_1\). Esto es\(R_3\) en paralelo con un solo\(Z_{in(base)}\) (recuerde que solo un transistor está encendido en un momento dado y el transistor de apagado aparecerá como una impedancia alta).

\[Z_{i n(base)} = \beta r_E \nonumber \]

\[Z_{i n(base)} = 100 \times 75 \Omega \nonumber \]

\[Z_{i n(base)} = 7500 \Omega \nonumber \]

\[A_v =− \frac{r_L}{r_E} \nonumber \]

\[A_v =− \frac{7500 \Omega || 560 \Omega}{ 75 \Omega} \nonumber \]

\[A_v =−6.95 \nonumber \]

Antes de salir de esta sección, hay algunos elementos a tener en cuenta. En primer lugar, los cálculos de potencia de carga han supuesto que toda la fuente de alimentación puede ser utilizada por los dispositivos de salida. Como vimos con la versión de polarización de diodos, este no siempre es el caso. Hay otra situación que puede limitar el swing de salida. La etapa de clase B es un seguidor y por lo tanto tiene una ganancia de voltaje de uno. Si la etapa del conductor no puede producir el swing completo, entonces la etapa de salida tampoco puede. En consecuencia, se necesita realizar un análisis de clase A (es decir, línea de carga de CA) en el controlador para determinar qué tan grande puede ser la señal antes de recortar. De hecho, es muy probable que la etapa del conductor se corte antes de la etapa de salida.

Además, el controlador de acoplamiento directo no tiene que ser un NPN como se representa en la Figura\(\PageIndex{17}\). En su lugar se puede usar un PNP, simplemente necesita ser desplazado a la sección superior en lugar de a la sección inferior, como se muestra en la Figura\(\PageIndex{18}\).

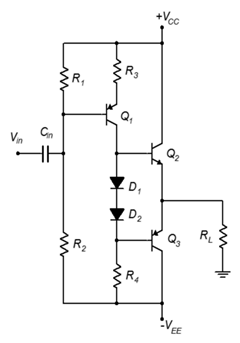
Figura\(\PageIndex{18}\): Amplificador Clase B con controlador de acoplamiento directo, versión PNP.

Referencias

¹ Piensa en un motor de automóvil: ¿Cuánto sentido tendría tener un motor con un máximo de 6000 RPM funcionando a 3000 RPM cuando estás sentado inmóvil en un semáforo en rojo?

² Por supuesto, la resistencia dinámica es una función de la corriente que fluye a través del diodo por lo que fluctuará a medida que cambie la señal. Esto se piensa mejor como un mecanismo generador de distorsión porque alterará ligeramente la señal que llega a la base. Esta distorsión es muy probablemente órdenes de magnitud menor que la distorsión de muesca que mitiga el diodo, por lo que es un buen comercio.