11.3: Amplificador de Fuente Común
- Page ID
- 83467
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El amplificador de fuente común es análogo al amplificador emisor común. El prototipo de circuito amplificador con modelo de dispositivo se muestra en la Figura\(\PageIndex{1}\).
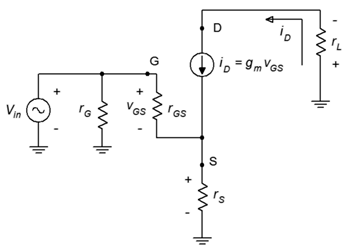
Figura\(\PageIndex{1}\): Amplificador de fuente común con modelo.
Este circuito incluye una resistencia de pantano,\(r_S\). La señal de entrada se presenta al terminal de puerta mientras que la salida se toma del desagüe.
11.3.1: Ganancia de voltaje
Una ecuación para la ganancia de voltaje,\(A_v\), se desarrolla de la siguiente manera. Primero, comenzamos con la definición fundamental, a saber, que la ganancia de voltaje es la relación de\(v_{out}\) a\(v_{in}\), y procedemos expresando estos voltajes en términos de sus equivalentes de ley de Ohm.
\[A_v = \frac{v_{out}}{v_{i n}} = \frac{v_D}{v_G} \\ A_v = \frac{−i_D r_L}{i_D r_S+v_{GS}} \\ A_v = \frac{−g_m v_{GS} r_L}{g_m v_{GS} r_S+v_{GS}} \\ A_v =− \frac{g_m r_L}{g_m r_S+1} \label{11.1} \]
Si no hay resistencia de pantano, la primera porción del denominador cae y la ganancia se simplifica a\(−g_m \cdot r_L\). El resistor de pantano en la fuente\(r_S\),, juega el mismo papel aquí que en el BJT: ayuda a estabilizar la ganancia y reducir la distorsión. Lo hace a expensas de la ganancia de voltaje.
11.3.2: Impedancia de entrada
Refiriéndonos de nuevo a la Figura\(\PageIndex{1}\), la impedancia de entrada del amplificador estará\(r_G\) en paralelo con la impedancia mirando hacia el terminal de puerta,\(Z_{in(gate)}\). Para el caso no inundado, este será\(r_{GS}\). A bajas frecuencias\(r_{GS}\) es muy grande, bien entrado en los megohmios. En la mayoría de los circuitos prácticos,\(r_G\) será mucho menor, de ahí
\[Z_{in} = r_G || r_{GS} \approx r_G \label{11.2} \]
Teóricamente, para los amplificadores inundados\(Z_{in(gate)}\) será mayor que\(r_{GS}\) pero este es un punto discutible. En cualquier caso, es relativamente fácil obtener una impedancia de entrada alta, ciertamente mucho más fácil de lo que es para los amplificadores BJT típicos de un solo dispositivo.
Podría ser fácil volverse complaciente y simplemente asumir que\(r_G\) establece la impedancia de entrada y ese es el final de la misma. Esto sería un error. Como se mencionó anteriormente, con impedancias tan altas, no podemos ignorar elementos como la capacitancia de unión. Por ejemplo, para un dispositivo de propósito general, un valor típico para\(C_{iss}\), la capacitancia de entrada total, puede estar en las proximidades de 5 a 10 pF. Esta capacitancia aparece en paralelo con\(r_G\). Si este amplificador se usa para señales ultrasónicas, la reactancia capacitiva\(X_C\),, sería tan baja como 160 k\(\Omega\) a 100 kHz. Aunque esto es alto en comparación con los circuitos BJT típicos, es menor que los\(R_G\) valores comúnmente utilizados para la polarización. A frecuencias más altas, la situación es aún peor ya que\(X_C\) disminuye con la frecuencia. Además, aquí estamos ignorando el efecto Miller que hace que la situación sea aún peor que incluso peor, así que quizás podamos decir que es aún peor, que es una afirmación que también podríamos hacer con respecto a la gramática de esta oración.
11.3.3: Impedancia de salida
Para investigar la impedancia de salida, nos referiremos a la Figura\(\PageIndex{2}\). Este circuito es muy similar al de la Figura\(\PageIndex{1}\). La principal diferencia es que el equivalente de carga de CA se ha dividido en sus dos componentes, la carga en sí\(R_L\), y la resistencia de polarización de drenaje,\(R_D\).
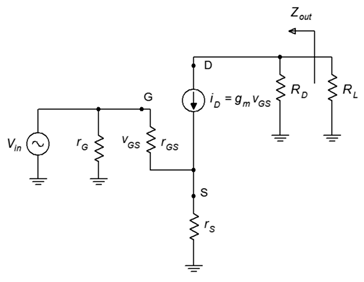
Figura\(\PageIndex{2}\): Impedancia de salida del amplificador de fuente común.
Desde el punto de vista de\(R_L\), mirando de nuevo al amplificador vemos\(R_D\) en paralelo con la impedancia en el drenaje. En el desagüe encontramos la fuente de corriente,\(i_D\). La impedancia interna de esta fuente de corriente equivalente es muy alta en comparación con los valores típicos para\(R_D\) (cientos de k\(\Omega\)), por lo tanto podemos aproximar la impedancia de salida como
\[Z_{out} \approx R_D \label{11.3} \]
Cabe señalar que todas las formas de sesgo DC discutidas en el capítulo anterior son juego aquí. Sin embargo, hay algunas limitaciones a tener en cuenta. Por ejemplo, cuando se usa polarización de voltaje constante, el pantano no es posible ya que esa forma de polarización no usa una resistencia de fuente. Por el contrario, la autopolarización y la polarización combinada incluyen una resistencia de fuente, por lo que el enjambramiento es una posibilidad, sin embargo,\(R_S\) puede necesitar dividirse y desviarse parcialmente para lograr los resultados deseados. Finalmente, la polarización de corriente constante no está bien posicionada para usar el pantano, ya que eso requeriría algún trabajo adicional para encajar en una nueva\(R_S\) junto con la fuente de corriente. Más típicamente, la fuente de corriente simplemente se derivará con un condensador para producir un amplificador no inundado.
Ejemplo\(\PageIndex{1}\)
Determine la ganancia de voltaje y la impedancia de entrada para el circuito mostrado en la Figura\(\PageIndex{3}\). Supongamos\(I_{DSS} = 15\) mA y\(V_{GS(off)} = −3\) V.
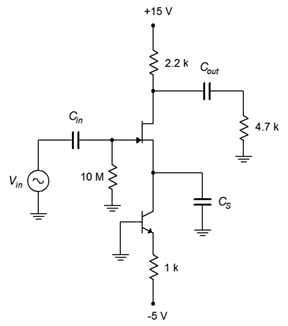
Figura\(\PageIndex{3}\): Circuito por Ejemplo\(\PageIndex{1}\).
Este es un amplificador de fuente común no inundado con polarización de corriente constante. Podemos determinar\(Z_{in}\) a través de la inspección.
\[Z_{i n} = Z_{i n(gate)} || R_G \nonumber \]
\[Z_{i n} \approx 10 M \Omega \nonumber \]
Para encontrar la ganancia de voltaje, primero necesitaremos encontrar\(I_D\) y con\(g_{m0}\) el fin de encontrar\(g_m\).
\[I_D = \frac{∣V_{EE}∣−0.7 V}{R_E} \nonumber \]
\[I_D = \frac{5 V−0.7 V}{1k \Omega} \nonumber \]
\[I_D = 4.3 mA \nonumber \]
\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS (off )}} \nonumber \]
\[g_{m0} =− \frac{30 mA}{−3V} \nonumber \]
\[g_{m0} = 10mS \nonumber \]
Conociendo la transconductancia actual y máxima, podemos encontrar\(g_m\) a través del uso de la Ecuación 10.2.4.
\[\frac{g_m}{g_{m0}} = \sqrt{\frac{I_D}{I_{DSS}}} \nonumber \]
\[g_m = g_{m0} \sqrt{\frac{I_D}{I_{DSS}}} \nonumber \]
\[g_m = 10 mS \sqrt{\frac{4.3mA}{15 mA}} \nonumber \]
\[g_m = 5.35mS \nonumber \]
\[A_v =− \frac{g_m r_L}{g_m r_S+1} \nonumber \]
\[A_v =− \frac{5.35 mS(2.2k \Omega || 4.7 k\Omega)}{5.35mS \times 0 \Omega +1} \nonumber \]
\[A_v =−8.02 \nonumber \]
Ejemplo\(\PageIndex{2}\)
Determine la ganancia de voltaje y la impedancia de entrada para el circuito mostrado en la Figura\(\PageIndex{3}\). Supongamos\(I_{DSS} = 24\) mA y\(V_{GS(off)} = −4\) V.
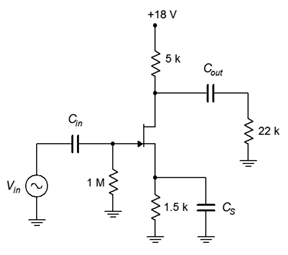
Figura\(\PageIndex{4}\): Circuito por ejemplo\(\PageIndex{2}\)
Este es un amplificador de fuente común sin interrupciones con autopolarización. Una vez más, podemos determinar\(Z_{in}\) vía inspección.
\[Z_{i n} = Z_{i n(gate)} || R_G \nonumber \]
\[Z_{i n} \approx 1 M\Omega \nonumber \]
Para encontrar la ganancia de voltaje, primero necesitaremos encontrar\(g_{m0}\). Además, podemos tomar un atajo y encontrar la corriente de drenaje normalizada del gráfico de autopolarización en lugar de encontrarse a\(I_D\) sí misma.
\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS (off )}} \nonumber \]
\[g_{m0} =− \frac{48 mA}{−4 V} \nonumber \]
\[g_{m0} = 12mS \nonumber \]
\(R_S\)es de 1.5 k\(\Omega\), por lo tanto\(g_{m0}R_S = 18\). A partir de la gráfica de autopolarización esto produce una corriente de drenaje normalizada de 0.08.
\[g_m = g_{m0} \sqrt{\frac{I_D}{I_{DSS}}} \nonumber \]
\[g_m = 12mS\sqrt{0.08} \nonumber \]
\[g_m = 3.4 mS \nonumber \]
Nuevamente, no hay pantanos así\(r_S = 0\). La fórmula de ganancia se reduce a
\[A_v =−g_m r_L \nonumber \]
\[A_v =−3.4mS(22k \Omega || 5k \Omega) \nonumber \]
\[A_v =−13.9 \nonumber \]
Ahora volveremos nuestra atención al efecto de los pantanos. Al igual que en el caso BJT, esperamos sacrificar la ganancia y a cambio, ver una mejora en la distorsión. Esto lo examinaremos mediante el uso de una simulación.
Simulación por Computadora
Un amplificador de fuente común que utiliza autopolarización se introduce en el simulador como se muestra en la Figura\(\PageIndex{5}\).
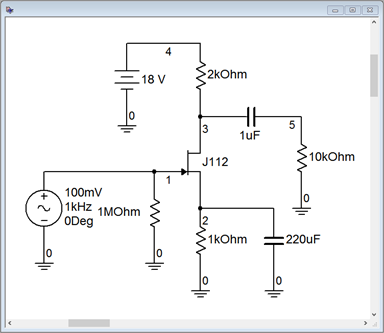
Figura\(\PageIndex{5}\): Amplificador de fuente común en simulador.
Los valores razonables del dispositivo para este modelo son\(I_{DSS} = 40\) mA y\(V_{GS(off)} = −2.3\) V. Basándonos en estos encontramos
\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS(off )}} \nonumber \]
\[g_{m0} =− \frac{80 mA}{−2.3V} \nonumber \]
\[g_{m0} = 34.8mS \nonumber \]
Dada\(R_S = 1\) k\(\Omega\), la ecuación de autosesgo rinde
\[I_D = 2 I_{DSS} \left( \frac{1+g_{m0} R_S − \sqrt{1+2 g_{m0} R_S}}{( g_{m0} R_S )^2} \right) \nonumber \]
\[I_D = 2 I_{DSS} \left( \frac{1+34.8 −\sqrt{1+2 \times 34.8}}{(34.8)^2} \right) \nonumber \]
\[I_D = 1.81mA \nonumber \]
\[g_m = g_{m0} \sqrt{\frac{I_D}{I_{DSS}}} \nonumber \]
\[g_m = 34.8mS \sqrt{\frac{1.81 mA}{40 mA}} \nonumber \]
\[g_m = 7.4 mS \nonumber \]
\[A_v =−g_m r_L \nonumber \]
\[A_v =−7.4mS(2k \Omega || 10k \Omega) \nonumber \]
\[A_v =−12.3 \nonumber \]
Los resultados de un análisis transitorio se muestran en la Figura\(\PageIndex{6}\) para una señal de entrada de pico de 100 mV.
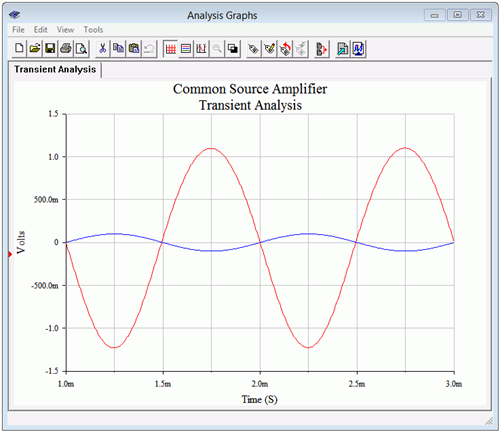
Figura\(\PageIndex{6}\): Análisis transitorio del amplificador de fuente común.
Primero, la inversión entre la entrada (traza azul) y la salida (traza roja) es obvia. Además, cierta distorsión es evidente en la forma de onda de salida. Inspeccionar los picos positivos y negativos muestra que los picos positivos son un poco más amplios que los negativos y no alcanzan la misma magnitud. La ganancia promedio es de aproximadamente −11.75, alrededor de 5% baja de la estimación y no muy mal considerando la distorsión.
La simulación se ejecuta por segunda vez, pero esta vez alrededor de la resistencia de\(\Omega\) fuente de 1 k se divide en un\(\Omega\) par\(\Omega\) 200/800 con solo el 800\(\Omega\) siendo desviado. La polarización de CC no cambia dejando\(g_m\) intacta, pero la nueva resistencia de\(\Omega\) enjambre 200 reduce la ganancia a
\[A_v =− \frac{g_m r_L}{g_m r_S+1} \nonumber \]
\[A_v =− \frac{7.4 mS(2 k \Omega || 10 k \Omega)}{7.4mS \times 200 \Omega +1} \nonumber \]
\[A_v =−4.96 \nonumber \]
La señal de salida del simulador se muestra en la Figura\(\PageIndex{6}\).
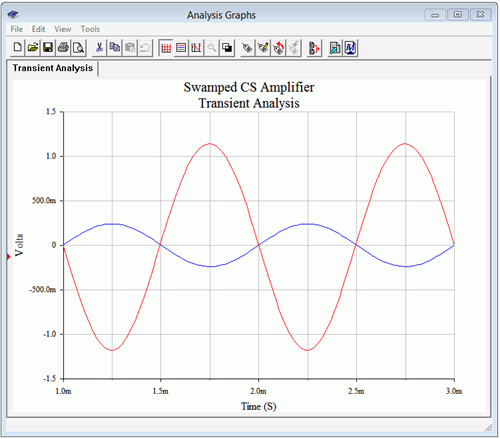
Figura\(\PageIndex{7}\): Análisis transitorio del amplificador de fuente común inundado.
La señal de entrada se elevó a 240 mV pico con el fin de mantener las señales de salida de las dos versiones en la misma amplitud. La simetría parece ser mejor aquí y la ganancia llega a −4.85, solo unos pocos por ciento baja.
A continuación se realiza el análisis de distorsión armónica total (THD). Los resultados se muestran en las Figuras\(\PageIndex{8}\) y\(\PageIndex{9}\). Para mantener la comparación justa, los niveles de entrada se ajustan para mantener voltajes de salida similares. Los resultados no inundados se ven en la Figura\(\PageIndex{8}\), y como se esperaba con base en la asimetría de la forma de onda, el THD es relativamente alto en aproximadamente 4%. La versión inundada obtiene mejores puntajes con poco más de 1.6%, aunque esto todavía no es un rendimiento estelar.
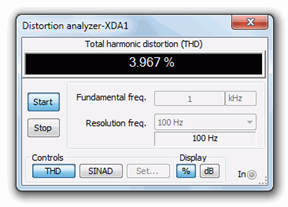
Figura\(\PageIndex{8}\): THD de amplificador de fuente común.
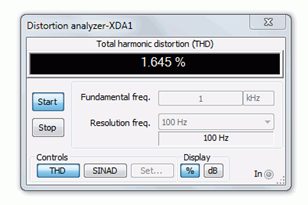
Figura\(\PageIndex{9}\): THD del amplificador de fuente común inundado.
Es interesante señalar que si bien la ganancia de voltaje del amplificador inundado ha caído al 41% de la ganancia no inundada, el THD ha caído al 41% del THD no inundado. De hecho, dada la naturaleza de ley cuadrada de la curva característica, esperaríamos que la distorsión fuera menor si usáramos señales más pequeñas. Para verificar esto, la simulación THD se ejecuta nuevamente para el amplificador inundado, pero ahora usando una señal de entrada diez veces más pequeña a solo 24 mV pico. El resultado se muestra en la Figura\(\PageIndex{10}\).
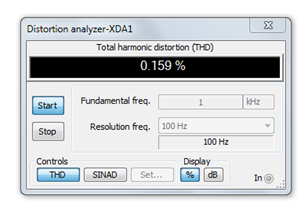
Figura\(\PageIndex{10}\): THD de amplificador de fuente común inundado con nivel de señal reducido.
El THD resultante es marcadamente menor para una mejora de orden de magnitud. Ahora nos estamos acercando al menos al territorio “hi-fi”.


