6.2: Guía de ondas de placa paralela- Introducción
- Page ID
- 83718
Una guía de ondas de placa paralela es un dispositivo para guiar la propagación de ondas entre dos placas perfectamente conductoras. Nuestro interés principal en esta estructura es como un modelo rudimentario aplicable a una amplia gama de problemas de ingeniería. Ejemplos de tales problemas incluyen el análisis de los campos dentro de la línea de microcinta y la propagación de ondas de radio en la ionosfera.
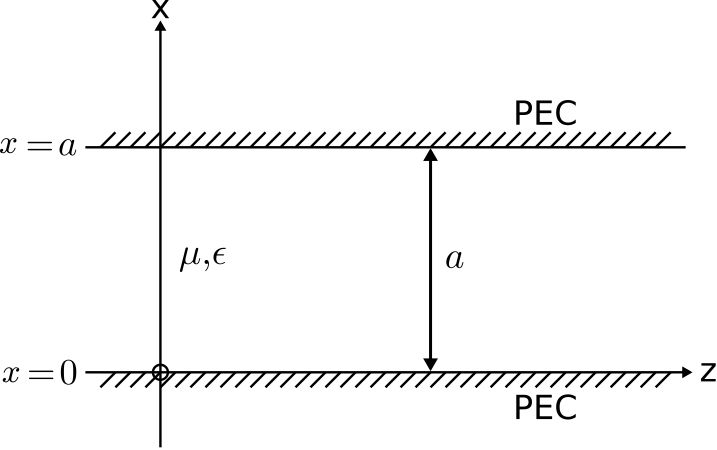
La figura\(\PageIndex{1}\) muestra la geometría de interés. Aquí las placas se encuentran en\(z=0\) y\(z=a\). Se supone que las placas son infinitas en extensión, y por lo tanto no hay necesidad de considerar campos en las regiones\(z<0\) o\(z>a\). Para este análisis, se supone que la región entre las placas consiste en un material ideal (sin pérdidas) que exhibe permeabilidad de valor real\(\mu\) y permitividad de valor real\(\epsilon\).
Limitemos nuestra atención a una región dentro de la guía de ondas que está libre de fuentes. Expresado en forma de fasor, la intensidad del campo eléctrico se rige por la ecuación de onda
\[\nabla^2 \widetilde{\bf E} + \beta^2 \widetilde{\bf E} = 0 \label{m0173_eWE} \]
donde
\[\beta = \omega \sqrt{\mu \epsilon} \nonumber \]
La ecuación\ ref {M0173_EWE} es una ecuación diferencial parcial. Esta ecuación, combinada con las condiciones límite impuestas por las placas perfectamente conductoras, es suficiente para determinar una solución única. Esto se hace más fácilmente en coordenadas cartesianas, como ahora demostraremos. Primero expresamos\(\widetilde{\bf E}\) en coordenadas cartesianas:
\[\widetilde{\bf E} = \hat{\bf x}\widetilde{E}_x + \hat{\bf y}\widetilde{E}_y + \hat{\bf z}\widetilde{E}_z \label{m0173_eE} \]
Esto facilita la descomposición de la Ecuación\ ref {M0173_EWE} en ecuaciones separadas que gobiernan los\(\hat{\bf z}\) componentes\(\hat{\bf x}\)\(\hat{\bf y}\),, de\(\widetilde{\bf E}\):
\[\begin{align} \nabla^2 \widetilde{E}_x + \beta^2 \widetilde{E}_x &= 0 \\ \nabla^2 \widetilde{E}_y + \beta^2 \widetilde{E}_y &= 0 \\ \nabla^2 \widetilde{E}_z + \beta^2 \widetilde{E}_z &= 0 \end{align} \nonumber \]
A continuación observamos que el operador\(\nabla^2\) puede expresarse en coordenadas cartesianas de la siguiente manera:
\[\nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \nonumber \]
por lo que las ecuaciones que rigen los componentes cartesianos de\(\widetilde{\bf E}\) pueden escribirse de la siguiente manera:
\[\begin{align} \frac{\partial^2}{\partial x^2}\widetilde{E}_x + \frac{\partial^2}{\partial y^2}\widetilde{E}_x + \frac{\partial^2}{\partial z^2}\widetilde{E}_x &= - \beta^2 \widetilde{E}_x \label{m0173_eEfx} \\ \frac{\partial^2}{\partial x^2}\widetilde{E}_y + \frac{\partial^2}{\partial y^2}\widetilde{E}_y + \frac{\partial^2}{\partial z^2}\widetilde{E}_y &= - \beta^2 \widetilde{E}_y \label{m0173_eEfy} \\ \frac{\partial^2}{\partial x^2}\widetilde{E}_z + \frac{\partial^2}{\partial y^2}\widetilde{E}_z + \frac{\partial^2}{\partial z^2}\widetilde{E}_z &= - \beta^2 \widetilde{E}_z \label{m0173_eEfz} \end{align} \]
Limitemos nuestra atención a escenarios que pueden describirse completamente en dos dimensiones; a saber\(z\),\(x\) y, y para los cuales no hay variación en\(y\). Esto no se requiere necesariamente, sin embargo, es representativo de una amplia clase de problemas relevantes, y permite simplificar considerablemente las Ecuaciones\ ref {M0173_EEFx} -\ ref {M0173_EEFz}. Si no hay variación en\(y\), entonces las derivadas parciales con respecto a\(y\) son cero, produciendo:
\[\begin{align} \frac{\partial^2}{\partial x^2}\widetilde{E}_x + \frac{\partial^2}{\partial z^2}\widetilde{E}_x &= - \beta^2 \widetilde{E}_x \label{m0173_eEfx2} \\ \frac{\partial^2}{\partial x^2}\widetilde{E}_y + \frac{\partial^2}{\partial z^2}\widetilde{E}_y &= - \beta^2 \widetilde{E}_y \label{m0173_eEfy2} \\ \frac{\partial^2}{\partial x^2}\widetilde{E}_z + \frac{\partial^2}{\partial z^2}\widetilde{E}_z &= - \beta^2 \widetilde{E}_z \label{m0173_eEfz2} \end{align} \]
La solución al problema de la guía de ondas de placa paralela ahora puede resumirse de la siguiente manera: El campo eléctrico\(\widetilde{\bf E}\) (Ecuación\ ref {M0173_EE}) es la solución a Ecuaciones simultáneas\ ref {M0173_EEFx2} -\ ref {M0173_EEFz2} sujeto a las condiciones de límite que se aplican en las superficies PEC en\(z=0\) y \(z=d\); es decir, que la componente tangente de\(\widetilde{\bf E}\) es cero en estas superficies.
En este punto, el problema se ha reducido a un ejercicio rutinario en la solución de ecuaciones diferenciales parciales. Sin embargo, un enfoque algo más útil es descomponer primero el campo eléctrico total en componentes eléctricos transversales (TE) y magnéticos transversales (TM), 1 y determinar las soluciones a estos componentes por separado. El componente TE del campo eléctrico es paralelo a las placas, y por lo tanto transversal (perpendicular) al plano mostrado en la Figura\(\PageIndex{1}\). Así, el componente TE tiene\(\widetilde{E}_x=\widetilde{E}_z=0\), y solo\(\widetilde{E}_y\) puede ser distinto de cero. El componente TM de la intensidad del campo magnético (\(\widetilde{\bf H}\)) es paralelo a las placas, y por lo tanto transversal al plano mostrado en la Figura\(\PageIndex{1}\). Así, el componente TM tiene\(\widetilde{H}_x=\widetilde{H}_z=0\), y solo\(\widetilde{H}_y\) puede ser distinto de cero. Como siempre, el campo total es la suma de los componentes TE y TM.
Las soluciones TE y TM se presentan en las Secciones 6.3 (Componente eléctrico de la solución TE), 6.4 (Componente magnético de la solución TE) y 6.5 (Componente eléctrico de la solución TM). El componente magnético de la solución TM se puede determinar a través de una variación directa de los tres casos anteriores, por lo que no se presenta aquí.
La presentación de la solución para los campos en una guía de ondas de placa paralela bajo las condiciones descritas en la sección continúa en la Sección 6.3.
- Para un repaso sobre la descomposición de TE-TM, consulte la Sección 5.5. ↩