10.3: Implementación de una Máquina de Estado
- Page ID
- 82795
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)\(\PageIndex{1}\)Contador Mod 4
Un contador mod (o módulo) 4 es un circuito que cuenta desde 0.. 3. También se le llama contador de 2 bits porque los números de 0.. 3 se pueden representar usando 2 bits (por ejemplo, 00, 01, 10, 11) 9. El estado del contador se representa en 2 bits, y así se almacena en 2 flip-flops (o pestillos). Debido a que los dos flip-flops se combinan para hacer un solo valor, a menudo se les llama registro de 2 bits.
Las transiciones de estado de esta máquina, como contador, son 00->01->10->11->00. La máquina solo cuenta de 0 a 3 y comienza de nuevo. Esto se representa en el siguiente diagrama de estados.
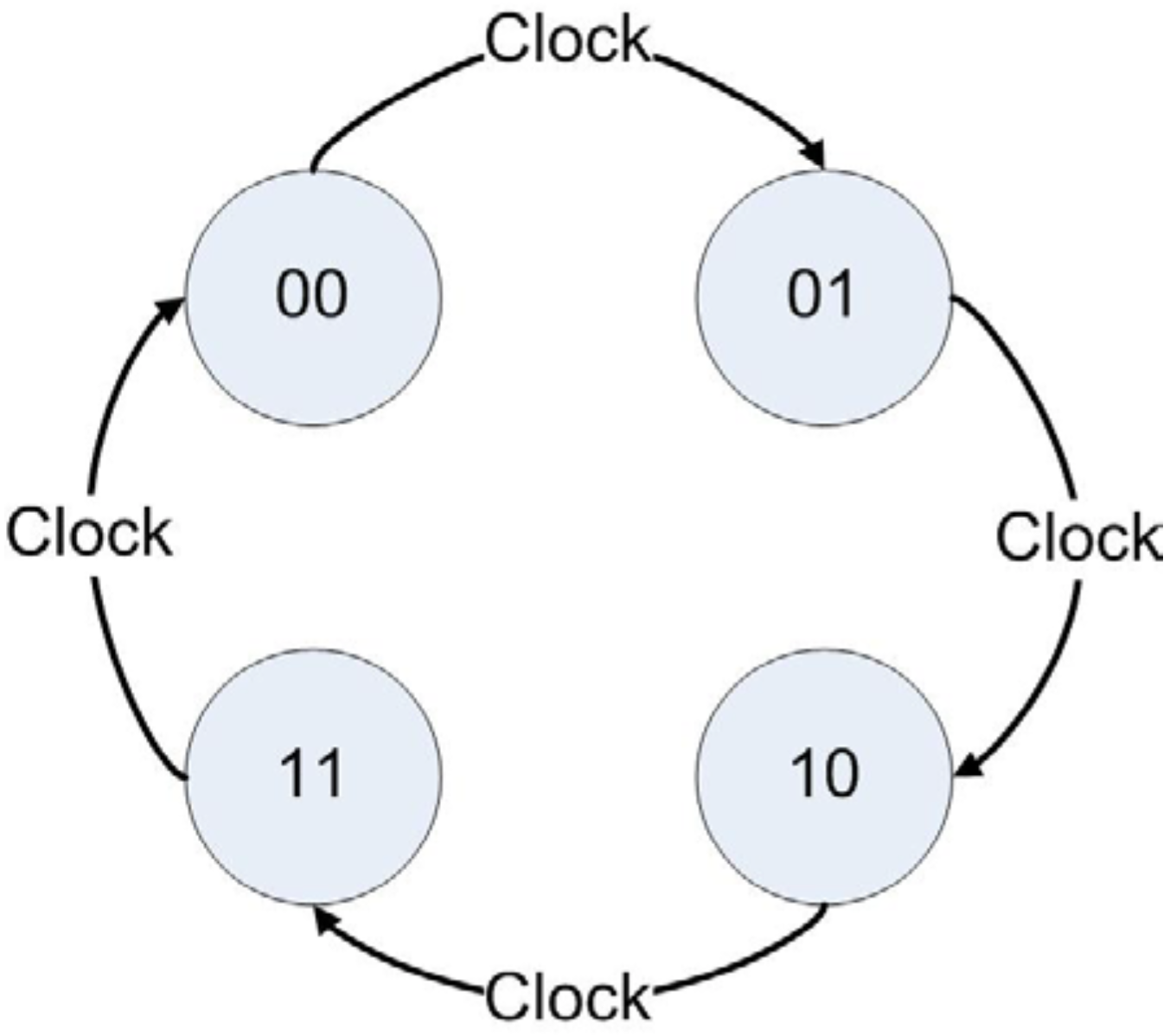
Este diagrama de estados se puede escribir como una tabla de transición de estado, como se muestra a continuación.
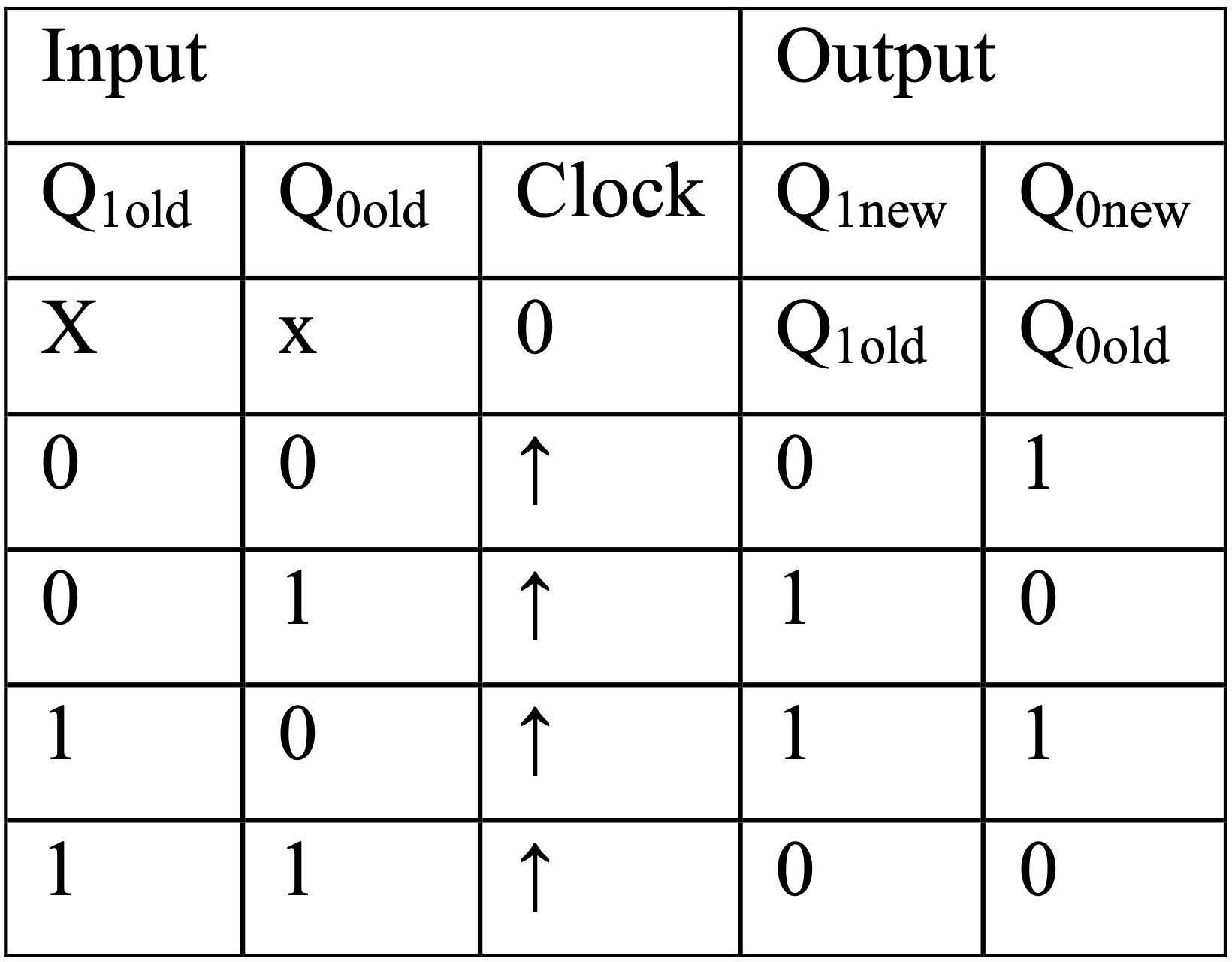
Esta tabla dice que si el reloj no pulsa, Q 1 y Q 0 conservan sus valores antiguos. Cuando el reloj genera un borde ascendente (↑), los valores de Q 1 y Q 0 pasan al siguiente valor en el contador, o su siguiente estado.
\(\PageIndex{2}\)Implementación de un diagrama de transición de estado
La siguiente es una implementación genérica de una máquina de estado. Hay dos componentes. El primero es un registro de n bits, que es una colección de n biestables D de 1 bit o pestillos D. Estos n valores de datos de 1 bit almacenan el estado actual de la máquina y pueden almacenar hasta 2 n estados. El registro cambia de estado cuando el reloj genera un disparador de borde positivo, lo que hace que los flip-flops tomen un nuevo valor.
El registro dará salida a algún conjunto de valores, y al mismo tiempo reciclará su estado de nuevo en un conjunto de puertas que determinarán cómo cambiar el registro al siguiente estado. Este conjunto de puertas se llamará la siguiente lógica de estado. La salida de la siguiente lógica de estado se conectará a la entrada a los registros para que cuando el reloj pulse (o tics), el registro se cargue con los nuevos valores. Esta lógica se representa en la siguiente figura.
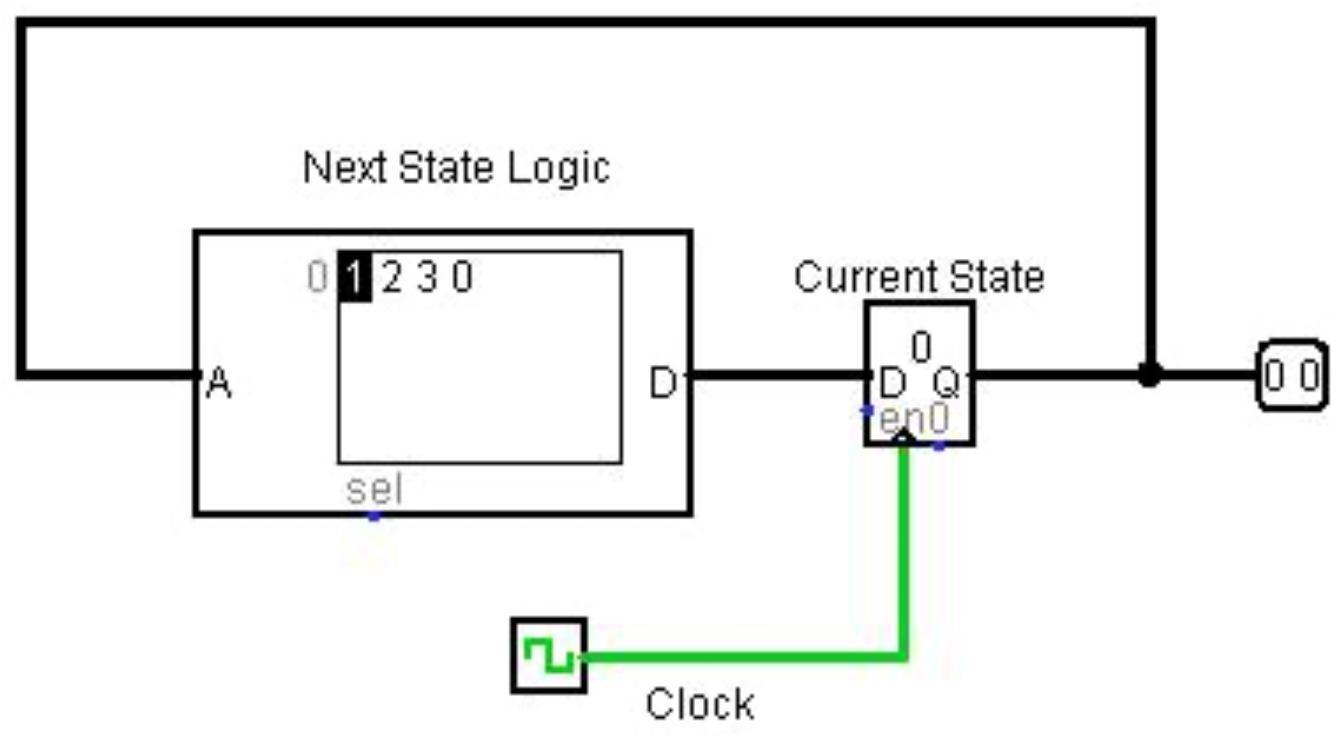
Como este diagrama muestra que la entrada a la siguiente lógica de estado proviene del estado anterior. La lógica del siguiente estado utiliza el estado anterior para calcular el siguiente estado a almacenar en el registro. La marca de reloj hace que el registro almacene un nuevo estado, que se retroalimenta a la lógica de estado siguiente para calcular un nuevo estado siguiente.
Esta visión general explica cómo funciona una máquina de estado, pero ha dejado abierta la cuestión de ¿cómo implementar la siguiente lógica de estado? Hay dos formas básicas de implementar esta lógica, ya sea a través de hardware o usando un micro programa. Una implementación de hardware utiliza puertas para calcular el nuevo estado. Un micro programa se implementa usando la memoria de solo lectura (o ROM), y el siguiente estado se obtiene de una dirección dada por el estado actual. Estos se explicarán en las dos secciones siguientes.
\(\PageIndex{3}\)Implementación de hardware de lógica de siguiente estado
La lógica del siguiente estado debe tomar como entrada el estado actual y convertirlo al siguiente estado. El diagrama de transición de estado en la Figura\(\PageIndex{2}\) es muy similar a una tabla de verdad, donde Q 0old y Q1old son las entradas al circuito, y Q 0new y Q 1new son las salidas. A partir del diagrama de transición de estado, es simple de resolver para las expresiones booleanas, que son Q 0new = (Q 0old '* Q 1old') + (Q 0old '* Q 1old), y Q 1new = (Q 0old XOR Q 1old). El diagrama de circuito para esta lógica de estado siguiente se muestra en la siguiente figura.
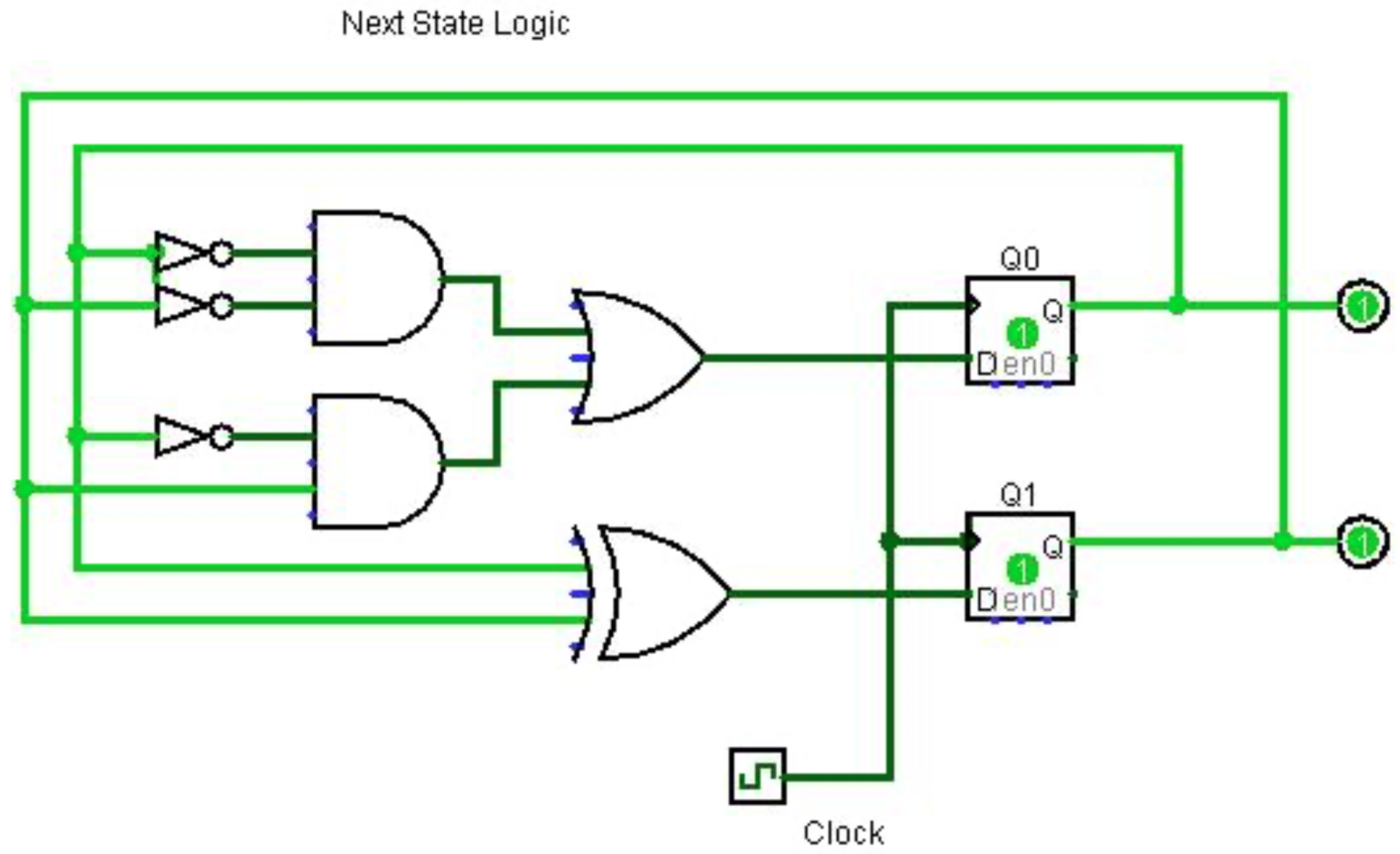
En esta figura, la siguiente lógica de estado se implementa usando puertas NOT, AND, OR y XOR. En realidad es un tipo de micro programa que se implementa en hardware. Esto se llama cableado porque el circuito real para calcular el siguiente estado está cableado en el circuito.
El problema con los programas cableados es que no se pueden cambiar fácilmente. Las computadoras modernas generalmente no implementan los microprogramas cableándolos, sino que utilizan algún tipo de memoria de solo lectura.
\(\PageIndex{4}\)Memoria de solo lectura
La memoria de solo lectura (ROM) es una memoria que nunca se escribe después de que se programa por primera vez 10. Se puede utilizar para almacenar programas que se utilizan para arrancar inicialmente una computadora, o para almacenar tablas de datos estáticos o microprogramas utilizados para especificar cómo funciona el hardware interno de la CPU. El siguiente es un ejemplo del contador Mod 4 que se muestra usando un chip ROM para implementar la siguiente lógica de estado como un micro programa.
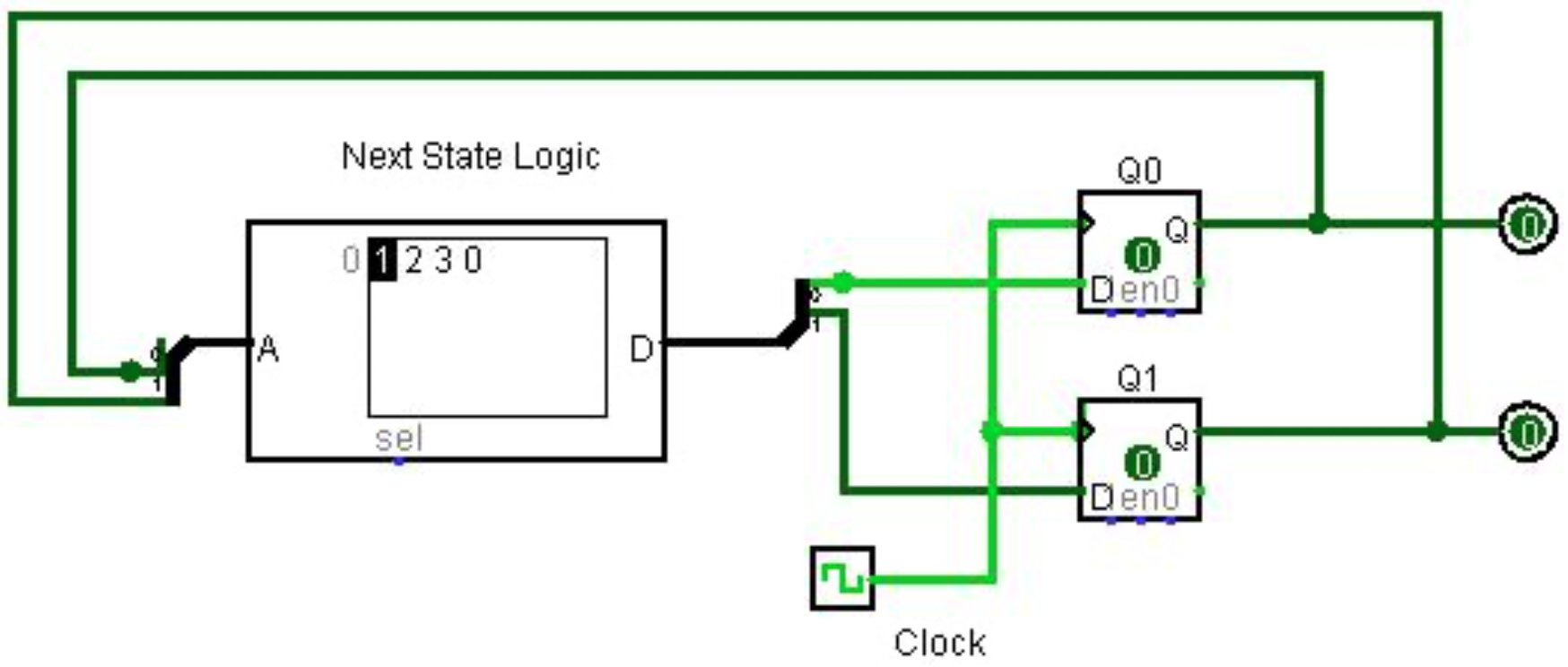
El chip ROM contiene el micro programa que implementa el Contador Mod 4. El siguiente estado para el contador mod 4 (1, 2, 3 y 0, o 00 2, 01 2, 10 2, 11 2) se almacena en una dirección correspondiente al estado actual del contador mod 4. Así, en la dirección 0 el programa ROM almacena 1, para afirmar que el siguiente estado de 0 es 1.
La dirección es el estado actual del contador, que es el valor actualmente almacenado en los registros. En la dirección 0, se almacena el valor 1, lo que dice que cuando Q 0 y Q 1 son 00 2, la ROM leerá el valor 01 2 de la memoria. Cada vez que el reloj marca, el chip ROM envía el siguiente valor a los registros, que pasa al siguiente estado en el contador.
Los chips ROM son una muy buena manera de implementar tablas de transición de estado, pero requieren hardware especial para crear y programar los chips ROM. Por lo que se utilizará un simple truco para implementar ROM para nuestros circuitos, como se hizo en el circuito switch mirroring en la sección 8-6. Este truco es usar un multiplexor con entrada cableada para el micro programa, y los bits de selección utilizados para especificar la dirección. Este diseño se muestra en la Figura\(\PageIndex{6}\).
Para entender este circuito, darse cuenta de que cada MUX elige 1 bit para cada uno de los 4 estados. Entonces cuando el estado es 00 2, el MUX inferior elegirá el bit 0 y el MUX superior seleccionará un bit 1, lo que da un nuevo estado de 01 2.
Este circuito que utiliza los dos MUXES para implementar el micro programa se mostrará en la siguiente sección.
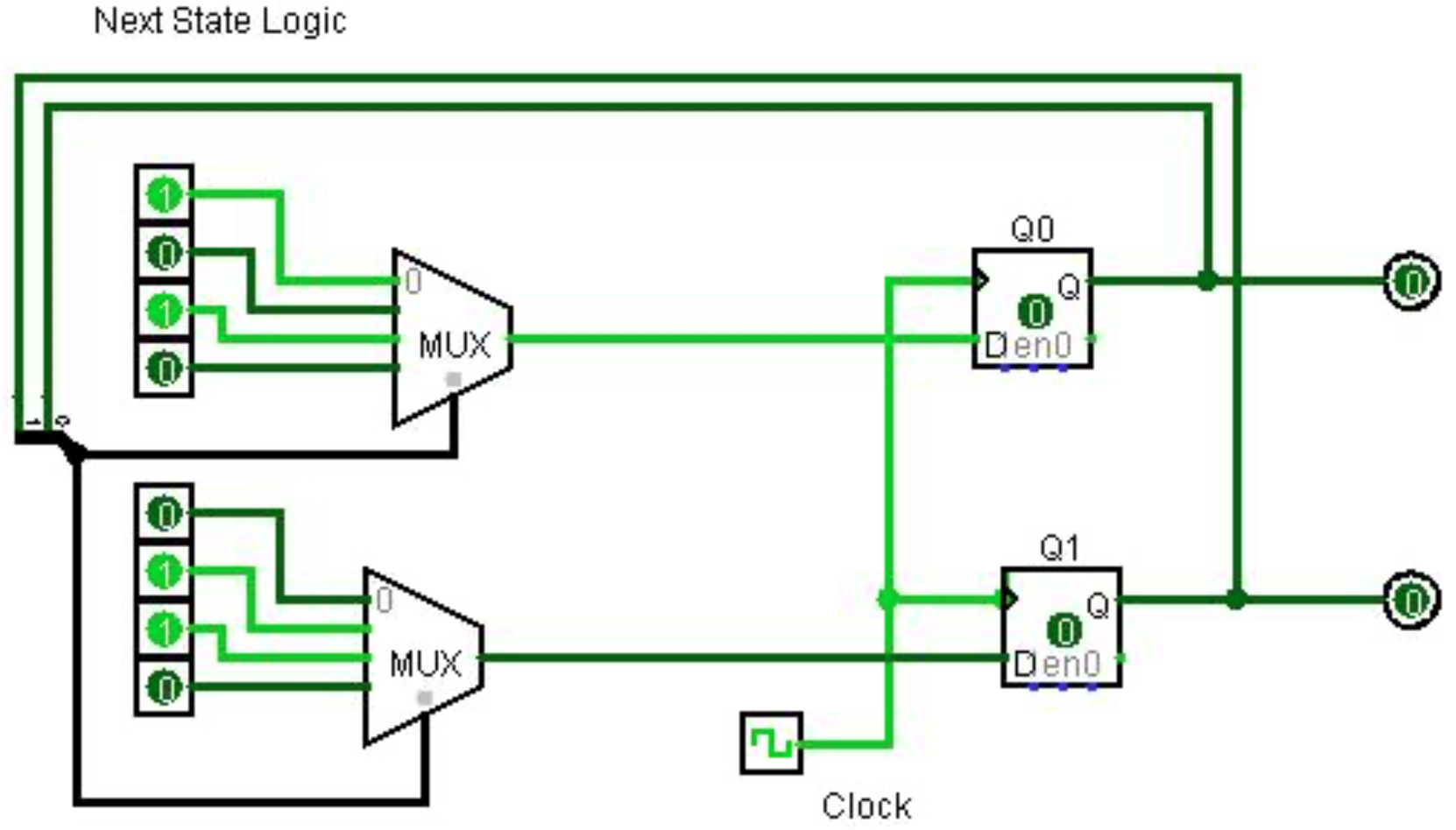
\(\PageIndex{5}\)Implementación del contador Mod 4
Figura\(\PageIndex{9}\) implementa el contador Mod 4. Los pasos 1 y 2 son necesarios para implementar el debouncing para el circuito, y se presentan sin explicación de cómo funcionan. Este circuito generalmente funciona bien si el botón se presiona bruscamente y limpiamente, pero a veces aún se generarán múltiples señales por el botón pulsador.
- Coloque el interruptor de botón pulsador en la placa. El interruptor sí tiene dirección, por lo que debe insertarse correctamente para que funcione. La forma más fácil de obtener la dirección correcta es colocar el interruptor a través del centro recortado en la placa de pruebas. Debido a que las patas del botón están enganchadas, solo hay una dirección para insertar el pulsador, y esa es la dirección correcta.
Conecte la entrada del chip al riel negativo. La salida del interruptor pulsador debe estar conectada a la entrada del inversor 7414 Schmitt en el paso 2. La salida del interruptor también debe estar conectada al riel negativo por un condensador de 0.1μf. Este condensador es absolutamente necesario para que el circuito funcione correctamente.
- Coloque el chip inversor 7414 Schmitt en la placa y enciéndalo. La salida del chip 7414 son las dos entradas de reloj para el chip 7474 en el paso 7.
- Coloque el chip multiplexor 74153 en la placa y enciéndalo. El diseño de pines para el multiplexor 74153 se muestra en la Figura\(\PageIndex{7}\). El paso 7 discutirá cómo cablear el chip para conectarlo al circuito. Los pasos a continuación discuten cómo cablearlo.
- Alimentar el chip con GND en el pin 8 y Vcc en el pin 16, como de costumbre.
- Los pines 1 y 15 se habilitan bajo. Estos permiten la salida de cada MUX. Siempre queremos la salida de los MUXES, así que habilitarlos conectando estos pines a baja.
Figura\(\PageIndex{7}\): Diagrama de diseño de 74153 pines 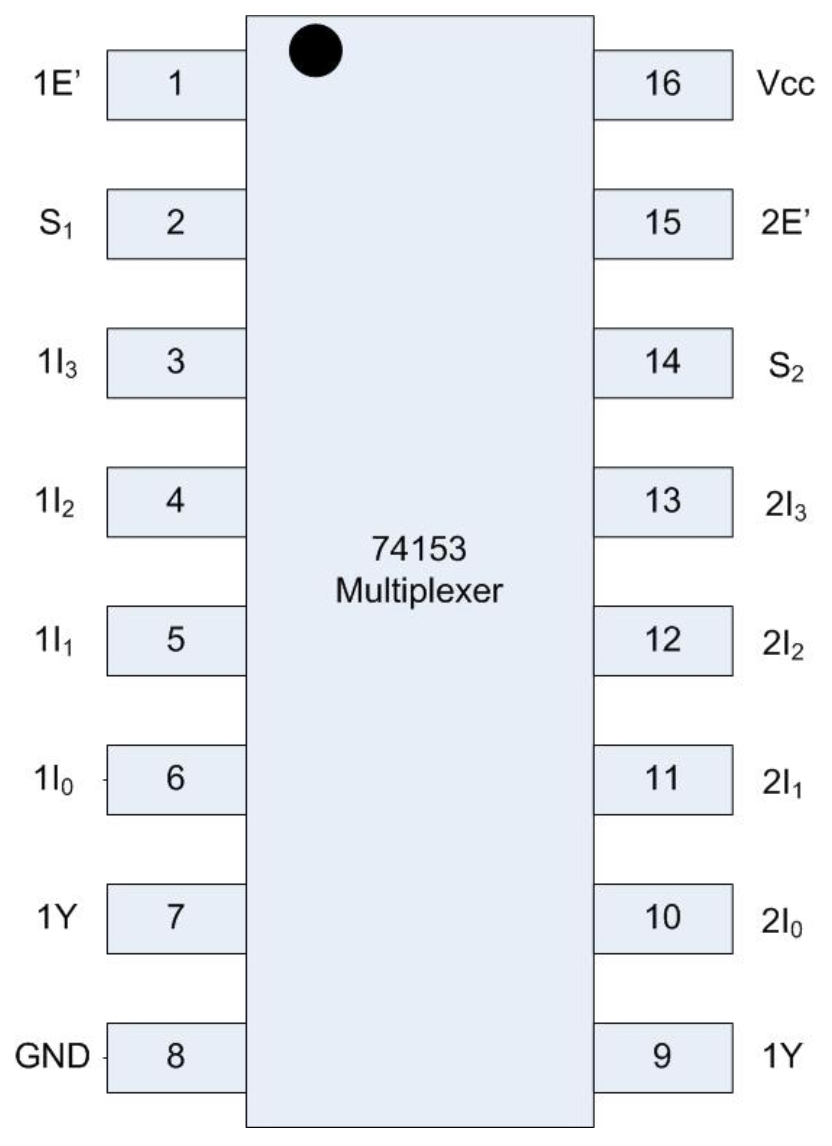
- Los pines 3... 7 y los pines 10... 14 son las entradas a cada MUX. Estos pines están establecidos para implementar el programa.
Nota
Los pasadores se establecen desde I 0... I 3 en dirección ascendente, no hacia abajo. Implementar el programa en la Figura\(\PageIndex{6}\) usando valores 1I de 0110 y valores 2I de 1010.
Figura\(\PageIndex{8}\): Diseño de pin 7474 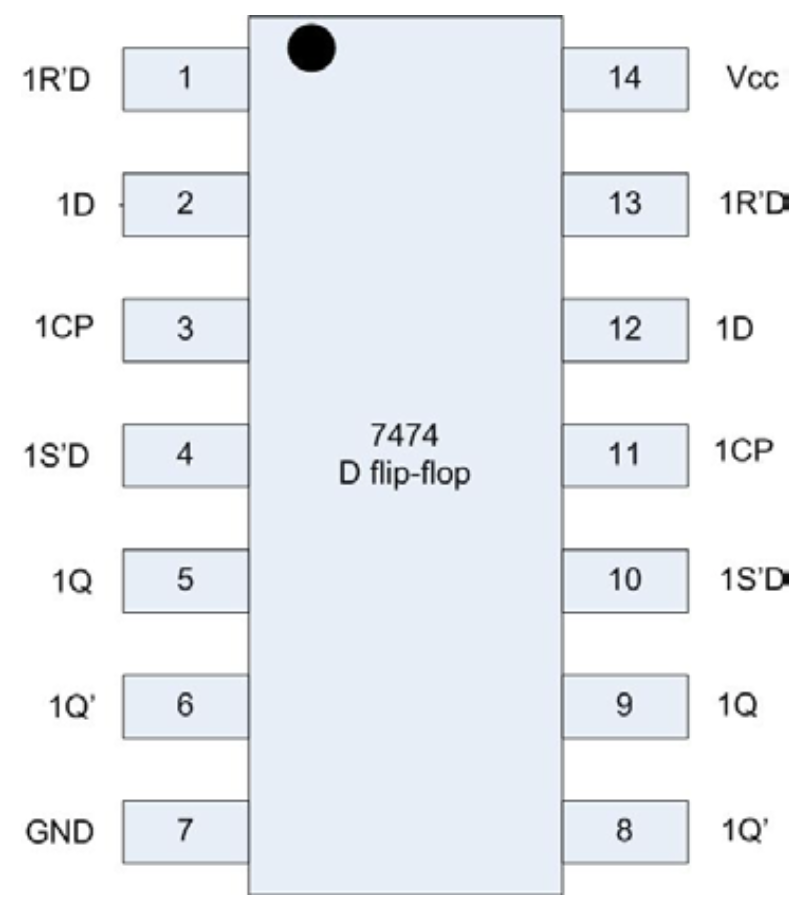
- Coloque el chip biestable D de 2 bits 7474 en la placa y enciéndalo. El diseño del pin del chip 7474 está en la Figura\(\PageIndex{8}\). El paso 8 discutirá cómo cablear el chip para conectarlo al circuito. Los pasos a continuación discuten cómo cablearlo.
- Alimentar el chip con GND en el pin 7 y Vcc en el pin 8, como de costumbre.
- Los pines 1, 4, 10 y 13 son para establecer y restablecer asíncronos. Están habilitados bajo, así que conecta estos pines al riel positivo para desactivarlos.
- Conecte el interruptor de botón a la entrada a una puerta (pin 1) en el inversor 7414 Schmitt. La salida de esta puerta (pin 2) se utilizará para ambos relojes en el chip biestables D 7474 de 2 bits.
- Conecte el chip 74153 (paso 3) al circuito. Las entradas S1 y S0 (pines 2 y 14) son las salidas del estado anterior, almacenadas en los biestables D en el paso 4. Estas entradas utilizan cables verdes para mostrar que se reciclan de la salida de un chip más abajo en el circuito. Las salidas del chip 74153 (pines 7 y 9) son la entrada D para el siguiente estado a los registros.
- Conecte las entradas D para el flip-flop D de 2 bits 7474 a los pines 2 y 12. Las entradas de reloj del paso 2 están conectadas a los pines 3 y 11. Las salidas son el estado actual en 1Q y 2Q, pines 6 y 9. Estas salidas se utilizan como entradas a la siguiente lógica de estado implementada en el MUX (paso 6, el cable verde), y para mostrar el estado actual representado en los LEDs de salida.
Figura\(\PageIndex{9}\): Contador Mod 4 
Cuando se presiona el interruptor de botón, las luces LED deben pasar por los estados para 00->01->10->11->00.
9 El contador de nombre mod 4 es más preciso porque el contador de 2 bits podría usarse para implementar un contador mod 3 o mod 4. Esto es más un problema con un contador de 4 bits porque a menudo se usa como contador de década (mod 10) o un contador hexadecimal (mod 16).
10 chips ROM y PROM nunca se cambian una vez que están escritos. Algunos tipos de chips similares a los chips ROM, como EPROM o EEPROM, se pueden escribir para almacenar un nuevo programa. Pero incluso estos tipos de chips ROM se escriben con poca frecuencia, y no están destinados a almacenar datos transitorios.


