2.4: Parámetros de dispersión generalizada

Los parámetros de dispersión hasta ahora se conocen como\(S\) parámetros normalizados porque tienen la misma impedancia de referencia en cada puerto. Sin embargo, no se utiliza la calificación 'normalizada' a menos que sea necesario distinguirlos de una forma más general de\(S\) parámetros. En esta sección se consideran\(S\) parámetros generalizados que tienen diferentes impedancias de referencia en cada uno de los puertos. Estos son particularmente útiles en el diseño de amplificadores pero también son útiles en mediciones donde la impedancia del sistema de un diseño puede no ser la misma que la impedancia de referencia del sistema de medición. Por ejemplo, un RFIC puede tener una impedancia del sistema de\(100\:\Omega\), pero el sistema de medición tiene una impedancia de referencia de\(50\:\Omega\).

2.4.1 La red\(N\) -Port

La red\(N\) -port es una generalización de una de dos puertos, como habrás adivinado. En la Figura 2.3.10 se muestra una red con muchos puertos. Nuevamente, cada puerto consta de un par de terminales, uno de los cuales es la referencia para voltaje. Cada puerto tiene corrientes iguales y opuestas en los dos terminales. Los voltajes incidente y reflejado en cualquier puerto pueden relacionarse entre sí usando la relación de matriz de parámetros de dispersión de voltaje:

\[\label{eq:1}\left[\begin{array}{c}{V_{1}^{-}}\\{V_{2}^{-}}\\{\vdots}\\{V_{N}^{-}}\end{array}\right]=\left[\begin{array}{cccc}{S_{11}}&{S_{12}}&{\cdots}&{S_{1N}} \\ {S_{21}}&{S_{22}}&{\cdots}&{S_{2N}} \\ {\vdots}&{}&{\ddots}&{}\\{S_{N1}}&{S_{N2}}&{\cdots}&{S_{NN}}\end{array}\right]=\left[\begin{array}{c}{V_{1}^{+}}\\{V_{2}^{+}}\\{\vdots}\\{V_{N}^{+}}\end{array}\right] \]

o en forma compacta como

\[\label{eq:2}\mathbf{V}^{-}=\mathbf{SV}^{+} \]

Observe que

\[\label{eq:3}S_{ij}=\left.\frac{V_{i}^{-}}{V_{j}^{+}}\right|_{V_{k}^{+}=0\text{ for }k\neq j} \]

En palabras,\(S_{ij}\) se encuentra al conducir Port\(j\) con una onda incidente de voltaje\(V_{j}^{+}\) y medir la onda reflejada\(V_{i}^{−}\) en Port\(i\), con todos los puertos que no sean\(j\) terminados en una carga emparejada. Los coeficientes de reflexión y transmisión también se pueden definir usando la relación anterior, siempre que los puertos se terminen en cargas coincidentes:

• \(S_{ii}\): coeficiente de reflexión visto mirando hacia el puerto\(i\)
• \(S_{ij}\): coeficiente de transmisión de\(j\) a\(i\).

2.4.2 Ondas de potencia

Los\(S\) parámetros utilizados hasta ahora tienen la misma impedancia de referencia en cada puerto. Estos pueden generalizarse para que las impedancias de referencia en cada puerto puedan ser diferentes. Estos son útiles si el sistema real que se está considerando tiene diferentes condiciones de carga en los puertos. \(S\)Los parámetros generalizados, denotados aquí como\(^{G}S\), se definen en términos de lo que se llama ondas de potencia raíz, que a su vez se definen usando ondas de voltaje de avance y retroceso. Considere la red\(N\) -port de la Figura 2.3.10, donde el puerto\(n\) th tiene una línea de transmisión de referencia de impedancia característica\(Z_{0n}\), que puede tener longitud infinitesimal. La línea de transmisión en el puerto\(n\) th sirve para separar las ondas de voltaje (y) y de corriente (\(V_{n}^{+}\)y\(V_{n}^{−}\)) que viajan hacia adelante\(I_{n}^{+}\) y\(I_{n}^{−}\) hacia atrás.

La matriz de impedancia característica de referencia\(\mathbf{Z}_{0}\) es una matriz diagonal\(\mathbf{Z}_{0} = \text{diag}(Z_{01}\ldots Z_{0n}\ldots Z_{0N})\),, y las ondas de potencia raíz en el puerto\(n\) th,\(a_{n}\) y\(b_{n}\), se definen por

\[\label{eq:4}a_{n}=V_{n}^{+}/\sqrt{\Re\{Z_{0n}\}}\quad\text{and}\quad b_{n}=V_{n}^{-}\sqrt{\Re\{Z_{0n}\}} \]

y se muestran en Figura\(\PageIndex{1}\) y a menudo se llaman solo ondas de energía. La unidad de los\(b\) valores\(a\) y es la potencia raíz, es decir, en el sistema de unidades SI,\(\sqrt{\text{W}}\). En forma de matriz

\[\begin{align}\label{eq:5}\mathbf{a}&=\mathbf{Z}_{0}^{-1/2}\mathbf{V}^{+}=\mathbf{Y}_{0}^{1/2}\mathbf{V}^{+} &\mathbf{b}&=\mathbf{Z}_{0}^{-1/2}\mathbf{V}^{-}=\mathbf{Y}_{0}^{1/2}\mathbf{V}^{-} \\ \label{eq:6}\mathbf{V}^{+}&=\mathbf{Z}_{0}^{1/2}\mathbf{a}=\mathbf{Y}_{0}^{-1/2}\mathbf{a} &\mathbf{V}^{-}&=\mathbf{Z}_{0}^{1/2}\mathbf{b}=\mathbf{Y}_{0}^{-1/2}\mathbf{b}\end{align} \]

donde

\[\begin{align}\label{eq:7}\mathbf{a}&=[a_{1}\ldots a_{n}\ldots a_{N}]^{\text{T}} &\mathbf{b}&=[b_{1}\ldots b_{n}\ldots b_{N}]^{\text{T}} \\ \label{eq:8}\mathbf{V}^{+}&=[V_{1}^{+}\ldots V_{n}^{+}\ldots V_{N}^{+}]^{\text{T}} &\mathbf{V}^{-}&=[V_{1}^{-}\ldots V_{n}^{-}\ldots V_{N}^{-}]^{\text{T}}\end{align} \]

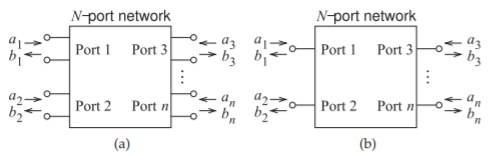
Figura\(\PageIndex{1}\):\(N\) -puertos que definen las ondas de potencia\(a\) y\(b\) raíz: (a) puertos de dos terminales; y (b) puertos por sí mismos.

y la matriz de admisión característica es\(\mathbf{Y}_{0} =\mathbf{Z}_{0}^{−1}\). Las ondas de potencia se interpretan como que describen el flujo de potencia:

\[\frac{1}{\sqrt{2}}|a_{n}|=\sqrt{\text{incident power at Port }n}\nonumber \]

y

\[\label{eq:9}\frac{1}{\sqrt{2}}|b_{n}|=\sqrt{\text{power leaving at Port }n} \]

Es decir, por ejemplo, la potencia incidente (o disponible) en Puerto\(n\), a la que se hace referencia\(Z_{0n}\), es\(\frac{1}{2}|a_{n}|^{2}\) y la potencia reflejada en el puerto es\(\frac{1}{2}|b_{n}|^{2}\). Así la potencia entregada por el puerto\(n\) th es\(\frac{1}{2}(|b_{n}|^{2} − |a_{n}|^{2})\).

Después de alguna manipulación se puede demostrar que en cada línea de referencia las ondas de potencia pueden relacionarse con los voltajes y corrientes totales como

\[\label{eq:10}\mathbf{a}=\frac{\mathbf{V}+\mathbf{Z}_{0}\mathbf{I}}{2\sqrt{\Re\{\mathbf{Z}_{0}\}}}\quad\text{and}\quad\mathbf{b}=\frac{\mathbf{V}-\mathbf{Z}_{0}^{\ast}\mathbf{I}}{2\sqrt{\Re\{\mathbf{Z}_{0}\}}} \]

donde\(\mathbf{V}\) y\(\mathbf{I}\) son vectores de voltaje total y corriente total. Ahora,\(S\) los parámetros generalizados pueden definirse formalmente como

\[\label{eq:11}\mathbf{b}=\:^{G}\mathbf{Sa} \]

así\(\mathbf{Y}_{0}^{1/2}\mathbf{V}^{−} =\:^{G}\mathbf{SY}_{0}^{1/2}\mathbf{V}^{+}\), y así\(\mathbf{V}^{−} = \mathbf{Y}_{0}^{−1/2}\:^{G}\mathbf{SY}_{0}^{1/2}\mathbf{V}^{+}\). Esto se reduce a\(\mathbf{V}^{−} =\:^{G}\mathbf{SV}^{+}\) cuando todas las líneas de transmisión de referencia tienen la misma impedancia característica. Sin embargo, cuando los puertos tienen diferentes impedancias de referencia,\(\mathbf{S}^{V}\) se utiliza para parámetros de dispersión de voltaje y\(\mathbf{S}^{I}\) para parámetros de dispersión de corriente, dónde\(\mathbf{V}^{−}= \mathbf{S}^{V}\mathbf{V}^{+}\) y\(\mathbf{I}^{−}= \mathbf{S}^{I}\mathbf{I}^{+}\).

También se pueden derivar las siguientes relaciones de conversión:

\[\begin{align}\label{eq:12}\mathbf{S}^{I}&=\Re\{\mathbf{Z}_{0}\}^{-\frac{1}{2}G}\mathbf{S}\Re\{\mathbf{Z}_{0}\}^{\frac{1}{2}} \\ \label{eq:13} \mathbf{S}^{V}&=\mathbf{Z}_{0}\Re\{\mathbf{Z}_{0}\}^{-\frac{1}{2}G}\mathbf{S}\Re\{\mathbf{Z}_{0}\}^{\frac{1}{2}}\{\mathbf{Z}_{0}^{\ast}\}^{-1}\end{align} \]

donde\(\Re\{\mathbf{Z}_{0}\}^{\frac{1}{2}}=\text{diag}\{\sqrt{\Re\{Z_{01}\}},\:\sqrt{\Re\{Z_{02}\}},\ldots\sqrt{\Re\{Z_{0n}\}}\}\).

Recordemos que\(^{G}\mathbf{S}\) es en términos de\(\mathbf{a}\) y\(\mathbf{b}\),\(\mathbf{S}^{\mathbf{I}}\) es en términos de\(\mathbf{I}^{−}\) y\(\mathbf{I}^{+}\), y\(\mathbf{S}^{\mathbf{V}}\) es en términos de\(\mathbf{V}^{−}\) y\(\mathbf{V}^{+}\). Cuando las impedancias de puerto y las resistencias de referencia son reales, Ecuaciones\(\eqref{eq:12}\) y\(\eqref{eq:13}\) asumir las formas más simples

\[\begin{align}\label{eq:14}\mathbf{S}^{I}&=-\mathbf{R}_{0}^{-\frac{1}{2}}\:^{G}\mathbf{S}\mathbf{R}_{0}^{\frac{1}{2}}=-\:^{G}\mathbf{S} \\ \label{eq:15}\mathbf{S}^{\mathbf{V}}&=\mathbf{R}_{0}\mathbf{R}_{0}^{-\frac{1}{2}}\:^{G}\mathbf{S}\mathbf{R}_{0}^{\frac{1}{2}}\mathbf{R}_{0}^{\ast^{-1}}=\mathbf{R}_{0}(\mathbf{R}_{0}^{\ast})^{-1}\:^{G}\mathbf{S}=^{G}\mathbf{S}\end{align} \]

donde\(\mathbf{R}_{0}^{\frac{1}{2}}=\text{diag}\{\sqrt{R_{01}},\:\sqrt{R_{02}},\ldots ,\sqrt{R_{0n}}\}\),\(R_{0n}\) siendo la resistencia de referencia en el puerto n. Además, si las resistencias de referencia en cada puerto son las mismas, todas las diversas definiciones de parámetros de dispersión se vuelven equivalentes (es decir,\(\mathbf{S}^{\mathbf{V}} = −\mathbf{S}^{\mathbf{I}} =\:^{G}\mathbf{S} = \mathbf{S}\)), donde\(\mathbf{S}\) está la matriz de\(S\) parámetros normalizada, también llamada matriz de\(S\) parámetros normalizada.

La condición de reciprocidad para los\(S\) parámetros generalizados es\(^{G}S_{12} =\:^{G}S_{21}Z_{01}/Z_{02}\).

Ejemplo\(\PageIndex{1}\): Generalized Scattering Parameters of a Through Connection

Desarrollar los parámetros de dispersión generalizados de una conexión pasante con una impedancia de referencia\(Z_{01}\) en Port\(\mathsf{1}\) y una impedancia de referencia\(Z_{02}\) en Port\(\mathsf{2}\).

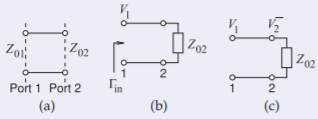
Figura\(\PageIndex{2}\)

Solución

La conexión pasante se muestra en (a) y en (b) es la configuración a determinar\(S_{11}\) como\(V_{2}^{+}=0= a_{2}\) ya que Port\(\mathsf{2}\) se termina en\(Z_{02}\). Entonces

\[\label{eq:16}^{G}S_{11}=\Gamma_{\text{in}}=\frac{Z_{02}-Z_{01}}{Z_{02}+Z_{01}}\quad\text{and similarly}\quad ^{G}S_{22}=\frac{Z_{01}-Z_{02}}{Z_{02}+Z_{01}}=-\:^{G}S_{11} \]

La Figura (b) se utiliza para determinar\(S_{21}\) como aquí\(V_{2}^{+}=0= a_{2}\)

\[\label{eq:17}V_{2}^{-}=b_{2}\sqrt{\Re\{Z_{02}\}}=V_{1}=V_{1}^{+}+V_{1}^{-}=V_{1}^{+}(1+S_{11})=a_{1}\sqrt{\Re\{Z_{01}\}} \]

Por lo tanto,

\[\label{eq:18}^{G}S_{21}=\left.\frac{b_{2}}{a_{1}}\right|_{a_{2}=0}=\frac{\sqrt{\Re\{Z_{01}\}}}{\sqrt{\Re\{Z_{02}\}}}(1+\:^{G}S_{11})\quad\text{and also}\quad ^{G}S_{12}=\frac{\sqrt{\Re\{Z_{02}\}}}{\sqrt{\Re\{Z_{01}\}}}(1+\:^{G}S_{22}) \]

La matriz de parámetros de dispersión generalizada del through es

\[\label{eq:19}^{G}\mathbf{S}=\frac{1}{Z_{01}+Z_{02}}\left[\begin{array}{cc}{Z_{02}-Z_{01}}&{2Z_{01}\sqrt{\Re\{Z_{02}\}/\Re\{Z_{01}\}}}\\{2Z_{02}\sqrt{\Re\{_{01}\}/\Re\{Z_{02}\}}}&{Z_{01}-Z_{02}}\end{array}\right] \]

y de verdad\(Z_{01}\) y\(Z_{02}\)

\[\label{eq:20}^{G}\mathbf{S}=\frac{1}{Z_{01}+Z_{02}}\left[\begin{array}{cc}{Z_{02}-Z_{01}}&{2\sqrt{Z_{01}Z_{02}}}\\{2\sqrt{Z_{01}Z_{02}}}&{Z_{01}-Z_{02}}\end{array}\right] \]

Para\(S\) los parámetros normalizados las impedancias de referencia en los puertos son las mismas, es decir\(Z_{01} = Z_{0} = Z_{02}\), y los\(S\) parámetros normalizados del through son (como se esperaba)

\[\label{eq:21}\mathbf{S}=\:^{N}\mathbf{S}=\left[\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}\right] \]

2.4.3 Parámetros de dispersión en términos de\(a\) y\(b\) ondas

Anteriormente\(S\) los parámetros se definieron en términos de ondas de voltaje de avance y retroceso, ver Sección 2.3.3 y Ecuación (2.3.15). Esa definición es adecuada si solo se usa una impedancia de referencia en todas partes. Una forma más general de\(S\) parámetros utiliza las ondas de potencia\(a\) y\(b\) raíz. Esto sigue siendo válido si solo se usa una impedancia de referencia pero también se pueden usar cuando los puertos tienen diferentes impedancias de referencia. Esta definición más general para una red de dos puertos, con respecto a la Figura\(\PageIndex{3}\), es

\[\label{eq:22}\left[\begin{array}{c}{b_{1}}\\{b_{2}}\end{array}\right]=\left[\begin{array}{cc}{S_{11}}&{S_{12}}\\{S_{21}}&{S_{22}}\end{array}\right]\left[\begin{array}{c}{a_{1}}\\{a_{2}}\end{array}\right] \]

Incluso si las impedancias de referencia en los puertos\(\mathsf{1}\) y\(\mathsf{2}\) son las diferentes. Si la impedancia de referencia es la misma y real, el caso habitual, los parámetros de dispersión son idénticos cuando se utilizan para relacionar ondas de voltaje de desplazamiento como en los siguientes:

\[\label{eq:23}\left[\begin{array}{c}{V_{1}^{-}}\\{V_{2}^{-}}\end{array}\right]=\left[\begin{array}{cc}{S_{11}}&{S_{12}}\\{S_{21}}&{S_{22}}\end{array}\right]\left[\begin{array}{c}{V_{1}^{+}}\\{V_{2}^{+}}\end{array}\right] \]

2.4.4\(S\) Parámetros normalizados y generalizados

\(S\)los parámetros medidos con respecto a una resistencia de referencia común se denominan\(S\) parámetros normalizados. En casi todos los casos, los\(S\) parámetros medidos se normalizan a\(50\:\Omega\), ya que\(50\:\Omega\) los cables y componentes se utilizan en los sistemas de medición. En otras palabras,\(Z_{01} = Z_{02} =\ldots= Z_{0N} = R_{0} (= 50\:\Omega)\). \(S\)Los parámetros generalizados se pueden utilizar para simplificar el proceso de diseño de dispositivos como amplificadores. Por ejemplo, a menudo es conveniente usar las impedancias de entrada y salida de un amplificador como impedancias de normalización. Además, a menudo es deseable poder convertir entre\(S\) parámetros medidos (normalizados a\(50\:\Omega\)) y\(S\) parámetros generalizados. Dejar\(^{N}\mathbf{S}\) ser la matriz de\(S\) parámetros medida (normalizada). (Así\(^{N}\mathbf{S}\) es la matriz de\(S\) parámetros convencional.) El desarrollo es tedioso, pero se puede demostrar que los\(S\) parámetros generalizados son

\[\label{eq:24}^{G}\mathbf{S}=(\mathbf{D}^{\ast})^{-1}(\:^{N}\mathbf{S}-\mathbf{Γ}^{\ast})(\mathbf{U}-\mathbf{Γ}\:^{N}\mathbf{S})^{-1}\mathbf{D} \]

donde\(\mathbf{U}\) está la matriz unitaria\((\mathbf{U} = \text{diag}(1, 1,..., 1))\),\(R_{0}\) es la impedancia de referencia de los\(S\) parámetros normalizados\(^{N}\mathbf{S}\), y\(\mathbf{D}\) es una matriz diagonal con elementos

\[\begin{align}\label{eq:25}D_{ii}&=|1-\Gamma_{i}^{\ast}|^{-1}(1-\Gamma_{i})\sqrt{1-|\Gamma_{i}|^{2}} \\ \label{eq:26}\Gamma_{i}&=(Z_{0i}-R_{0})(Z_{0i}+R_{0})^{-1}\quad i=1,2,\ldots ,N\end{align} \]

y\(\mathbf{Γ}\) es una matriz diagonal con elementos\(\Gamma_{i}\). \(Z_{0i}\)es la impedancia del sistema en el puerto\(i\) al que se van a referir los\(S\) parámetros generalizados.

2.4.5 Cambio de Impedancia de Referencia

El resultado en la sección anterior se puede usar para cambiar los parámetros de dispersión referenciados a una impedancia real\(R_{1}\) (es decir,\(^{R1}\mathbf{S}\)) a parámetros de dispersión referenciados a\(R_{2}\) (es decir,\(^{R2}\mathbf{S}\)). Tenga en cuenta que\(^{R1}\mathbf{S}\) y\(^{R2}\mathbf{S}\) son los\(S\) parámetros convencionales o normalizados. Los elementos en Ecuaciones\(\eqref{eq:25}\) y\(\eqref{eq:26}\) se convierten

\[\begin{align}\label{eq:27}D_{ii}&=D=|1-\Gamma_{R2}|^{-1}(1-\Gamma_{R2})\sqrt{1-|\Gamma_{R2}|^{2}}=\sqrt{1-|\Gamma_{R2}|^{2}} \\ \label{eq:28}\Gamma_{R2}&=(R_{2}-R_{1})(R_{2}+R_{1})^{-1}\end{align} \]

y\(|\Gamma_{R2}| < 1\). Así que la ecuación\(\eqref{eq:24}\) se convierte

\[\label{eq:29}^{R2}\mathbf{S}=\mathbf{D}^{-1}(\:^{R1}\mathbf{S}-\mathbf{Γ})(\mathbf{U}-\mathbf{Γ}^{R1}\:\mathbf{S})^{-1}\mathbf{D}=(\:^{R1}\mathbf{S}-\mathbf{Γ})(\mathbf{U}-\mathbf{Γ}^{R1}\:\mathbf{S})^{-1} \]

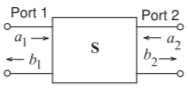
Figura\(\PageIndex{3}\): Definición de\(S\) parámetros en términos de ondas\(a\) de potencia\(b\) radiculares. \(a_{1} = V_{1}^{+}/\Re\{Z_{01}\},\: b_{1} = V_{1}^{−}/\Re\{Z_{01}\},\: a_{2} = V_{2}^{+}/\Re\{Z_{02}\},\: b_{2} = V_{2}^{−}/\Re\{Z_{02}\}\). El poder incidente en el Puerto\(\mathsf{1}\) (2) es\(|a_{1}|^{2} (|a_{2}^{2})\). El poder que sale del puerto\(\mathsf{1}\) (2) es\(|b_{1}|^{2} (|b_{2}^{2})\)

ya que\(\mathbf{D}\) es una matriz diagonal con todas las entradas diagonales iguales. Así que para un puerto de dos

\[\begin{align} ^{R2}\mathbf{S}&=\left[\begin{array}{cc}{^{R2}S_{11}}&{^{R2}S_{12}} \\ {^{R2}S_{21}}&{^{R2}S_{22}}\end{array}\right] \nonumber \\ \label{eq:30}&=\left[\begin{array}{cc}{^{R1}S_{11}-\Gamma_{R2}}&{^{R1}S_{12}} \\ {^{R1}S_{21}}&{^{R1}S_{22}-\Gamma_{R2}}\end{array}\right] \left[\begin{array}{cc}{1-\Gamma_{R2}\:^{R1}S_{11}}&{-\Gamma_{R2}\:^{R1}S_{12}} \\ {-\Gamma_{R2}\:^{R1}S_{21}}&{1-\Gamma_{R2}\:^{R1}S_{22}}\end{array}\right] ^{-1} \end{align} \]

Ejemplo\(\PageIndex{2}\): Change of Reference Impedance

Un atenuador tiene los\(50\:\Omega\: S\) parámetros:

\[\label{eq:31}^{50}\mathbf{S}=\left[\begin{array}{cc}{0}&{0.3162} \\ {0.3162}&{0}\end{array}\right] \]

¿A qué se hace referencia a los\(S\) parámetros\(75\:\Omega\)?

Solución

La conversión utiliza Ecuación\(\eqref{eq:30}\) con\(R_{1} = 50\:\Omega\) y\(R_{2} = 75\:\Omega\). Entonces\(\Gamma_{75} = (75 − 50)/(75 + 50) = 0.2\). Así los\(S\) parámetros a los que se hace referencia\(75\:\Omega\) son

\[\begin{align} ^{75}\mathbf{S}&=\left[\begin{array}{cc}{^{50}S_{11}-\Gamma_{75}}&{^{50}S_{12}} \\ {^{50}S_{21}}&{^{50}S_{22}-\Gamma_{75}}\end{array}\right] \left[\begin{array}{cc}{1-\Gamma_{75}\:^{50}S_{11}}&{-\Gamma_{75}\:^{50}S_{12}} \\ {-\Gamma_{75}\:^{50}S_{21}}&{1-\Gamma_{75}\:^{50}S_{22}}\end{array}\right] \nonumber \\ &=\left[\begin{array}{cc}{-0.2}&{0.3162} \\ {0.3162}&{-0.2}\end{array}\right] \left[\begin{array}{cc}{1}&{-0.2\cdot 0.3162} \\ {-0.2\cdot 0.3162}&{1}\end{array}\right]\nonumber \\ \label{eq:32}&=\left[\begin{array}{cc}{-0.2}&{0.3162} \\ {0.3162}&{-0.2}\end{array}\right] \left[\begin{array}{cc}{1}&{0.06324} \\ {0.06324}&{1}\end{array}\right] =\left[\begin{array}{cc}{-0.18}&{0.3036} \\ {0.3036}&{-0.18}\end{array}\right] \end{align} \]

2.4.6 Pasividad en términos de parámetros de dispersión

Consideremos un\(N\) puerto caracterizado por su matriz de dispersión generalizada\(\mathbf{S}\). La potencia promediada en el tiempo disipada en el\(N\) puerto es

\[\label{eq:33}P=\frac{1}{2}\sum_{i=1}^{N}(|a_{i}|^{2}-|b_{i}|^{2})=\frac{1}{2}(\mathbf{a}^{\ast^{\text{T}}}\mathbf{a}=\mathbf{b}^{\ast^{\text{T}}}\mathbf{b}) \]

y así

\[\label{eq:34}P=\frac{1}{2}\mathbf{a}^{\ast^{\text{T}}}[\mathbf{U}-(\mathbf{S}^{\ast})^{\text{T}}\mathbf{S}]\:\mathbf{a} \]

En lo anterior, el conjugado,\(\mathbf{a}^{\ast}\), de la matriz\(\mathbf{a}\) se obtiene de\(\mathbf{a}\) tomando el conjugado complejo de cada elemento. Para un\(N\) puerto pasivo,

\[\label{eq:35}\mathbf{U}-(\mathbf{S}^{\ast})^{\text{T}}\mathbf{S}\geq 0\quad\text{for all real }\omega \]

Esto también se puede escribir en forma de suma como

\[\label{eq:36}\sum_{k=1}^{N}S_{kj}S_{kj}^{\ast}=P_{j} \]

\(P_{j} = 1\)para todos\(j\) si la red es sin pérdidas. Para que una red sea pasiva\(P_{j} ≤ 1\) para todos\(j\). Al examinar los\(S\) parámetros se puede determinar rápidamente si una red es sin pérdidas, con pérdida o tal vez tiene ganancia.

Para un\(N\) puerto sin pérdidas,

\[\label{eq:37}\mathbf{U}-\mathbf{S}^{\ast^{\text{T}}}\mathbf{S}=0 \]

Reordenando, tomando la transposición de ambos lados y señalando que\(\mathbf{U}^{\text{T}} = \mathbf{U}\)

\[\label{eq:38}\mathbf{S}^{\ast}\mathbf{S}^{\text{T}}=\mathbf{U} \]

A esto se le conoce como la condición unitaria. Es decir, para un\(N\) puerto sin pérdidas

\[\label{eq:39}\mathbf{S}^{\ast}=(\mathbf{S}^{\text{T}})^{-1} \]

El resultado importante aquí es que para una red sin pérdidas (estas son las condiciones unitarias)

\[\begin{align}\label{eq:40}\sum_{k=1}^{N}S_{kj}S_{kj}^{\ast}&=1 \\ \label{eq:41}\sum_{k=1}^{N}S_{ki}S_{kj}^{\ast}&=0\quad\text{for }i\text{ not equal to }j\end{align} \]

2.4.7 Representación de la matriz de impedancia

En esta sección\(S\) los parámetros\(N\) -port están relacionados con los\(z\) parámetros\(N\) -port. La relación básica de voltaje y corriente en cualquier puerto usando impedancias es

\[\label{eq:42}\left[\begin{array}{c}{V_{1}}\\{V_{2}}\\{\vdots}\\{V_{N}}\end{array}\right]=\left[\begin{array}{cccc}{z_{11}}&{z_{12}}&{\cdots}&{z_{1N}} \\ {z_{21}}&{z_{22}}&{\cdots}&{z_{2N}} \\ {\vdots}&{}&{\ddots}&{} \\ {z_{N1}}&{z_{N2}}&{\cdots}&{z_{NN}}\end{array}\right]\left[\begin{array}{c}{I_{1}}\\{I_{2}}\\{\vdots}\\{I_{N}}\end{array}\right] \]

o en forma compacta como

\[\label{eq:43}\mathbf{V}=\mathbf{ZI} \]

\(\mathbf{Z}\)es recíproco si\(z_{ij} = z_{ji}\). Los\(z\) parámetros definidos aquí se denominan más formalmente parámetros z basados en puertos, ya que las variables de voltaje y corriente son cantidades de puerto.

La relación\(z\) y\(S\) los parámetros comienzan relacionando el voltaje total y la corriente en el plano terminal n con el voltaje de desplazamiento y las ondas de corriente. De la Figura 2.3.10,

\[\label{eq:44}V_{n}=V_{n}^{+}+V_{n}^{-}\quad\text{and}\quad I_{n}=I_{n}^{+}-I_{n}^{-} \]

y en forma de vector

\[\label{eq:45}\begin{align} \mathbf{V}&=\mathbf{V}^{+}+\mathbf{V}^{-} &\mathbf{I}&=\mathbf{I}^{+}+\mathbf{I}^{-} \\ \mathbf{V}^{+}&=\mathbf{Z}_{0}^{\ast}\mathbf{I}^{+} &\mathbf{V}^{-}&=-\mathbf{Z}_{0}\mathbf{I}^{-}\nonumber \end{align} \nonumber \]

donde\(\mathbf{Z}_{0} = \text{diag}(Z_{01},\: Z_{02},\ldots ,Z_{0N})\) (y\(z_{0n}\) puede ser complejo). Después de alguna manipulación algebraica, se obtienen las siguientes relaciones:

\[\begin{align}\label{eq:46}\mathbf{S}^{V}&=[\mathbf{U}+\mathbf{ZZ}_{0}^{-1}]^{-1}[\mathbf{Z}(\mathbf{Z}_{0}^{\ast})^{-1}-\mathbf{U}] \\ \label{eq:47}\mathbf{Z}&=[\mathbf{U}+\mathbf{S}^{V}][\mathbf{Z}_{0}^{\ast^{-1}}-\mathbf{Z}_{0}^{-1}(\mathbf{S}^{V})]^{-1}\end{align} \]

Tenga en cuenta que\(\mathbf{S}^{V}\) es la matriz de parámetros de dispersión de voltaje. Estos están relacionados con la matriz de parámetros de dispersión generalizada por Ecuación\(\eqref{eq:15}\). Para\(S\) parámetros normalizados se usa la misma impedancia de referencia real en todos los puertos\((Z_{0n} = Z_{0},\: n = 1,\ldots ,N)\), luego Ecuaciones\(\eqref{eq:46}\) y\(\eqref{eq:47}\) convertirse

\[\label{eq:48}\mathbf{S}=[\mathbf{Z}+Z_{0}\mathbf{U}]^{-1}[\mathbf{Z}-Z_{0}\mathbf{U}]\quad\text{and}\quad\mathbf{Z}=Z_{0}[\mathbf{U}+\mathbf{S}][\mathbf{U}-\mathbf{S}]^{-1} \]

2.4.8 Representación de Matriz de Admisión

En esta sección,\(S\) los parámetros\(N\) -port están relacionados con los\(y\) parámetros\(N\) -port. Las corrientes y voltajes se relacionan como

\[\label{eq:49}\left[\begin{array}{c}{I_{1}}\\{I_{2}}\\{\vdots}\\{I_{N}}\end{array}\right]=\left[\begin{array}{cccc}{y_{11}}&{y_{12}}&{\cdots}&{y_{1N}} \\ {y_{21}}&{y_{22}}&{\cdots}&{y_{2N}} \\ {\vdots}&{}&{\ddots}&{} \\ {y_{N1}}&{y_{N2}}&{\cdots}&{y_{NN}}\end{array}\right]\left[\begin{array}{c}{V_{1}}\\{V_{2}}\\{\vdots}\\{V_{N}}\end{array}\right] \]

o en forma compacta, los\(y\) parámetros basados en puertos son

\[\label{eq:50}\mathbf{I}=\mathbf{YV} \]

Utilizando un enfoque similar al de la subsección anterior, se puede desarrollar la relación entre\(S\) y\(y\) parámetros. El desarrollo se realizará de manera ligeramente diferente y este desarrollo es aplicable a parámetros de dispersión generalizados. Primero, considere la relación entre el voltaje\(\mathbf{V} = [V_{1}\ldots V_{n}\ldots V_{N}]^{\text{T}}\) y la corriente totales del puerto\(\mathbf{I} = [I_{1}\ldots I_{n}\ldots I_{N}]^{\text{T}}\) con el voltaje y las ondas de corriente que viajan hacia adelante y hacia atrás:

\[\label{eq:51}\mathbf{V}=\mathbf{V}^{+}+\mathbf{V}^{-}\quad\text{and}\quad\mathbf{I}=\mathbf{I}^{+}+\mathbf{I}^{-} \]

dónde\(\mathbf{I}^{+} = \mathbf{Y}_{0}\mathbf{V}^{+} = \mathbf{Y}_{0}^{1/2}\:\mathbf{a}\) y\(\mathbf{I}^{−} = −\mathbf{Y}_{0}\mathbf{V}^{−} = −\mathbf{Y}_{0}^{1/2}\:\mathbf{b}\). (Cada elemento de\(\mathbf{Y}_{0}\),\(Y_{0n} = 1/Z_{0n}\) y puede ser complejo.) Usando ondas viajeras, la ecuación\(\eqref{eq:50}\) se convierte

\[\begin{align}\label{eq:52}\mathbf{I}^{+}+\mathbf{I}^{-}&=\mathbf{Y}(\mathbf{V}^{+}+\mathbf{V}^{-}) \\ \label{eq:53}\mathbf{Y}_{0}(\mathbf{V}^{+}-\mathbf{V}^{-})&=\mathbf{Y}(\mathbf{V}^{+}+\mathbf{V}^{-}) \\ \label{eq:54}\mathbf{Y}_{0}(1-\mathbf{Y}_{0}^{-1/2}\mathbf{SY}_{0}^{1/2})\mathbf{V}^{+}&=\mathbf{Y}(1+\mathbf{Y}_{0}^{-1/2}\mathbf{SY}_{0}^{1/2})\mathbf{V}^{+}\end{align} \]

y así los\(y\) parámetros de puerto en términos de los parámetros de dispersión generalizada son

\[\label{eq:55}\mathbf{Y}=\mathbf{Y}_{0}(1-\mathbf{Y}_{0}^{-1/2}\:^{G}\mathbf{SY}_{0}^{1/2})(1+\mathbf{Y}_{0}^{-1/2}\:^{G}\mathbf{SY}_{0}^{1/2})^{-1} \]

Alternativamente, la ecuación se\(\eqref{eq:53}\) puede reorganizar como

\[\begin{align}\label{eq:56}(\mathbf{Y}_{0}+\mathbf{Y})\mathbf{V}^{-}&=(\mathbf{Y}_{0}-\mathbf{Y})\mathbf{V}^{+} \\ \label{eq:57}\mathbf{V}^{-}&=(\mathbf{Y}_{0}+\mathbf{Y})^{-1}(\mathbf{Y}_{0}-\mathbf{Y})\mathbf{V}^{+} \\ \label{eq:58}\mathbf{Y}_{0}^{-1/2}\mathbf{b}&=(\mathbf{Y}_{0}+\mathbf{Y})^{-1}(\mathbf{Y}_{0}-\mathbf{Y})\mathbf{Y}_{0}^{-1/2}\mathbf{a}\end{align} \]

Comparando esto con la definición de\(S\) parámetros generalizados en Ecuación\(\eqref{eq:11}\) lleva a

\[\label{eq:59}^{G}\mathbf{S}=\mathbf{Y}_{0}^{1/2}(\mathbf{Y}_{0}+\mathbf{Y})^{-1}(\mathbf{Y}_{0}-\mathbf{Y})\mathbf{Y}_{0}^{-1/2} \]

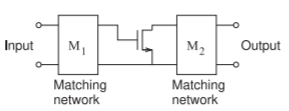
Figura\(\PageIndex{4}\): Un amplificador con un dispositivo activo y redes\((\text{M}_{2})\) coincidentes de entrada\((\text{M}_{1})\) y salida. No se muestra la disposición de polarización, pero generalmente esto se hace con la elección apropiada de topología de red coincidente.

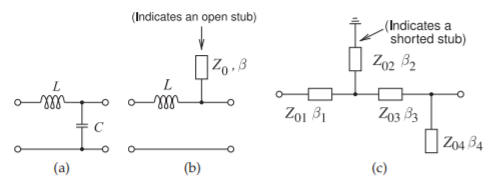
Figura\(\PageIndex{5}\): Tres formas de redes coincidentes con creciente uso de secciones de líneas de transmisión.

Para el caso habitual donde todas las líneas de transmisión de referencia tienen la misma impedancia característica\(Z_{0} = 1/Y_{0}\) (nota\(S =\:^{N}\mathbf{S}\)),

\[\label{eq:60}\mathbf{Y}=Y_{0}(\mathbf{U}-\mathbf{S})(\mathbf{U}+\mathbf{S})^{-1}\quad\text{and}\quad\mathbf{S}=(\mathbf{Y}_{0}+\mathbf{Y})^{-1}(\mathbf{Y}_{0}-\mathbf{Y}) \]