5.16: Ejercicios

1. La impedancia de salida equivalente Thevenin de cada uno de los amplificadores de la Figura 5.12.8 (a) es$5\:\Omega$, y la impedancia del sistema$R_{0}$, es$75\:\Omega$. Elija los devanados del transformador para la máxima transferencia de potencia. [Ejemplo de Parallels 5.12.4]
2. Un inductor espiral se modela como un inductor ideal de$10\text{ nH}$ en serie con una$5\:\Omega$ resistencia. ¿En qué$Q$ se encuentra el inductor espiral$1\text{ GHz}$?
3. Considera el diseño de un$\mathsf{T}$ atenuador$50\text{ dB}$ resistivo en un$75\:\Omega$ sistema. [Ejemplo de Parallels 5.5.1]
   1. Dibujar la topología del atenuador.
   2. Anote las ecuaciones de diseño.
   3. Completar el diseño del atenuador.
4. Considere el diseño de un atenuador Pi$50\text{ dB}$ resistivo en un$75\:\Omega$ sistema. [Ejemplo de Parallels 5.5.1]
   1. Dibujar la topología del atenuador.
   2. Anote las ecuaciones de diseño.
   3. Completar el diseño del atenuador.
5. Un$20\text{ dB}$ atenuador en un$17\:\Omega$ sistema se corresponde idealmente tanto en la entrada como en la salida. Por lo tanto, no hay reflejos y la potencia entregada a la carga se reduce a$20\text{ dB}$ partir de la potencia aplicada. Si se aplica una$5\text{ W}$ señal al atenuador, ¿cuánta potencia se disipa en el atenuador?
6. Un atenuador Pi resistivo tiene resistencias de derivación$R_{1} = R_{2} = 294\:\Omega$ y una resistencia en serie$R_{3} = 17.4\:\Omega$. ¿Cuál es la atenuación (en decibelios) y la impedancia característica del atenuador?
7. Un atenuador Pi resistivo en un sistema con impedancia característica$Z_{0}$ tiene resistencias de derivación iguales$R_{1} = R_{2}$ y una resistencia en serie$R_{3}$. Mostrar eso$Z_{0} = \sqrt{(R_{1}^{2}R_{3})/(2R_{1} + R_{3})}$ y el factor de atenuación$K = \sqrt{(R_{1} + Z_{0})/(R_{1} − Z_{0})}$. [Comience con la Ecuación (5.5.2).]
8. Diseñar un atenuador Pi resistivo con una atenuación de$10\text{ dB}$ en un$100\:\Omega$ sistema.
9. Diseñar un atenuador Pi$3\text{ dB}$ resistivo en un$50\:\Omega$ sistema.
10. Un atenuador Pi resistivo tiene resistencias de derivación$R_{1} = R_{2} = 86.4\:\Omega$ y una resistencia en serie$R_{3} = 350\:\Omega$. ¿Cuál es la atenuación (en decibelios) y la impedancia del sistema del atenuador?
11. Derive los parámetros de$50\:\Omega$ dispersión del transformador ideal que se muestra a continuación donde el número de devanados en el lado secundario (Puerto$\mathsf{2}$) es el doble del número de devanados en el lado primario (Puerto$\mathsf{1}$).

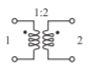
Figura$\PageIndex{1}$

1. ¿Qué es$S_{11}$? [Pista: Terminar puerto$\mathsf{2}$$50\:\Omega$ y determinar el coeficiente de reflexión de entrada.]
2. ¿Qué es$S_{21}$?
3. ¿Qué es$S_{22}$?
4. ¿Qué es$S_{12}$?

12. Derive los parámetros de$50\:\Omega$ dispersión de dos puertos del transformador magnético a continuación. El primario (Puerto$\mathsf{1}$) tiene$10$ giros, el secundario (Puerto$\mathsf{2}$) tiene$25$ giros.

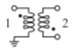
Figura$\PageIndex{2}$

1. ¿Qué es$S_{11}$?
2. ¿Qué es$S_{21}$?
3. ¿Qué es$S_{22}$?
4. ¿Qué es$S_{12}$?

13. Un híbrido de cuadratura ideal tiene los parámetros de dispersión
    $$S_{90^{\circ}}=\frac{1}{\sqrt{2}}\left[\begin{array}{cccc}{0}&{-\jmath}&{1}&{0}\\{-\jmath}&{0}&{0}&{1}\\{1}&{0}&{0}&{-\jmath}\\{0}&{1}&{-\jmath}&{0}\end{array}\right]\nonumber$$
    Dibuja el gráfico de flujo de señal del híbrido, etiquetando cada uno de los bordes y asignando$a_{1},\: b_{1},$ etc., a los nodos. (No comience con el SFG de una red genérica de 4 puertos.)
14. Un$180^{\circ}$ híbrido ideal tiene los parámetros de dispersión
    $$S_{180^{\circ}}=\frac{1}{\sqrt{2}}\left[\begin{array}{cccc}{0}&{1}&{-1}&{0}\\{1}&{0}&{0}&{1}\\{-1}&{0}&{0}&{1}\\{0}&{1}&{1}&{0}\end{array}\right]\nonumber$$
    Dibuja el gráfico de flujo de señal del híbrido, etiquetando cada uno de los bordes y asignando$a_{1},\: b_{1},$ etc., a los nodos. (Tenga en cuenta que no comience con el SFG de una red genérica de 4 puertos.)
15. Se aplica una señal a Puertos$\mathsf{2}$ y$\mathsf{3}$ de un$180^{\circ}$ híbrido, como se muestra en la Figura 5.8.2 (b). Si la señal consiste en un componente diferencial$0\text{ dBm}$ y un componente de modo común de$10\text{ dBm}$:
    1. Determinar la potencia entregada en Puerto$\mathsf{1}$.
    2. Determinar la potencia entregada en Puerto$\mathsf{4}$. Supongamos que el híbrido no tiene pérdidas.
16. Los RFIC de silicio utilizan trayectorias de señal diferenciales para minimizar la introducción de ruido de sustrato. Además, los amplificadores diferenciales son una topología óptima en circuitos polarizados en corriente. Las señales fuera del chip suelen estar en líneas de microcinta y por lo tanto la fuente y la carga, al estar fuera del chip, no son diferenciales. Los circuitos fuera del chip se denominan entonces de extremo único. Usando$180^{\circ}$ híbridos, diagramas y explicaciones, describa una arquitectura de sistema que se acomode a este entorno diferencial mixto y de un solo extremo.
17. Considera el híbrido que se muestra en la siguiente figura. Si el número de devanados de Bobinas$\mathsf{2}$ y$\mathsf{3}$ son dos veces el número de devanados de Bobina$\mathsf{1}$, muéstrelo para operación híbrida coincidente$2Z_{2} = Z_{3} = 8Z_{0}$.

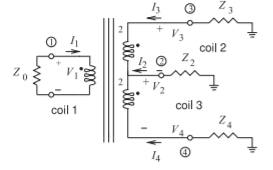
Figura$\PageIndex{3}$

18. El balun de la Figura 5.9.3 transforma un sistema desequilibrado con una impedancia de sistema de$Z_{0}$ a un sistema equilibrado con una impedancia de$4Z_{0}$. La transformación de impedancia real está determinada por el número de devanados de las bobinas. Diseñar un balun del tipo mostrado en la Figura 5.9.3 que transforme un$50\:\Omega$ sistema desequilibrado en un$377\:\Omega$ sistema equilibrado. [Pista: Encuentra la relación de los devanados de las bobinas.]
19. Un balun se puede realizar usando un transformador de alambre enrollado, y al cambiar el número de devanados en el transformador es posible lograr la transformación de impedancia, así como la funcionalidad balanceada a desequilibrada. Se requiere$500\text{ MHz}$ un balun basado en un transformador magnético para lograr la transformación de impedancia de una impedancia desequilibrada de$50\:\Omega$ a una impedancia equilibrada de$200\:\Omega$. Si hay$20$ devanados en el puerto balanceado del transformador de balun, ¿cuántos devanados hay en el puerto desequilibrado del balun?
20. Diseñe un divisor de potencia bidireccional de elementos agrupados en un$75\:\Omega$ sistema en$1\text{ GHz}$. Base tu diseño en un divisor de potencia Wilkinson.
21. Diseñe un divisor de potencia de tres vías en un$75\:\Omega$ sistema. Base tu diseño en un divisor de potencia Wilkinson usando líneas de transmisión e indica longitudes en términos de longitudes de onda.
22. Diseñe un divisor de potencia de tres vías de elementos agrupados en un$75\:\Omega$ sistema en$1\text{ GHz}$. Base tu diseño en un divisor de potencia Wilkinson.
23. Un divisor de potencia resistiva es un dispositivo de tres puertos que toma entrada de energía en Port$\mathsf{1}$ y entrega energía en Puertos$\mathsf{2}$ y$\mathsf{3}$ que son iguales; es decir,$S_{21} = S_{31}$. No obstante, la suma de la potencia en Puertos$\mathsf{2}$ y no$\mathsf{3}$ será igual a la potencia de entrada debido a la pérdida. Diseñe un divisor de potencia$75\:\Omega$ resistivo de tres puertos con entradas coincidentes,$S_{11} =0= S_{22} = S_{33}$. Es decir, dibujar el circuito resistivo y calcular sus valores de elementos.
24. Diseñar un balun basado en un transformador magnético si la carga equilibrada es$300\:\Omega$ y la impedancia desequilibrada es$50\:\Omega$.
    1. Dibuja el esquema del balun con la carga e indica la relación de devanados.
    2. Si el número de devanados en el lado desequilibrado del transformador es$20$, ¿cuántos devanados hay en el lado desequilibrado?
25. Desarrollar el diseño eléctrico de un híbrido rata-raza$30\text{ GHz}$ en un$50\:\Omega$ sistema.
26. Desarrollar el diseño eléctrico de un híbrido rata-raza$30\text{ GHz}$ en un$100\:\Omega$ sistema.
27. Diseñe un$180^{\circ}$ híbrido de elementos grumosos$1900\text{ MHz}$ usando$1\text{ nH}$ inductores.
28. Diseñe un híbrido de$90^{\circ}$ elementos grumosos$1900\text{ MHz}$ usando$1\text{ nH}$ inductores.
29. Diseñe un híbrido de$90^{\circ}$ elementos grumosos$500\text{ MHz}$ para un$75\:\Omega$ sistema.
30. Diseñe un$180^{\circ}$ híbrido de elementos grumosos en impedancias$1900\text{ MHz}$ coincidentes con la$50\:\Omega$ fuente y la carga.

5.16.1 Ejercicios por Sección

$†$desafiante,$‡$ muy desafiante

$§5.1\: 1$

$§5.2\: 2, 3, 4, 5$

$§5.5\: 6†, 7†, 8, 9, 10†$

$§5.8\: 11†, 12†$

$§5.9\: 13†, 14†, 15†, 16†, 17‡$

$§5.10\: 18†, 19†$

$§5.11\: 20†, 21†, 22†$

$§5.12\: 23†$

$§5.13\: 24‡, 25†, 26†, 27, 28, 29, 30$

5.16.2 Respuestas a ejercicios seleccionados

2. $12.57$
3. $R_{1}=R_{2}=74.5\:\Omega$
4. $75.48\:\Omega$
5. $4.95\text{ W}$

11. c)$0.6$
12. $-0.6897$

15. $10\text{ dBm}$

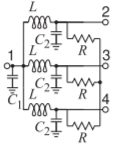
Figura$\PageIndex{4}$

$L=20.7\text{ nH}$,$C_{1}=3.68\text{ pF}$

$C_{2}=1.23\text{ pF}$,$R=75\:\Omega$

24. relación de devanados es$2.45$

30. Fig 5.13.3 (a)
    $L=5.92\text{ nH}$,$C=1.19\text{ pF}$