5.8: Transformador Magnético
- Page ID
- 80807
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección se discutirá el uso de transformadores magnéticos en circuitos de microondas. Los transformadores magnéticos se pueden usar directamente hasta unos pocos cientos de megahercios más o menos, pero las mismas propiedades de transformación se pueden lograr usando líneas de transmisión acopladas.
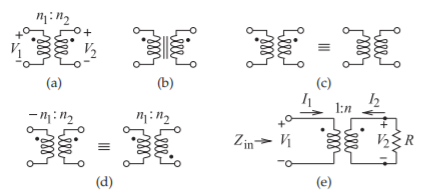
Figura\(\PageIndex{1}\): Transformadores magnéticos: (a) un transformador como dos devanados acoplados magnéticamente con\(n_{1}\) devanados en el primario (a la izquierda) y\(n_{2}\) devanados en el secundario (a la derecha) (los puntos indican polaridad magnética para que los voltajes\(V_{1}\) y\(V_{2}\) tengan el mismo signo ); (b) un transformador magnético con núcleo magnético; (c) representaciones idénticas de un transformador magnético con la polaridad magnética implicada para el transformador a la derecha; (d) dos representaciones equivalentes de un transformador que tiene polaridades magnéticas opuestas (un transformador inversor); y (e) un circuito transformador magnético.
5.8.1 Propiedades de un Transformador Magnético
Un transformador magnético (ver Figura\(\PageIndex{1}\)) acopla magnéticamente la corriente en un cable a la corriente en otro. El efecto se amplifica utilizando bobinas de alambres y utilizando un núcleo de material magnético (material con alta permeabilidad) para crear una mayor densidad de flujo magnético. Cuando se utilizan bobinas, se utiliza el símbolo que se muestra en la Figura\(\PageIndex{1}\) (a), con uno de los devanados llamado devanado primario y el otro llamado devanado secundario. Si hay un núcleo magnético alrededor del cual se enrollan las bobinas, entonces se utiliza el símbolo que se muestra en la Figura\(\PageIndex{1}\) (b), con las líneas verticales indicando el núcleo. Sin embargo, incluso si hay un núcleo, el símbolo de transformador más simple en la Figura\(\PageIndex{1}\) (a) se usa más comúnmente. Los núcleos magnéticos son útiles hasta varios cientos de megahercios y se basan en la alineación de dipolos magnéticos en el material del núcleo. Por encima de unos pocos cientos de megahercios los dipolos magnéticos no pueden reaccionar lo suficientemente rápido y así el núcleo parece un circuito abierto al flujo magnético. Por lo tanto, el núcleo no es útil para acoplar magnéticamente señales por encima de unos pocos cientos de megahercios. Como se mencionó, los puntos por encima de las bobinas en la Figura\(\PageIndex{1}\) (a) indican la polaridad del flujo magnético con respecto a las corrientes en las bobinas de manera que, como se muestra,\(V_{1}\) y\(V_{2}\) tendrán el mismo signo. Incluso si la polaridad magnética no se muestra específicamente, está implícita (ver Figura\(\PageIndex{1}\) (c)). Existen dos formas de mostrar la inversión de la polaridad magnética, como se muestra en la Figura\(\PageIndex{1}\) (d), donde un número negativo de devanados indica polaridad magnética opuesta.
El interés en el uso de transformadores magnéticos en el diseño de circuitos de alta frecuencia es que las configuraciones de transformadores magnéticos se pueden realizar utilizando líneas de transmisión acopladas para extender la operación a cientos de gigahercios. El transformador es fácil de conceptualizar, por lo que es conveniente desarrollar primero un circuito usando el transformador y luego traducirlo a forma de línea de transmisión.
Es decir, en el diseño de microondas “detrás del sobre”, se pueden utilizar transformadores para indicar el acoplamiento, quedando los detalles del acoplamiento hasta más tarde cuando el diseño eléctrico se traduce en un diseño físico. Se deben seguir las restricciones ya que no todas las configuraciones de transformadores pueden traducirse de esta manera. Las características del transformador se desarrollan a continuación.
Se utiliza la siguiente notación con un transformador magnético:
\(L_{1},\: L_{2}\): las autoinductancias de las dos bobinas
\(M\): la inductancia mutua
\(k\): el factor de acoplamiento,
\[\label{eq:1}k=\frac{M}{\sqrt{L_{1}L_{2}}} \]
Haciendo referencia a la Figura\(\PageIndex{1}\) (e), la relación del transformador de voltaje es
\[\label{eq:2}V_{2}=nV_{1} \]
donde\(n\) es la relación entre el número de devanados secundarios a primarios. Un transformador ideal tiene “acoplamiento perfecto”, indicado por\(k = 1\), y las autoinductancias son proporcionales al cuadrado del número de devanados, por lo que
\[\label{eq:3}\frac{V_{2}}{V_{1}}=\sqrt{\frac{L_{2}}{L_{1}}} \]
La ecuación general que relaciona las corrientes del circuito en la Figura\(\PageIndex{1}\) (e) es
\[\label{eq:4} RI_{2} +\jmath\omega L_{2}I_{2} + \jmath\omega MI_{1} = 0 \]
y así
\[\label{eq:5}\frac{I_{1}}{I_{2}}=-\frac{R+\jmath\omega L_{2}}{\jmath\omega M} \]
Si\(R ≪ \omega L_{2}\), entonces la relación del transformador de corriente es
\[\label{eq:6}\frac{I_{1}}{I_{2}}\approx -\frac{L_{2}}{M}=-\sqrt{\frac{L_{2}}{L_{1}}} \]
Observe que la combinación de Ecuaciones\(\eqref{eq:3}\) y\(\eqref{eq:6}\) lleva al cálculo del efecto transformador sobre la impedancia. En el\(\mathsf{1}\) lado de la bobina, la impedancia de entrada es (refiriéndose a la Figura 5-19 (e))
\[\label{eq:7}Z_{\text{in}}=\frac{V_{1}}{I_{1}}=-\frac{V_{2}}{I_{2}}\left(\frac{L_{1}}{L_{2}}\right)=R\frac{L_{1}}{L_{2}} \]
En la práctica, sin embargo, siempre hay alguna fuga de campo magnético, no todo el campo magnético creado por la corriente en la bobina\(\mathsf{1}\) pasa a través (o enlaces) de la bobina\(\mathsf{2}\), y así\(k < 1\). Luego de Ecuaciones\(\eqref{eq:3}\) —\(\eqref{eq:7}\),
\[\begin{align}\label{eq:8}V_{1}&=\jmath\omega L_{1}I_{1}+\jmath\omega I_{2}\\ \label{eq:9}0&=RI_{2}+\jmath\omega L_{2}I_{2}+\jmath\omega MI_{1}\end{align} \]
Nuevamente, suponiendo que\(R ≪ \omega L_{2}\), se obtiene una expresión modificada para la impedancia de entrada que da cuenta del acoplamiento no ideal:
\[\label{eq:10}Z_{\text{in}}=R\frac{L_{1}}{L_{2}}+\jmath\omega L_{1}(1-k^{2}) \]
El acoplamiento imperfecto,\(k < 1\), hace que la impedancia de entrada sea reactiva y esto limita el ancho de banda del transformador. La capacitancia parásita es otro factor que impacta el ancho de banda del transformador.
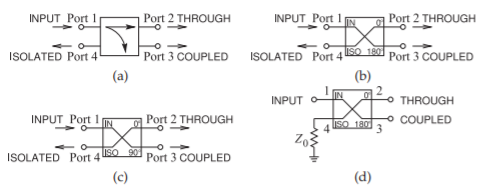
Figura\(\PageIndex{2}\): Símbolos de uso común para híbridos: (a) puertos pasantes y acoplados; (b)\(180^{\circ}\) híbrido; (c)\(90^{\circ}\) híbrido; y (d) híbrido con el puerto aislado terminado en una carga emparejada.

