6.3: Redes de transformación de impedancia

Los transformadores y elementos reactivos considerados en esta sección pueden ser utilizados para transformar sin pérdidas los niveles de impedancia. el suyo es un aspecto básico del diseño de redes.

6.3.1 El Transformador Ideal

El transformador ideal que se muestra en la Figura 6.2.2 se puede utilizar para hacer coincidir una carga con una fuente si las impedancias de fuente y carga son resistencias. Esto se mostrará comenzando con las relaciones constitutivas del transformador:

\[\label{eq:1}V_{1}=nV_{2}\quad\text{and}\quad I_{1}=-I_{2}/n \]

Aquí\(n\) está la relación del transformador. Para un transformador de alambre enrollado,\(n\) es la relación entre el número de devanados en el lado primario, Puerto\(\mathsf{1}\), al número de devanados en el lado secundario, Puerto\(\mathsf{2}\). Así la resistencia de entrada,\(R_{\text{in}}\), está relacionada con la resistencia de carga,\(R_{L}\), por

\[\label{eq:2}R_{\text{in}}=\frac{V_{1}}{I_{1}}=-n^{2}\frac{V_{2}}{I_{2}}=n^{2}R_{L} \]

El problema de coincidencia con las impedancias puramente resistivas de carga y fuente se resuelve eligiendo la relación de bobinado adecuada,\(n\). Sin embargo, los problemas solo resistivos son raros en RF, por lo que se deben usar otros circuitos coincidentes.

6.3.2. Elemento reactivo de la serie A

El emparejamiento mediante elementos agrupados se basa en las propiedades de transformación de impedancia y admitancia de elementos reactivos en serie y derivación. Incluso un solo elemento reactivo puede lograr una adaptación de impedancia limitada. Considere el elemento reactivo en serie que se muestra en la Figura\(\PageIndex{1}\) (a). Aquí el elemento reactivo\(X_{S}\),

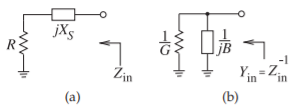
Figura\(\PageIndex{1}\): Coincidencia usando una reactancia en serie: (a) el elemento reactivo en serie; y (b) su circuito de derivación equivalente.

está en serie con una resistencia\(R\). El equivalente de derivación de esta red se muestra en la Figura\(\PageIndex{1}\) (b) con una susceptancia de derivación de\(B\). En esta transformación la resistencia se\(R\) ha convertido en una resistencia\(R_{P} = 1/G\). Las matemáticas que describen esta transformación son las siguientes. La admitancia de entrada de la conexión en serie (Figura\(\PageIndex{1}\) (a)) es

\[\label{eq:3}Y_{\text{in}}(\omega)=\frac{1}{Z_{\text{in}}(\omega)}=\frac{1}{R+\jmath X_{S}}=\frac{R}{R^{2}+X_{S}^{2}}-\jmath\frac{X_{S}}{R^{2}+X_{S}^{2}} \]

Así, los elementos de la red de derivación equivalente, Figura\(\PageIndex{1}\) (b), son

\[\label{eq:4}G=\frac{R}{R^{2}+X_{S}^{2}}\quad\text{and}\quad B=-\frac{X_{S}}{R^{2}+X_{S}^{2}} \]

La “resistencia” de la red,\(R\), se ha transformado a un nuevo valor,

\[\label{eq:5}R_{P}=G^{-1}=\frac{R^{2}+X_{S}^{2}}{R}>R \]

Este es un comienzo importante para el emparejamiento, ya que se\(X_{S}\) puede elegir para convertir\(R\) (una carga, por ejemplo) a cualquier valor de resistencia deseado (como la resistencia de una fuente). Sin embargo, todavía hay una reactancia residual que debe eliminarse para completar el diseño de la red coincidente. Antes de pasar a la solución de este problema consideremos el siguiente ejemplo.

Ejemplo\(\PageIndex{1}\): Capacitive Impedance Transformation

Considere las propiedades de transformación de impedancia del elemento capacitivo serie en la Figura\(\PageIndex{2}\) (a). Demuestre que el condensador se puede ajustar para obtener cualquier resistencia de derivación positiva.

Solución

El concepto aquí es que la red de resistencias y condensadores en serie tiene un circuito de derivación equivalente que incluye un condensador y una resistencia. Al ajustar\(C_{S}\) cualquier valor se puede obtener para\(R_{P}\). A partir de la ecuación\(\eqref{eq:5}\),

\[\label{eq:6}R_{P}=\frac{R_{0}^{2}+(1/\omega^{2}C_{S}^{2})}{R_{0}}=\frac{1+\omega^{2}C_{S}^{2}R_{0}^{2}}{\omega^{2}C_{S}^{2}R_{0}} \]

y la susceptancia es

\[\label{eq:7}B=\frac{(1/\omega C_{S})}{R_{0}^{2}+1/\omega^{2}C_{S}^{2}}=\omega\frac{C_{S}}{1+\omega^{2}C_{S}^{2}R_{0}^{2}} \]

Por lo tanto

\[\label{eq:8}C_{P}=\frac{B}{\omega}=\frac{C_{S}}{1+\omega^{2}C_{S}^{2}R_{0}^{2}} \]

\(R_{0}\)Para hacer coincidir con una carga resistiva\(R_{P}\)\((> R_{0})\) a una frecuencia de radián\(\omega_{d}\), entonces, a partir de la Ecuación\(\eqref{eq:6}\), la capacitancia en serie requerida, es decir, la ecuación de diseño para\(C_{S}\), proviene de

\[\label{eq:9}\omega_{d}C_{S}=1/\sqrt{R_{0}R_{P}-R_{0}^{2}} \]

Para completar el diseño coincidente, use un inductor de derivación\(L\), como se muestra en la Figura\(\PageIndex{2}\) (c), donde\(\omega_{d}C_{P} = 1/(\omega_{d}L)\). La impedancia equivalente en la Figura\(\PageIndex{2}\) (c) es una resistencia de valor\(R_{P}\), con un valor que se puede ajustar eligiendo\(C_{S}\) cuál luego requiere\(L\) ser ajustado.

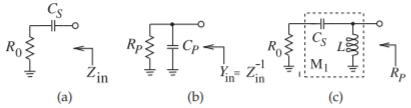
Figura\(\PageIndex{2}\): Transformación de impedancia por un elemento reactivo en serie: (a) una resistencia con un condensador en serie; (b) su circuito de derivación equivalente; y (c) una\(LC\) red.

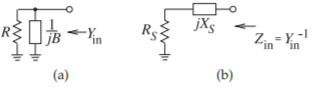
Figura\(\PageIndex{3}\): Una resistencia con (a) un elemento reactivo paralelo en derivación donde\(B\) es una susceptancia, y (b) su circuito en serie equivalente.

6.3.3 Un Elemento Reactivo Paralelo

El procedimiento dual del emparejamiento en serie es el uso de un elemento reactivo paralelo, como se muestra en la Figura\(\PageIndex{3}\) (a). La admitancia de entrada del circuito de derivación

\[\label{eq:10}Y_{\text{in}}=\frac{1}{R}+\jmath B \]

Esto se puede convertir en un circuito en serie calculando\(Z_{\text{in}} = 1/Y_{\text{in}}\):

\[\label{eq:11}Z_{\text{in}}=\frac{R}{1+\jmath BR}=\frac{R}{1+B^{2}R^{2}}-\jmath\frac{BR^{2}}{1+B^{2}R^{2}} \]

Entonces

\[\label{eq:12}R_{S}=\frac{R}{1+B^{2}R^{2}}\quad\text{and}\quad X_{S}=\frac{-BR^{2}}{1+B^{2}R^{2}} \]

Observe eso\(R_{S}<R\).

Ejemplo\(\PageIndex{2}\): Parallel Tuning

Como ejemplo del uso de un elemento reactivo paralelo para sintonizar un valor de resistencia, considere el circuito de la Figura 6.4.1 (a) donde un condensador sintoniza el valor de resistencia efectivo para que el circuito equivalente en serie (Figura 6.4.1 (b)) tenga elementos

\[\label{eq:13}R_{S}=\frac{R_{0}}{1+\omega^{2}C_{P}^{2}R_{0}^{2}}\quad\text{and}\quad X_{S}=-\frac{\omega C_{P}R_{0}^{2}}{1+\omega^{2}C_{P}^{2}R_{0}^{2}}=-\frac{1}{\omega C_{S}} \]

Entonces

\[\label{eq:14}C_{S}=\frac{1+\omega^{2}C_{P}^{2}R_{0}^{2}}{\omega^{2}C_{P}R_{0}^{2}} \]

Ahora considere\(R_{0}\) hacer coincidir con una carga resistiva\(R_{S}\), que es menor que\(R_{0}\) a una frecuencia dada ωd. Esto requiere que

\[\omega_{d}C_{P}=\sqrt{1/(R_{S}R_{0})-1/R_{0}^{2}}\nonumber \]

Para completar el diseño, utilice un inductor en serie para eliminar el efecto reactivo del condensador, como se muestra en la Figura 6.4.1 (C). El valor del inductor requerido se encuentra a partir de

\[\label{eq:15}\omega_{d}L=\frac{1}{\omega_{d}C_{s}},\quad\text{that is,}\quad L=\frac{1}{\omega_{d}^{2}C_{S}} \]